- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание для самостоятельной работы № 2
Федеральное государственное бюджетное образовательное учреждение высшего образования «Чувашский государственный университет им. И.Н. Ульянова»
Кафедра вычислительной техники
Расчетно-графическая работа
по дисциплине Информатика
Вариант 11
Выполнил: Карпов К.Э.
студент группы ИВТ-41-20
Проверила: ст. преп.
Первова Н.В.
Чебоксары, 2020
Задание для самостоятельной работы № 2
2. Переведем числа 72 и 113 из десятичной СС в двоичную. Далее запишем результат в прямом коде и переведем его в дополнительны й.
; 
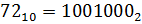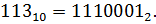
Если 72 = Y, 113 = X, то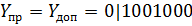 
и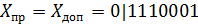 
, т.к. 72 > 0 и 113 > 0.
Также переведем число, обратное числу Y в дополнительный код. Это число нужно для дальнейшего деления.
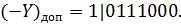
Произведем деление Y на X в машинном коде. Возьмем разрядную сетку n=8. Проведем проверку на переполнение (I). Если переполнения нет, переходим к самому процессу деления (II).
| I. | 00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | |||
| Y0=1:Z=Z+X | + | 11 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||||
| R<0:OK | 11 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | |||
| II. ИП: R0=Xд. | 00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | |||
| R0<< | 1. | 00 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | - | ||
| R1=R0-Yд*2^7 | + | 11 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||||
| R1<0; Z6=0 | 11 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |||
| R1=R1+Yд*2^7 | + | 00 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |||||||||
| 00 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | ||||
| R1<< | 2. | 00 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | - | ||
| R2=R1-Yд*2^7 | + | 11 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||||
| R2<0; Z5=0 | 11 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | |||
| R2=R2+Yд*2^7 | + | 00 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |||||||||
| 00 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | ||||
| R2<< | 3. | 00 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | - | ||
| R3=R2-Yд*2^7 | + | 11 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||||
| R3<0; Z4=0 | 11 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |||
| R3=R3+Yд*2^7 | + | 00 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |||||||||
| 00 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ||||
| R3<< | 4. | 00 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | - | ||
| R4=R3-Yд*2^7 | + | 11 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||||
| R4<0; Z3=0 | 11 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |||
| R4=R4+Yд*2^7 | + | 00 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |||||||||
| 00 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ||||
| R4<< | 5. | 00 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | - | ||
| R5=R4-Yд*2^7 | + | 11 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||||
| R5<0; Z2=0 | 11 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |||
| R5=R5+Yд*2^7 | + | 00 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |||||||||
| 00 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ||||
| R5<< | 6. | 00 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | - | ||
| R6=R5-Yд*2^7 | + | 11 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||||
| R6<0; Z1=0 | 11 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| R6=R6+Yд*2^7 | + | 00 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |||||||||
| 00 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| R6<< | 7. | 00 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | - | ||
| R7=R6-Yд*2^7 | + | 11 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||||
| R7>0; Z0=1 | 00 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Определяем знак результата. Так как знаки исходных операндов одинаковые, то знак результата будет положительным.
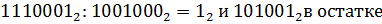
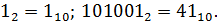
Ответ: Z=113/72=1 и 41 в ост..
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|