ПОДГОТОВИТЕЛЬНЫЕ ЗАДАНИЯ К АТТЕСТАЦИИ ( алгебра)

ПОДГОТОВИТЕЛЬНЫЕ ЗАДАНИЯ К АТТЕСТАЦИИ ( алгебра)

1. Дана функция f(x) = 4x–1. Найдите f(– 3) и нули функции.

2. Постройте график функции y= (x – 3)²– 2. Определите промежутки возрастания и убывания функции.

3. Решите уравнение:

а) 3х² – х³ = 0;

б) х⁴ – 7х² + 12 =0.

4. Решите неравенство:

а) (х+2)(х–1)(х– 4)≥ 0;

б) x²– 14x + 24 ≤ 0.

9 класс

Геометрия

Часть 1

1. В трапеции ABCF, основания которой равны 7 и 10 см, MN – средняя линия.

Отрезок BE параллелен стороне CF. Найдите длину отрезка MK.

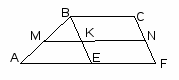
Ответ:__________________

2. 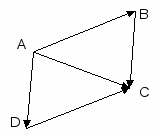Какие из равенств являются верными? Укажите в ответе их номера.

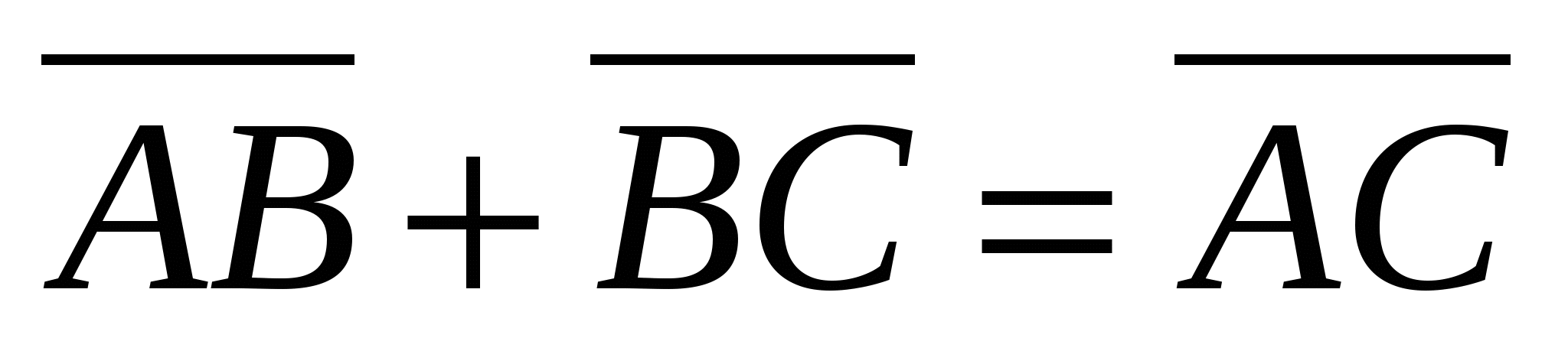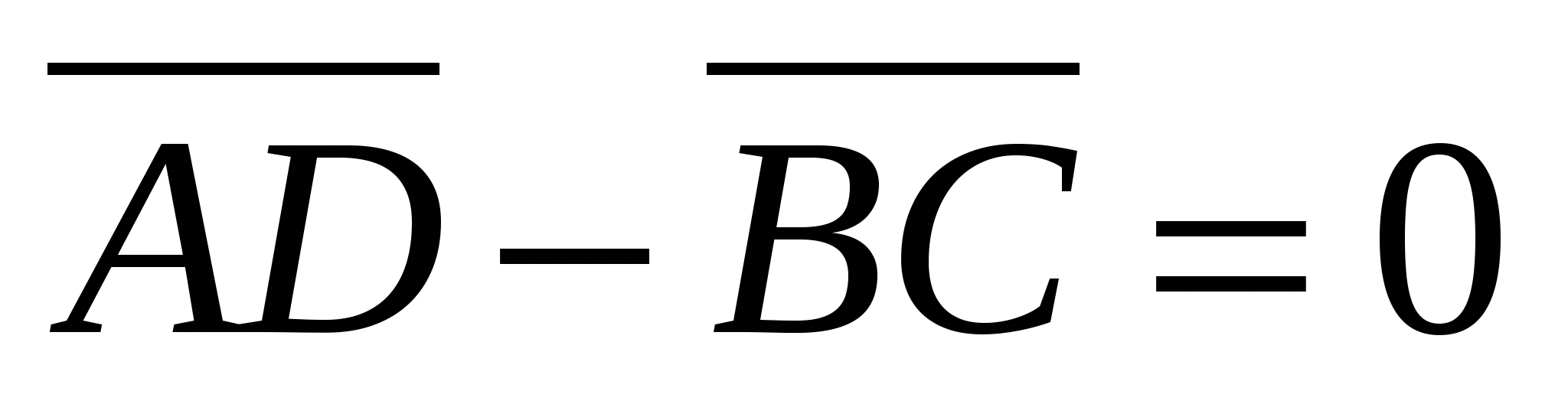1. 2. 3.

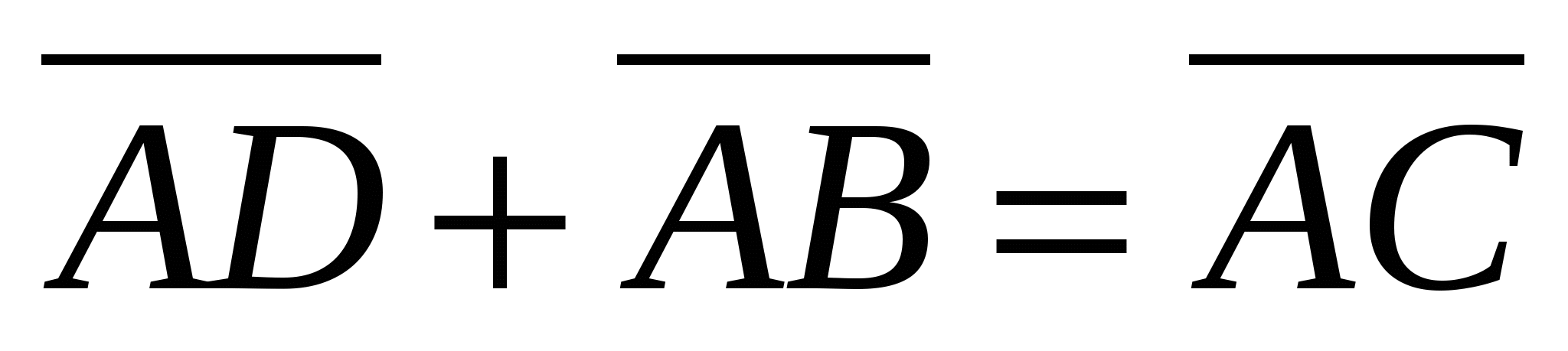
Ответ:__________________

3.Начертите два неколлинеарных вектора c и d. Постройте векторы, равные:

а) 3c +2d; б) c – 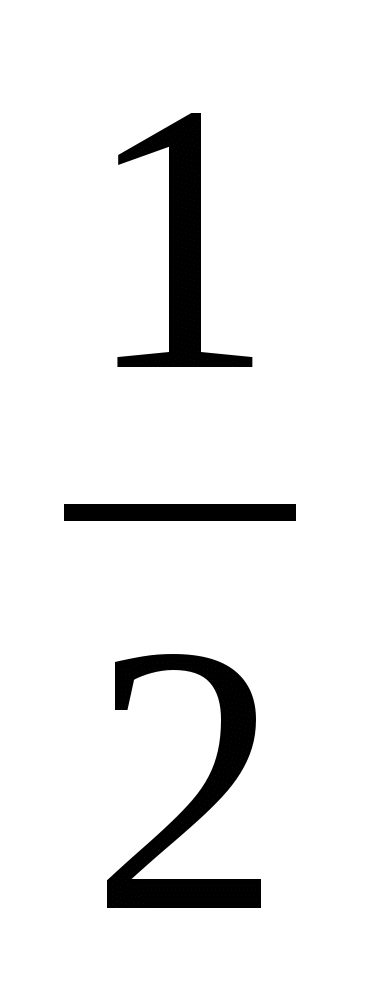d.

4.Даны векторы: b{-12;18}, a=2i+j, c=2a – 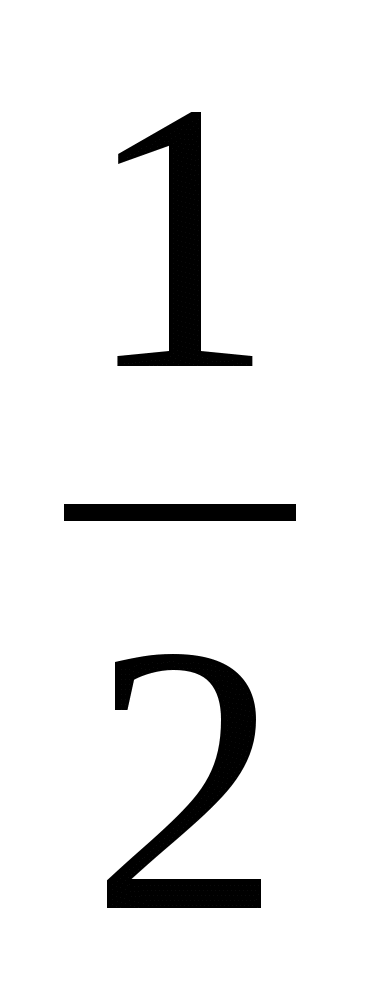b.Найдите координаты вектора с.

5.Даны векторы: b{-12;18}, a=2i+j, c=2a – 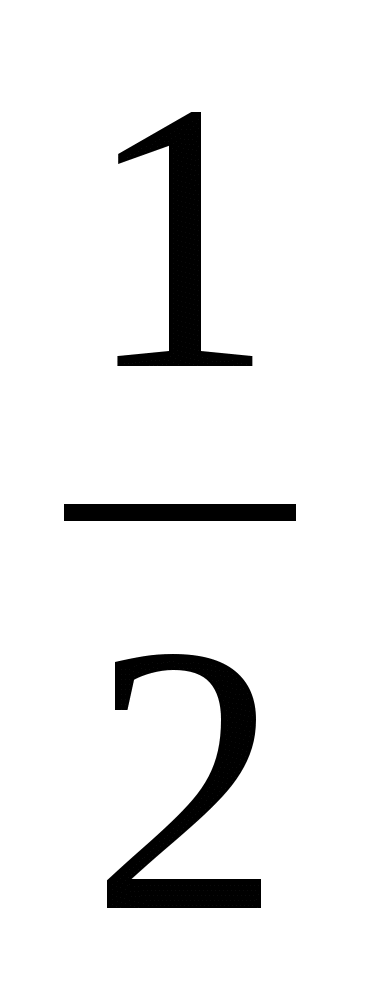b. Найдите длину вектора с.

6.Выберите верные утверждения, запишите их номера без пробелов и запятых:

1) От любой точки можно отложить вектор, равный данному и притом только один.

2) Векторы называются равными, если они сонаправлены

3) Средняя линия трапеции параллельна его основаниям и равна их полусумме

4) каждая координата суммы двух и более векторов равна разности соответствующих координат этих векторов.

5) Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

7.Найдите координаты центра окружности (х + 4)² + (у - 3)² = 9

Часть 2

(запишите подробное решение задач)

1.Напишите уравнение прямой, проходящей через две точки А(-3;-3) и В(3;5)

2.Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит среднюю линию на два отрезка, равные 2 см и 6 см. Найдите основания трапеции.