
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ. Расчет параметров и процессов идеального газа
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
На практических занятиях решаются задачи по основным разделам курса. Наибольшее внимание уделяется усвоению законов термодинамики и теплообмена, методам расчета и анализа процессов и циклов холодильных машин.
3.1. Расчет параметров и процессов идеального газа
Основными параметрами состояния являются: удельный объем, абсолютная температура, абсолютное давление.
Удельный объем v, м3/кг:
v =V/m = 1/ρ,
где V, м3 – объем, m, кг –масса, ρ, кг/м3 –плотность.
Абсолютная температура Т, К:
Т = 273,15 + t.
Абсолютное давление р, Па:
р = ратм + ризб,
р = ратм – рвак.
где: ратм – атмосферное давление,
ризб – избыточное давление,
рвак – вакуумное давление.
Связь между единицами измерения:
1кПа = 103 Па; 1МПа = 106 Па,
1бар = 105 Па = 100 кПа,
1ат = 1 кгс/см2 = 98000 Па = 98 кПа,
1мм. рт. ст. =133,3 Па.
В технической термодинамике рассматривают следующие основные термодинамические процессы:
изохорный – при постоянном объеме (v = const),
изобарный - при постоянном давлении (р = const),
изотермический – при постоянной температуре (Т = const),
адиабатный – без внешнего теплообмена (δq = 0),
политропный – при постоянной теплоемкости.
Характеристики, относящиеся к 1 кг вещества, называются удельными, они обозначаются строчными буквами, а характеристики, относящиеся к полной массе – заглавными. Полные характеристики получаются умножением удельных на величину массы:
Q =m∙q, L = m∙ℓ.
Уравнение состояния идеального газа:
p×v = R×T для 1 кг идеального газа;
p×V=m×R×T при расчетах с произвольной массой m,
где R, Дж/(кг×К) – удельная газовая постоянная (таблица 1 Приложения).
R=Rμ /μ = 8,31451×103/μ.
1 закон термодинамики: q = Δu + ℓ.
В таблице 1 приведены формулы для расчета процессов.
ТТаблица 1
| Процесс | Связь параметров | Работа изменения объема | Теплота |
| Изохор- ный | p2/p1 = T2/T1 | ℓ = 0 | q = cv (T2-T1) |
| Изобар- ный | v2/v1 = T2/T1 | ℓ = p (v2 -v1) | q = cp (T2-T1) |
| Изотер-мический | p2/p1 = v1/v2 | ℓ =RT ln (v2/v1) ℓ =RT ln (p1/p2) | q = ℓ |
| Адиабат-ный | р2/ р1 = (v1/v2)k T2/T1 = (v1/v2)k-1 T2/T1 = (р2/р1)(k-1)/k | ℓ= 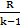 (T1-T2) (T1-T2)
| q = 0 |
| Политроп-ный | р2/ р1 = (v1/v2)n T2/T1 = (v1/v2)n-1 T2/T1 = (р2/р1)(n-1)/n | ℓ= 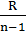 (T1-T2) (T1-T2)
| q = cv 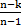 (T2-T1) (T2-T1)
|
Изменение внутренней энергии идеального газа в термодинамическом процессе:
Δu = cv∙(T2-Т1).
Изменение энтальпии идеального газа в термодинамическом процессе:
Δh = cp∙(T2-Т1).
Массовые теплоемкости идеального газа cp и cv можно определить по формулам:
cp = k·R/(k-1); cv = R/(k-1),
или как отношение мольной теплоёмкости газов к молекулярной массе (таблица 2 Приложения):
cv = mсv/m, cp= mcр/m ,
k = cp/cv - показатель адиабаты или коэффициент Пуассона.
Задачи
Задача 3.1.При температуре t1 = 20ºС 2 кг углекислоты сжимается изотермически до десятикратного уменьшения объема. Определить конечное давление р2, работу сжатия и отводимую теплоту, если начальное давление р1 =0,1 МПа. Принять, что газ идеальный.
Решение.
Конечное давление:
p2/p1 = V1/V2,
p2 = p1 (V1/V2) = 0,1∙(10/1) = 1,0 МПа.
Так как для идеального газа в изотермическом процессе нет изменения внутренней энергии, то по первому закону термодинамики теплота процесса равна работе:
L =Q =m∙R∙T ln (v2/v1).
L = 2∙189 ∙293 ln (1/10) = -254,6 кДж.
Задача 3.2.1 кг воздуха адиабатно расширяется от начального состояния с температурой t1 = 20ºС и давлением р1 =0,8 МПа до давления р2 =0,2 МПа. Определить параметры газа в конце расширения, работу процесса и изменение внутренней энергии газа.
Решение. Температура в конце адиабатного расширения:
T2 = T1 (р2/ р1)(k-1)/k = 293 (0,2/0,8)(1,4-1)/1,4 =198 К = - 75ºС.
Удельный объем воздуха в конце расширения:
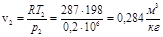 .
.
Работа адиабатного процесса:
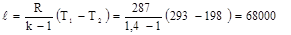 Дж/кг
Дж/кг
Изменение внутренней энергии:
∆u = u2 – u1 = -ℓ = - 68000 Дж/кг.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|