
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Порядок выполнения работы
 Цель работы: : определить центростремительное ускорение шарика под действием сил тяжести и упругости при его равномерном движении по окружности.
Цель работы: : определить центростремительное ускорение шарика под действием сил тяжести и упругости при его равномерном движении по окружности.
Оборудование:штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр лабораторный, весы с разновесами, шарик на нити, кусочек пробки с отверстием, лист бумаги, линейка.
Теория:Эксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиусом R. При этом нить АВ, к которой прикреплён шарик, описывает поверхность прямого кругового конуса. Из кинематических соотношений следует, что
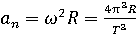
 На шарик действуют две силы: сила тяжести m
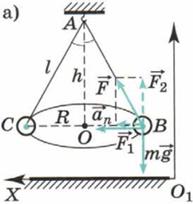
На шарик действуют две силы: сила тяжести m 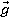 и сила натяжения нити
и сила натяжения нити 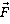 (рис. Л.1, а). Согласно второму закону Ньютона
(рис. Л.1, а). Согласно второму закону Ньютона 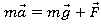 . Разложив силу
. Разложив силу 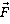 на составляющие
на составляющие 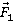 и
и 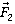 , направленные по радиусу к центру окружности и по вертикали вверх, второй закон Ньютона запишем следующим образом:
, направленные по радиусу к центру окружности и по вертикали вверх, второй закон Ньютона запишем следующим образом: 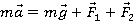 . Тогда можно записать: mап = F1. Отсюда аn =
. Тогда можно записать: mап = F1. Отсюда аn = 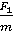 .
.
Модуль составляющей F1 можно определить, пользуясь подобием треугольников ОАВ и F1FB: Fl/R = mg/h ( 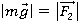 . Отсюда F1 = mgR/h и an = gR/h.
. Отсюда F1 = mgR/h и an = gR/h.
Сопоставим все три выражения для ап:
ап = 4 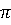 2R/T2, ап =gR/h, аn =
2R/T2, ап =gR/h, аn = 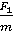
и убедимся, что числовые значения центростремительного ускорения, полученные тремя способами, примерно одинаковы.
Порядок выполнения работы
1.Определите массу шарика на весах с точностью до 1 г.
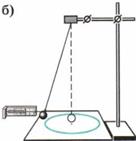 2. Нить проденьте сквозь отверстие в пробке и зажмите пробку в лапке штатива (рис. Л.2, б).
2. Нить проденьте сквозь отверстие в пробке и зажмите пробку в лапке штатива (рис. Л.2, б).
3.Начертите на листе бумаги окружность, радиус которой около 20 см. Измерьте радиус с точностью до 1 см.
4. Штатив с маятником расположите так, чтобы продолжение нити проходило через центр окружности.
5. Взяв нить пальцами у точки подвеса, вращайте маятник так, чтобы шарик описывал такую же окружность, как и начерченная на бумаге.
6. Отсчитайте время, за которое маятник совершает заданное число (например, в интервале от 30 до 60) оборотов.
7. Определите высоту конического маятника. Для этого измерьте расстояние по вертикали от центра шарика до точки подвеса (считаем h ≈ l).
8. Оттяните горизонтально расположенным динамометром шарик на рас стояние, равное радиусу окружности, и измерьте модуль составляющей 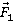 .
.
9. Повторите опыт несколько раз. Результаты измерений (в СИ) и вычислений занесите в таблицу:
| Номер опыта | R, м | N | ∆t, с | T=  с с
| h, м | m, кг | 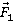 , Н , Н
|
| 1. | |||||||
| 2. | |||||||
| 3. | |||||||
| 4. | |||||||
| 5. | |||||||
| Среднее значение |
10. Используя среднее значение, найдите модуль центростремительного ускорения по формулам
ап = 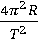 , ап =
, ап = 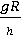 и аn =
и аn = 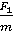
11. Результаты средних значений и вычислений занесите в таблицу .
| Номер опыта | R, м | N | ∆t, с | T=  с с
| h, м | m, кг | ап = 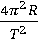 м/с2 м/с2
| ап = 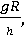 м/с2 м/с2
| аn = 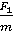 ,
м/с2 ,
м/с2
|
 12. Сравните полученные три значения модуля центростремительного ускорения и сделайте вывод.
12. Сравните полученные три значения модуля центростремительного ускорения и сделайте вывод.
Контрольные вопросы:
1. Какие силы действуют на шарик конического маятника при постоянном угле отклонения нити?
2. В данной работе мы рассматривали шарик как материальную точку. Всегда ли это возможно?
3. Выведите первую расчётную формулу: ап = 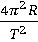 . Назовите все физические величины и единицы их измерений, использовавшиеся при выводе формулы.
. Назовите все физические величины и единицы их измерений, использовавшиеся при выводе формулы.
4. Какой закон применялся при выводе второй формулы: ап = 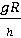 . Сформулируйте его.
. Сформулируйте его.
5. Объясните, как измеряют модуль составляющей 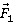 .при расчёте центростремительного ускорения по формуле аn =
.при расчёте центростремительного ускорения по формуле аn = 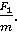
6. За счет чего получилось несовпадение значений ускорения, определенных разными способами?

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|