
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение квадратных неравенств с помощью метода интервала
Решение квадратных неравенств с помощью метода интервала
Автор: © 2015, OOO КОМПЭДУ, http://compedu.ru
Описание:
При поддержке проекта http://videouroki.net
Задание 1
Вопрос:
Выберите формулы, с помощью которых можно квадратный трехчлен разложить на множители:
Выберите несколько из 3 вариантов ответа:
1)  где
где 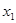 и
и 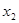 - корни соответствующего квадратного уравнения.
- корни соответствующего квадратного уравнения.
2) 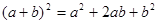
3) 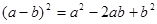
Задание 2
Вопрос:
Найдите сумму наибольшего целого отрицательного и наименьшего целого положительного решений неравенства:
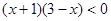 .
.
Запишите число: ___________________________
Задание 3
Вопрос:
При решении неравенства получили следующие промежутки, на которых функция принимает значения одного знака (см. рисунок). Укажите промежутки, которые будут решениями неравенства f(x)>0:
Изображение:

Выберите несколько из 4 вариантов ответа:
1) 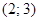 2)
2) 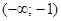 3)
3) 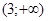 4)
4) 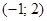
Задание 4
Вопрос:
При решении неравенства получили следующие промежутки, на которых функция принимает значения одного знака (см. рисунок). Укажите промежутки, которые будут решениями неравенства f(x)<0:
Изображение:

Выберите несколько из 3 вариантов ответа:
1) 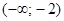 2)
2) 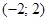 3)
3) 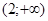
Задание 5
Вопрос:
Укажите наименьшее положительное целое число, которое является решением неравенства 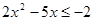 .
.
Запишите число: ___________________________
Задание 6
Вопрос:
Укажите многочлен, который произведением двух множителей можно представить так: 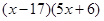 .
.
Выберите один из 4 вариантов ответа:
1) 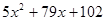 2)
2) 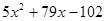 3)
3) 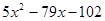 4)
4) 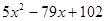
Задание 7
Вопрос:
При решении неравенства получили следующие промежутки, на которых функция принимает значения одного знака (см. рисунок). Укажите промежутки, которые будут решениями неравенства: 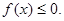
Изображение:

Выберите несколько из 6 вариантов ответа:
1) 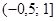 2)
2) 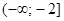 3)
3) 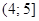 4)
4) 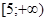 5)
5) 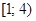 6)
6) 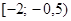
Задание 8
Вопрос:
Выберите множители, на которые можно разложит многочлен: 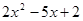 .
.
Выберите несколько из 4 вариантов ответа:
1) (x-2) 2) (2x+1) 3) (2x-1) 4) (x+2)
Задание 9
Вопрос:
Выберите множители, на которые можно разложит многочлен: 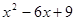 .
.
Выберите несколько из 4 вариантов ответа:
1) (x+2) 2) (x-3) 3) (2x+1) 4) (x-3)
Задание 10
Вопрос:
Выберите множители, на которые можно разложит многочлен:  .
.
Выберите несколько из 4 вариантов ответа:
1) (x-4) 2) (x+4) 3) (5x-2) 4) (5x+2)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|