
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Экзаменационная программа по математическому анализу 1 семестр
Экзаменационная программа по математическому анализу 1 семестр
2016-2017 г.
1. Основные понятия о множествах. Операции над множествами.
2. Числовые множества. Числовая прямая. Основные числовые промежутки.
3. Принцип минимального числа. Принцип математической индукции.
4. Неравенство Коши и Бернулли.
5. Аксиома полноты действительных чисел. Бином Ньютона.
6. Принцип Архимеда. Теорема о существовании целой части числа.
7. Ограниченные множества. Верхняя и нижняя грани множеств. Теорема Вейерштрасса. Абсолютная величина.
8. Метрические и арифметические пространства. Теорема о вложенных отрезках.
9. Общее понятие функции (инъективное, сюрьективное и биективное отображения). Частные случаи функций.
10. Счетные и равномощные множества, теорема о счетном множестве действительных чисел на отрезке [0,1].
11. Числовые последовательности. Предел последовательности, ограниченные и неограниченные последовательности.
12. Теорема о единственности предела. Теорема о локальности предела последовательности.
13.Теорема о сохранение неравенств. Теорема о необходимом условии существования конечного предела последовательности.Бесконечный предел последовательности, бесконечно большие последовательности, бесконечно малые последовательности.
14. Свойства пределов связанных с арифметическими операциями над последовательностями.
15. Теоремы об ограниченности обратной последовательности, о связи между пределами сходящейся и бесконечно малой последовательностей.
16. Свойства бесконечно малых последовательностей. Связь бесконечно малой с бесконечно большой последовательностью.
17. Теоремы об умножении сходящихся последовательностей и о делении сходящихся последовательностей.
18. Оценочный признак существования предела. Переход к пределу в неравенствах.
19. Предел монотонной последовательности. Неперово число (число е).
20. Частные пределы. Теорема Больцано - Вейерштрасса (без доказательства).
21. Критерий Коши. Необходимое и достаточное условие существования конечного предела.
22. Эквивалентные последовательности. Свойства эквивалентных последовательностей.
23. Предел комплексной последовательности.
24. Предел и непрерывность функции. Окрестность и ее свойства. Аксиома отделимости Хаусдорфа. Проколотые окрестности.
25. Предельная точка множества. Теоремы Больцано - Вейерштрасса (без доказательства) о выделении конечного покрытия (без доказательства). Предел функции.
26. Определение предела функции по Гейне. Теорема об эквивалентности определений.
27. Односторонние пределы. Теорема о локальности функции имеющих предел.
30. Теорема о связи функции имеющей предел с бесконечно малой. Необходимое и достаточное условие существования предела функции.
31. Свойства пределов связанные с арифметическими действиями над функциями.
32. Свойства пределов связанные с неравенствами над функциями. Оценочный признак существования предела функции в точке.
33. Теорема о пределе сложной функции. Свойства бесконечно малых функций.
34. Замечательные пределы.
35. Сравнение функций. Символы Ландау. Теоремы о свойствах символов.
36. Теорема о пределе частного функций. Асимптотические равенства.
37. Непрерывность функции. Свойства непрерывных функций.
38. Теоремы непрерывности обратной функции на отрезке и промежутке. Теорема о непрерывности композиции двух непрерывных функций.
39. Свойства функций непрерывных на отрезке. Теоремы Вейерштрасса (без доказательства), Больцано - Коши (без доказательства).
40. Точки разрыва и их классификация. Теоремы о точках разрыва монотонной функции.
41. Производная функции и её свойства. Теорема о непрерывности функции, имеющей производную.
42. Определение правой и левой производной. Теорема о необходимом и достаточном условии дифференцируемости функций в точке.
43.Дифференцируемость функции в точке. Теорема о необходимом и достаточном условии дифференцируемости функции в точке.
44. Дифференциал функции. Абсолютная и относительная погрешность.
45. Геометрический и физический смысл производной. Теорема о предельном положении секущей.
46. Правила вычисления производных, связанных с арифметическими действиями над функциями.
47. Производная композиции функции. Следствия.
48. Производная функции. Следствия.
49. Логарифмическое дифференцирование.
50. Дифференциал сложной функции. Инвариантная форма записи дифференциала. Производная сложной функции.
51. Производные высших порядков. Теорема о вычислении производных n - го порядка. Механический смысл второй производной.
52. Дифференциалы n -го порядка. Дифференциалы n -го порядка не обладающие инвариантной формой.
53.Параметрически заданные функции их дифференцирование. Дифференцирование неявно заданных функций.
54. Возрастание и убывание функций. Экстремум функций. Достаточный признак возрастания (убывания). Функция в точке.
55. Теоремы Ферма и Ролля. Их геометрический смысл.
56. Теорема Лагранжа о конечном приращении. Геометрический смысл.
57. Признак постоянства функции.
58. Достаточный признак локального экстремума с помощью первой производной.
59. Теорема Коши о конечном приращении.
60. Формула Тейлора. Основные разложения функций.
61. Формула Тейлора с остаточным членом в форме Лагранжа и Коши.
62. Обобщённая теорема о среднем
63.Раскрытие неопределённостей. Правило Лопиталя.
64. Исследование функций с помощью первой производной. Признак монотонности.
65. Необходимое условие существования экстремума. Достаточное условие существования экстремума по первой производной.
66. Достаточное условие существования экстремума по высшим производным.
67. Алгоритм вычисления наибольшего и наименьшего значений функции. Выпуклость и вогнутость функций. Точки перегиба.
68. Достаточное условие строгой выпуклости-вогнутости. Необходимый признак точки перегиба.
69. Асимптоты графика функции.
70.Первообразная (примитивная) функция. Теорема 1 Лемма. Теорема 2. Определение неопределённого интеграла. Геометрический смысл неопределённого интеграла. Теорема существования неопределенного интеграла.
71.Свойства неопределённого интеграла.
72. Замена переменной в неопределённом интеграле. (Теорема 1, Теорема 2).
73.Интегрирование по частям в неопределённом интеграле. Обобщённая формула интегрирования по частям. Вывод рекуррентных формул.
75.Основная теорема алгебры (теорема Гаусса). Теорема о разложении многочлена на неприводимые множители. Теорема о разложении правильной рациональной дроби на сумму элементарных дробей (б/д).
76. Способы определения неопределённых (неизвестных) коэффициентов. Практическое правило разложения правильной рациональной дроби на простые.
77. Интегрирование рациональных функций. Интеграл вида: 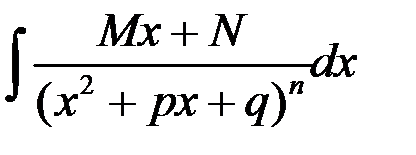
78. Интегрирование тригонометрических функций 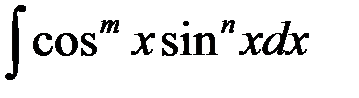 .
.
79.Интегрирование Интегрирование интегралов вида: 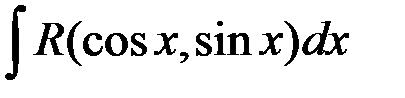 , частные случаи подстановок.
, частные случаи подстановок.
80. Интегрирование интегралов вида: 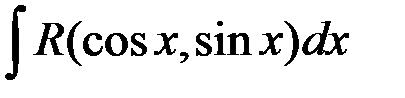 , универсальная подстановка, приведение к рациональной дроби более простыми способами.
, универсальная подстановка, приведение к рациональной дроби более простыми способами.
81. Интегрирование иррациональных функции. Интегралы вида: 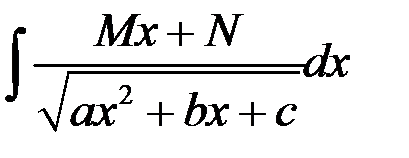 ,
, 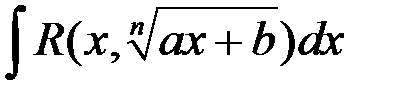
82. Интегрирование выражений, содержащих радикалы
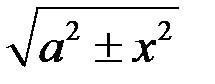 ;
; 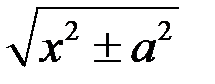 ,
, 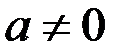
83. Интегрирование интегралов вида: 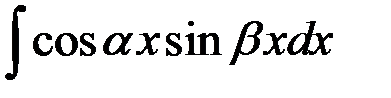 ;
; 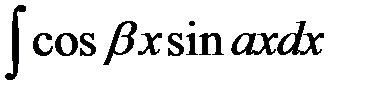
84. Интегрирование иррациональных функции вида:
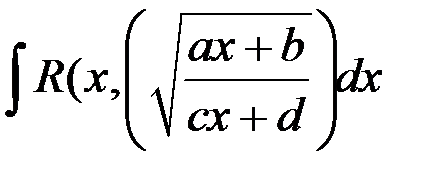 ;
; 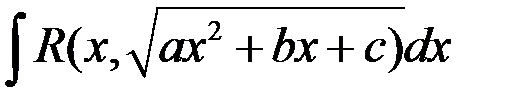
80. Интегрирование интегралов вида: 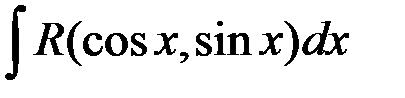 , универсальная подстановка, приведение к рациональной дроби более простыми способами.
, универсальная подстановка, приведение к рациональной дроби более простыми способами.
81. Интегрирование иррациональных функции. Интегралы вида: 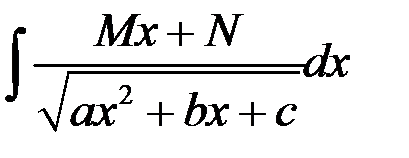 ,
, 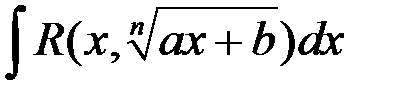
82. Интегрирование выражений, содержащих радикалы
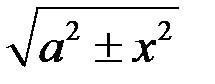 ;
; 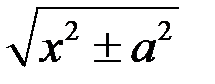 ,
, 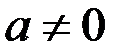
83. Интегрирование интегралов вида: 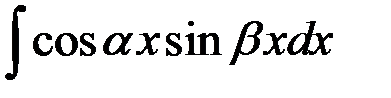 ;
; 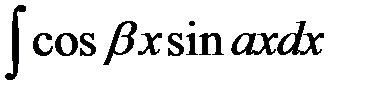
84. Интегрирование иррациональных функции вида:
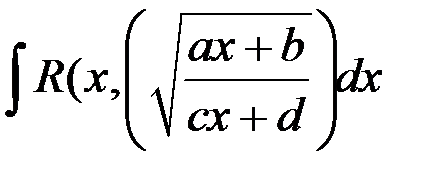 ;
; 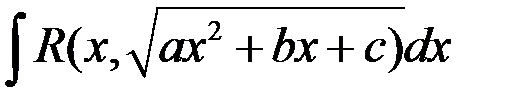
85. Вычисление интегралов вида: 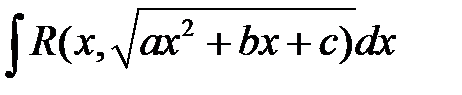 , с использованием рационализирующих подстановок Эйлера.
, с использованием рационализирующих подстановок Эйлера.
86. Метод Остроградского выделения рациональной части интеграла от рациональной дроби.
87. Метод Остроградского (неопределённых коэффициентов). Интегрирование интегралов вида: 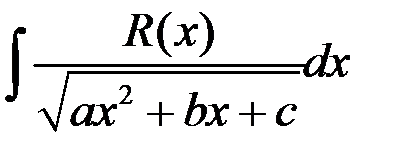
88. Интегрирование иррациональных выражений с помощью тригонометрических подстановок интегралов вида: 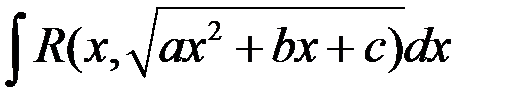 ;
; 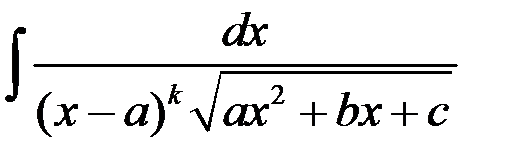
89. Интегрирование биномиальных дифференциалов: 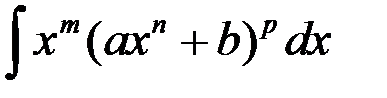
90. Интегрирование интегралов вида 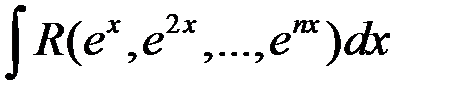
91. Определѐнный интеграл. Интегральная сумма. Задачи, приводящие к определѐнному интегралу.
92.Определение определѐнного интеграла. Геометрический смысл интегральной суммы Римана.
93. Необходимые условия существования определѐнного интеграла.
94. Теорема Дарбу - необходимое и достаточное условие существования определѐнного интеграла.
95. Свойства определѐнного интеграла.
96. Теорема о среднем в определѐнном интеграле. Следствия.
97. Определенный интеграл с переменным верхним пределом. Теоремы о
непрерывности, дифференцируемости. Следствия.
98. Основная теорема интегрального исчисления. Формула Ньютона-Лейбница.
99. Замена переменной под знаком определѐнного интеграла.
100.Интегрирование по частям в определѐнном интеграле (обобщенная теорема интегрирования по частям). Теорема интегрирования чѐтных и нечѐтных функций.
101.Понятие площади плоской фигуры. Вычисление площади плоских фигур, контур которых задан уравнениями в декартовых координатах в явном виде, в параметрическом виде, в полярной системе координат.
102. Понятие объема тела. Вычисление объема тела вращения.
103. Понятие о площади поверхности вращения. Вывод формулы для вычисления площади поверхности вращения в декартовой системе координат, в параметрической форме, в полярной системе координат.
104. Объѐм тела с известными площадями поперечных сечений. Объѐм тела вращения.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|