Тема: Действительные числа. Группа: МОЦИ-264

Тема: Действительные числа

Дата: 06.10.2020 г.

Группа: МОЦИ-264

Студенты должны знать: что такое действительное, натуральное, целое, рациональное число, периодическая дробь.

Студенты должны уметь:записывать бесконечную десятичную дробь в виде обыкновенной, выполнять действия с десятичными и обыкновенными дробями.

Актуализация знаний:

1.Какие числа называются натуральными? Привести пример.

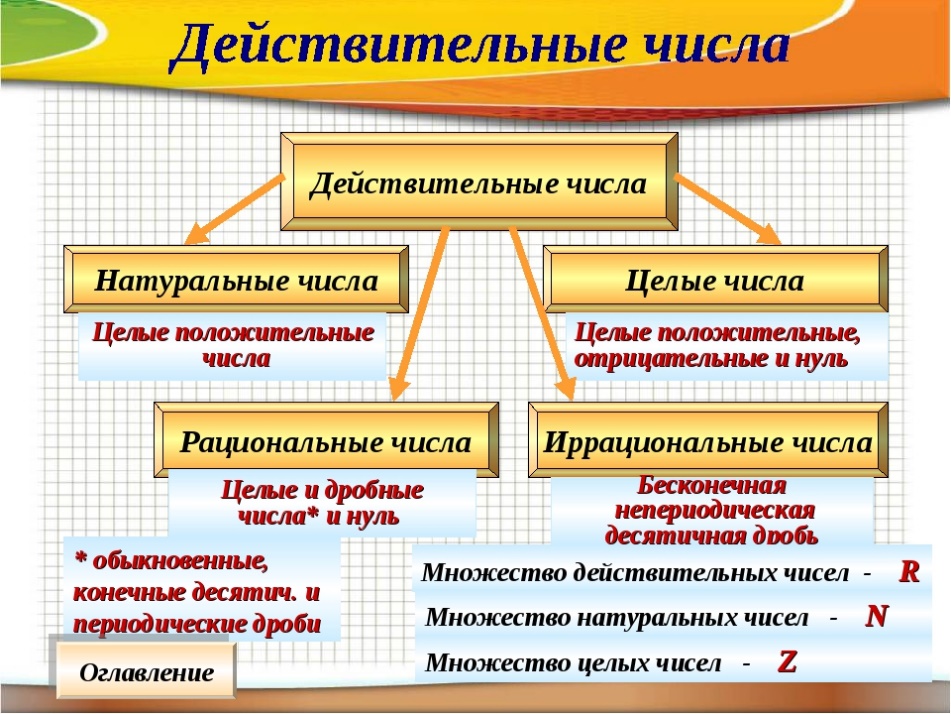
Ответ: Натуральные числа – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей.

1; 2; 3; 4;…ряд натуральных чисел

2.Является ли 0 натуральным числом?

Ответ: Нет, ноль не является натуральным числом.

3.Сколько натуральных чисел существует?

Ответ: Существует бесконечное множество натуральных чисе

4. Каково наименьшее натуральное число?

Ответ: Единица — это наименьшее натуральное число.

5. Каково наибольшее натуральное число?

Ответ: Его невозможно указать, ведь существует бесконечное множество натуральных чисел.

6. Какие числа называются целыми?

Ответ: Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.

Числа, противоположные натуральным — это целые отрицательные числа, например: -1; -2; -3; -4;…

7.Какие числа называются рациональными?

Ответ: Рациональные числа — это целые числа и дроби.

Любое рациональное число может быть представлено в виде периодической дроби. Пример:-1,(0); 3,(6); 0,(0);…

Из примера видно, что любое целое число есть периодическая дробь с периодом ноль.

Любое рациональное число может быть представлено в виде дроби m/n, где m целое число, n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера: 22/6 = 3,(6);

Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.

Ещё пример: рациональное число -9 может быть представлено в виде простой дроби как -18/2 или как -72/8.

Множество рациональных чисел обозначается латинской буквой Q.

8. Какие числа называются иррациональными?

Ответ: Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры: число пи = 3,141592 число е = 2,718281

2.Теоретическая часть

3. Самостоятельная работа:

Вариант 1

1. Представить в виде обыкновенной дроби:

а) 0,7(1); б) 1,(33); в) 0,2(18); г) 0,49(6)

2. Вычислить и записать в виде десятичной дроби:

а) 0,19(4) 9 + 13,(6) 12; б) (3+0,24) 2,15 – 0,364 :

Вариант 2

1. Представить в виде обыкновенной дроби:

а) 0,6(2); б) - 1,(5); в) 2,(88); г) - 1,3(2)

2. Вычислить и записать в виде десятичной дроби:

а) - 3,(27) 0,(04) + 0,2(7) 4,5; б) (5,1625 - 2) +0,8

Домашнее задание:

12 Следующая ⇒