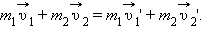ЛАБОРАТОРНАЯ РАБОТА № 4. Тема: «Изучение закона сохранения импульса». Теоретическая часть

ЛАБОРАТОРНАЯ РАБОТА № 4

Тема: «Изучение закона сохранения импульса»

Цель: проверить выполнение закона сохранения импульса при косом центральном соударении шаров.

Оборудование: штатив, два шара одинаковой массы, желоб, листы белой и копировальной бумаги, линейка, карандаш.

Теоретическая часть

Пусть на тело массой m в течение некоторого малого промежутка времени Δt действовала сила 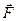. Под действием этой силы скорость тела изменилась на 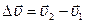Следовательно, в течение времени Δt тело двигалось с ускорением

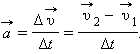
Из основного закона динамики следует:

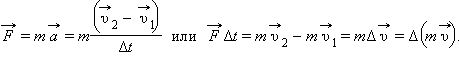
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с).

Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы также является векторной величиной.

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.

Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через 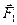и 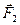. По третьему закону Ньютона 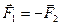. Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны: 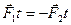. Применим к этим телам второй закон Ньютона:

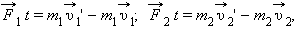
где 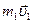и – и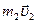мпульсы тел в начальный момент времени, 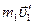и – импульсы тел в конце взаимодействия. Из этих соотношений следует:

Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.

Порядок выполнения работы:

1.Возьмите два шара одинаковой массы. Один шар установите на краю лотка таким образом, чтобы его вектор скорости при столкновении не был направлен на центр другого шара. При таком столкновении, являющемся косым центральным, векторы скоросте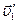й и 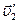шаров после столкновения имеют различные направления. По закону сохранения импульса должно выполняться равенство .

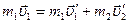Так как 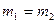, то .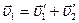

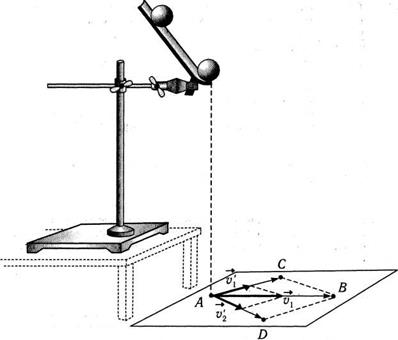2. Для проверки последнего равенства проведите серию опытов и отметьте на листе бумаги: а) точку падения шара по вертикали с края лотка (точка А); б) точку падения шара после свободного скатывания (точка В); в) точки падения шаров после их столкновения (точки С и D) (рис).

3. Соедините точку А с точками В, СиD. Вектор АВ параллелен вектору υ₁скорости первого шара до столкновения и пропорционален ему по длине. Векторы АС и AD параллельны векторам скоросте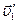й и 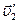шаров после их столкновения. При выполнении закона сохранения импульса сумма векторов AD и АС должна быть равна вектору АВ.

4. Постройте параллелограмм со сторонами AD и АС и проведите его диагональ из вершины А.

5. Сравните эту диагональ с вектором АВ. Сделайте вывод о сохранении импульса в данной системе.

Контрольные вопросы:

1. Что называется импульсом тела?

2. При каких условиях выполняется закон сохранения импульса?

3. Может ли неподвижное тело в результате столкновения с ним тела, движущегося со скоростью υ₁ приобрести скорость υ₂> υ₁?

4. Может ли неподвижное тело в результате столкновения с ним тела, обладающего импульсом p₁, приобрести импульс p₂> p₁?

ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Что называется импульсом тела?

2.При каких условиях выполняется закон сохранения импульса?

3.Может ли неподвижное тело в результате столкновения с ним тела, движущегося со скоростью υ₁ приобрести скорость υ₂> υ₁?

4.Может ли неподвижное тело в результате столкновения с ним тела, обладающего импульсом p₁, приобрести импульс p₂> p₁?

ОТЧЕТ ПО РАБОТЕ:

ВЫВОД: