Хелпикс

Главная

Контакты

Случайная статья



Применение определенного интеграла



Применение определенного интеграла

1. Вчисление площадей криволинейной трапеции.

План вычисления площади криволинейной трапеции:

1. Схематический чертеж.

2. Представление искомой площади как суммы или разности площадей.

3. Записать каждую функцию в виде y = f(x).

4. Вычислить площадь каждой криволинейной трапеции или площади искомой фигуры.

Площади фигур.

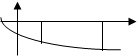
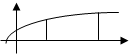 у                                                      у

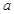
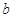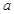
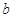            х                                          х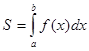                                                                          

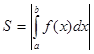
Если рассмотренная фигура не является криволинейной трапецией, тогда площадь нужно представить как сумму или разность криволинейных трапеций.     

 


                                                      m

             S1 S2                              

                                                            a           b

                S = S1 + S2                        S = S amb – S anb

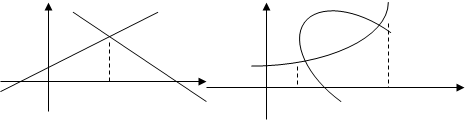
Задание №1Найти площадь фигуры, ограниченной линиями x - 2y + 4 = 0, y = 0 и x + y – 5 = 0.

Решение.Выполним построение фигуры.

Построим прямую x - 2y + 4 = 0:

Берем y = 0, x = -4, A( -4; 0); x = 0, y = 2, B(0; 2).

Построим прямую x + y – 5 = 0:

Берем y = 0, x = 5, C(5; 0); x = 0, y = 5, D(0; 5).

Найдем точку пересечения прямых, решив систему уравнений:

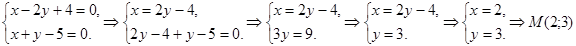
Для вычисления искомой площади разобьем треугольник AMC на два треугольника AMN и NMC, так как при изменении x от A до N площадь ограничена прямой x - 2y + 4 = 0, а при изменении x от N до С – прямой x + y – 5 = 0.

Для треугольника AMN имеем: x - 2y + 4 = 0; y = 0,5x + 2, т.е.   f(x) = 0,5x + 2, a = -4, b = 2.

 Для треугольника NMC имеем: x + y – 5 = 0, y = 5 – x, т.е. f(x) = 5 – x, a = 2, b = 5.

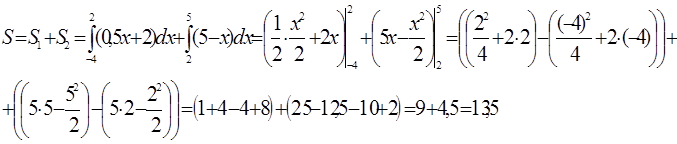
Ответ. S = 13, 5 кв. ед.

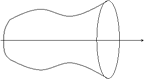
2.Вычисление объемов тел вращения.

y = f(x)  
Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.

Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса 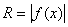, то объем тела вращения может быть легко найден по полученной выше формуле:

 

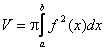
Формулы объемов тел вращения около:  

оси Ох 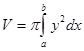;   оси Оу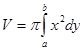

Задание №1.Вычислить объем тела, образованного вращением вокруг оси Оx площадки, ограниченной линиями y2 = 4x и y = x.

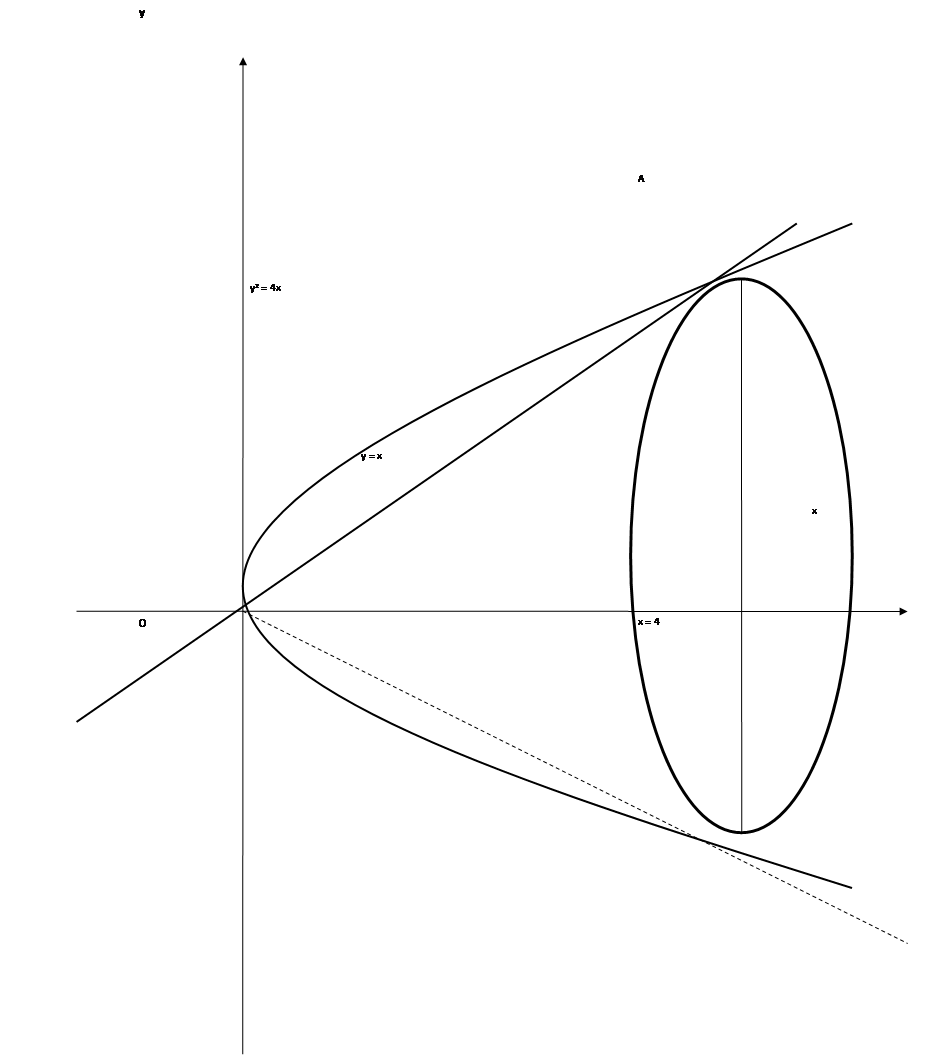Решение. Решив систему  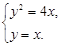находим точки пересечения параболы и прямой: О (0; 0) и А (4; 4). Следовательно, пределы интегрирования a = 0 и b = 4. Объем тела вращения представляет собой разность объемов параболоида, образованного вращением кривой y2 = 4x (V1) и конуса, образованного вращением прямой y = x (V2). Тогда

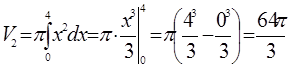
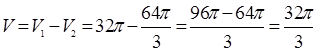
Ответ: 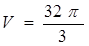 (куб. ед.)

3.Выполнить задания

Задание № 1. Найти площадь плоской фигуры, ограниченной линиями.

1) x – y + 2 = 0, y = 0, x = -1, x = 2         2) x – y + 3 = 0, x + y – 1 = 0, y = 0

Задание № 2.Найти объемы тел вращения, образованных вращением вокруг оси Оx площадей, ограниченных линиями.

1) y2 – 4x = 0, x – 2 = 0, x – 4 = 0, y = 0

2) y2 – x + 1 = 0, x – 2 = 0, y = 0

3) y = - x2 + 2x, y = 0

 

 

Справочный материал

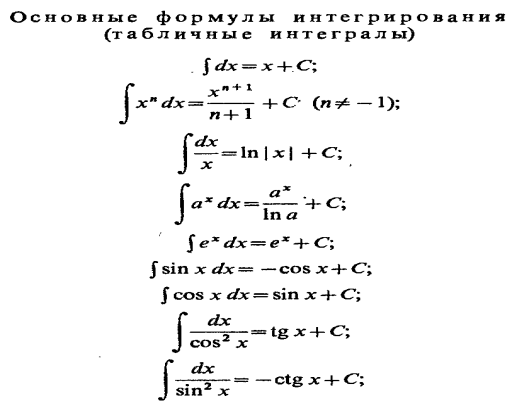
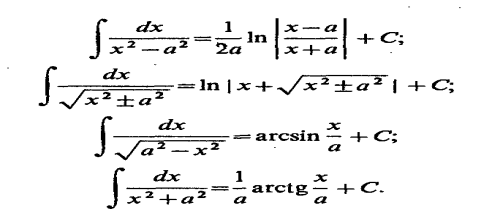
Задания посылать на электронную почту:

mila.zhelonkina.73@mail.ru
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.