
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Группа 1БУ-67. Тема: Радианный метод измерения углов вращения и связь с градусной мерой.
Группа 1БУ-67
Тема: Радианный метод измерения углов вращения и связь с градусной мерой.
Задание:
1. Изучить теоретические сведения и законспектировать их.
2. Записать примеры выполнения заданий.
3. Выполнить задания.
4. Выполненные задания сфотографировать и отправлять на электронную почту tryufelka83@mail.ru или в ЛС https://vk.com/tryufelka83 социальной сети VKontakte.
5. Выполненные задания сдать до: 02.11
Учебник: Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014.
Ссылка на учебник онлайн:
https://uchebnik-skachatj-besplatno.com/Алгебра/Учебник%20Алгебра%2010-11%20класс%20Алимов%20Колягин/index.html#prettyPhoto
с. 121-125

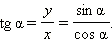
|
Котангенсом угла α называется отношение абсциссы x к ординате y точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.
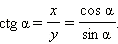
|
Вычисление тригонометрических функций некоторых углов
|
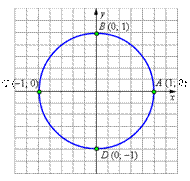
| Рисунок 2. Вычисление углов |
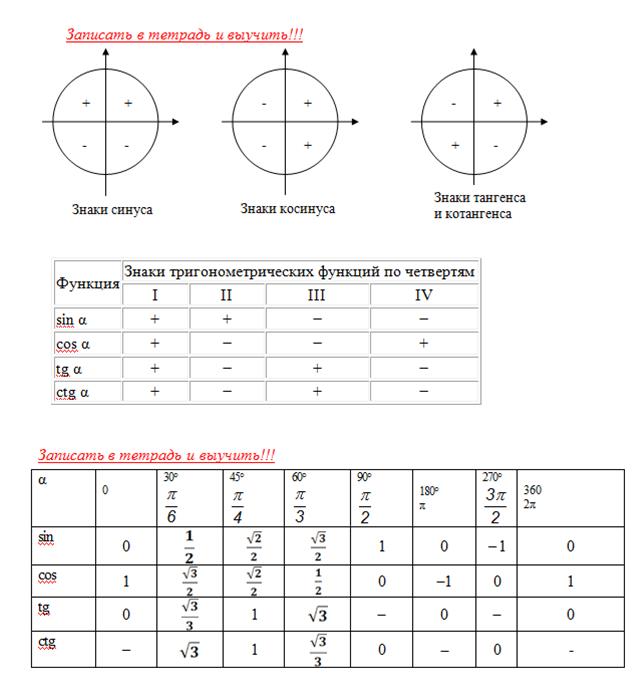
Найдём значения тригонометрических функций некоторых наиболее часто встречающихся углов. Конец радиус-вектора, отвечающего углу 0°, точка A, имеет координаты (1; 0). Поэтому cos 0° = 1, sin 0° = 0, tg 0° = 0, ctg 0° не определён. Совершенно аналогично рассматриваются точки B (0; 1), C (–1; 0) и D (0; –1), что даёт:
· sin 90° = 1,
· cos 90° = 0,
· ctg 90° = 0,
· tg 0° не определён.
· sin 180° = 0,
· cos 180° = –1,
· tg 180° = 0,
· ctg 180° не определён.
· sin 270° = –1,
· cos 270° = 0,
· ctg 270° = 0,
· tg 270° не определён.
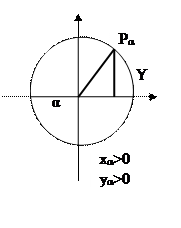 Рассмотрим единичную окружность, т.е. окружность с центром в начале координат и радиусом, равным 1. На ед. окружности отметим точку Р0 (1,0). При повороте начального радиуса около центра О на угол α радиан точка Р0 перейдет в некоторую точку Рα (xα ,yα).
Рассмотрим единичную окружность, т.е. окружность с центром в начале координат и радиусом, равным 1. На ед. окружности отметим точку Р0 (1,0). При повороте начального радиуса около центра О на угол α радиан точка Р0 перейдет в некоторую точку Рα (xα ,yα).
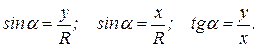
Каждому углу α соответствует единственная точка Рα (xα ,yα) и, следовательно, единственное значение синуса и косинуса этого числа. Таким образом, sin α и cos α, tgα, ctg α являются функциями числового аргумента.
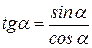
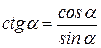
Секансом числа α, называется величина, обратная cos α, т.е. 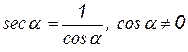

Косекансом числа α, называется величина, обратная sin α, т.е.
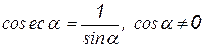
Пример
Найдите значения выражений
1) 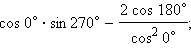 2)
2) 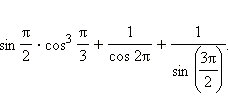
Решение
Имеем:
1) 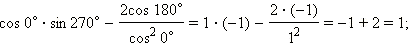 2)
2) 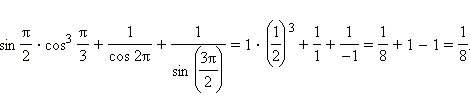 Ответ. 1) 1; 2)
Ответ. 1) 1; 2) 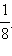
|
Домашнее задание.
1) №434 (1,2)
2) №442 (1-5)
3) Найдите числовое значение выражения:
а) 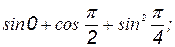
б) 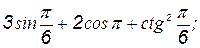
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|