
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
октября 2020 г. (среда)
21 октября 2020 г. (среда)
Дисциплина: Математика: алгебра и начала математического анализа, геометрия.
Группа: № 80
Урок № 40-41
Тема: Взаимное расположение прямых в пространстве. Угол между двумя прямыми.
Цель:
Учебная: рассмотреть взаимное расположение прямых в пространстве, понятие угла между двумя прямыми.
Развивающая: развивать математическое мышление, графические и вычислительные навыки, пространственное воображение.
Воспитательная: воспитывать у обучающихся устойчивый интерес к изучению математики; математическую культуру.
Литература: Геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / Л.С. Атанасян, В.Ф. Бутузов [и др.] – М.: Просвещение, 2013.
Материалы урока: !!! РИСУЕМ ПРАВИЛЬНО, НЕ МЕНЕЕ 5 СМ!
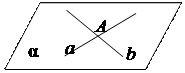
| Прямые в пространстве могут пересекаться и при этом образовывать четыре угла. Прямые, которые имеют одну общую точку называются пересекающимися. a Ç b = A, a Ì a, b Ì a
| |
| Один из четырёх углов (b), который не превосходит любого из трёх остальных углов, называют углом межде пересекающимися прямыми. 0o < b £ 90o | ||
|
a || b | Параллельными называются две прямые, которые принадлежат одной плоскости и не имеют общей точки (а ∩ b = Ø – прямые а и b непересекаются; а Ì a; b Ì a). Угол между параллельными прямыми равен 0о. | |
|
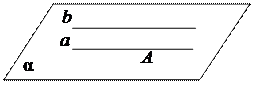
| Через две параллельные прямые можно провести плоскость и только одну. Пусть прямые а и b параллельны. Через параллельные прямые а и b можно провести плоскость. Эта плоскость единственная, потому что если взять на прямой а точку А, то через точку А и прямую b можно провести только одну плоскость. | |
|
| Возьмём прямую а и вне её точку А. Через них можно провести единственную плоскость a, а в этой плоскости через точку А можно провести единственную прямую b || а, т.е. в пространстве через точку, расположенную вне прямой можно провести только одну прямую, параллельную данной. | |
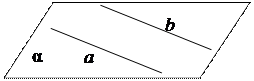
| В пространстве существуют прямые, через которые нельзя провести плоскость. Пусть прямая а принадлежит плоскости a (а Ì a), прямая b пересекает плоскость a в точке В (b ∩ a = В). Допустим, что через прямые а и b можно провести плоскость b, тогда точка В прямой b тоже будет принадлежать плоскости b. Значит, плоскость a и b будут иметь общие прямую а и вне её точку В и потому плоскости a и b совпадут. Отсюда следует, что прямая b тоже принадлежит плоскости a, а это противоречит условию b Ç a. Остаётся сделать заключение, что через прямые а и b нельзя провести плоскость. | ||

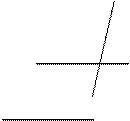
| Две прямые, которые не лежат в одной плоскости и не пересекаются, называются скрещивающимися.
Скрещивающиеся прямые в кабинете моделируют, например, края пола у передней стены и потолка у боковой стены. | |
 b
с В
а b
с В
а
|
Пусть а || с, с ∩ b = В, тогда угол между скрещивающимися прямыми а и b равен углу между пересекающимися прямыми b и с. | |
Решить задачи:
1. Точка М не лежит в плоскости треугольника АВС. Каково взаимное расположение прямых МА и ВС?
Решение.
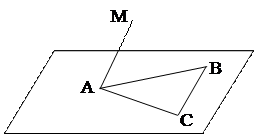
| Точка МÏ (АВС). Выясним, как расположены прямые МА и ВС. Прямые МА и ВС не лежат в одной плоскости, иначе они были бы либо параллельны, либо пересекались. В обоих случаях точка М лежала бы в плоскости, проходящей через точки А, В и С, что противоречит |
условию. Но прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.
Ответ:скрещиваются.
2. Точки А,В,С и D не лежат в одной плоскости. Каково взаимное расположение прямых АВ и СD?
Решение.
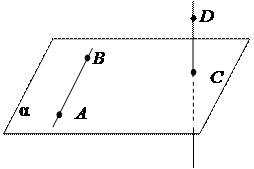
| Пусть точки А, В, С и D не лежат в одной плоскости. Определим взаимное расположение прямых АВ и СD. Никакие из трёх данных точек не лежат на одной прямой, т.к. иначе через эти четыре точки можно провести плоскость, что противоречит условию. Пусть a – плоскость, в которой лежат точки А, В, С и не лежит точка D. Тогда, если прямая АВ Ì a, а прямая |
СD ∩ a = С, С Ï АВ, то АВ 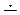 СD.
СD.
Ответ:скрещивающиеся.
Домашнее задание:ответить на вопрос № 10 стр.31.
ФОТОГРАФИРУЕМ И ОТСЫЛАЕМ ЕЛЕНЕ АНАТОЛЬЕВНЕ
ВСЕ ВЫПОЛНЕННЫЕ ДОМАШНИЕ ЗАДАНИЯ И КОНТРОЛЬНЫЕ РАБОТЫ!!!!!!!!
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
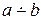 .
.