Контакты

Случайная статья

Занятие №19 Группа 1 АБ Дата проведении: 20.10.20г.

Стр 1 из 2Следующая ⇒

Занятие №19 Группа 1 АБ Дата проведении: 20.10.20г.

Тема. Корни натуральной степени из числа и их свойства

Просмотреть видеоурок по ссылке: https://yandex.fr/video/preview?text=видео%20арифметический%20корень%20натуральной%20степени%2010%20класс&path=wizard&parent-reqid=1603102291246714-170218469085970899500113-production-app-host-man-web-yp-51&wiz_type=vital&filmId=11157328589993913273

1. Перечень вопросов, рассматриваемых на занятии:

· преобразование и вычисление арифметических корней,

· свойства арифметического корня натуральной степени,

· корень нечетной степени из отрицательного числа,

· какими свойствами обладает арифметический корень натуральной степени.

2. Глоссарий

Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.
Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.
Арифметическим корнем натуральной степени, где n ≥ 2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.

3. Объяснение темы «Арифметический корень натуральной степени»

Решим задачу.

Площадь квадрата S=16 м².

Обозначим сторону квадрата а, м.

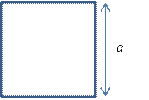
Тогда, а² = 16.

Решим данное уравнение:

a=4и а= –4.

Проверим решение:

4² = 16;

(–4)² = 16.

Ответ: длина стороны квадрата равна 4 м.

Определение:

Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.

Определение:

Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.

Обозначение: .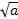

Определение:

Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.

Обозначение: .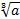

Например:

.

.

.

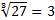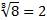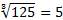На основании определений квадратного и кубического корней, можно сформулировать определения корня n-ой степени и арифметического корня n-ой степени.

Определение:

Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.

Определение:

Арифметическим корнем натуральной степени, где n≥2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.

Обозначение: 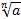– корень n-й степени, где

n–степень арифметического корня;

а– подкоренное выражение.

Давайте рассмотрим такой пример: .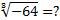

Мы знаем, что (–4)³ = –64, следовательно, .

Еще один пример: .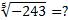

Мы знаем, что (–3)⁵ = –243, следовательно, .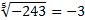

На основании этих примеров, можно сделать вывод:

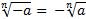, при условии, что n –нечетное число.

Свойства арифметического корня натуральной степени:

Если а ≥ 0, b ≥ 0 и n, m – натуральные числа, причем n ≥ 2, m ≥ 2, то справедливо следующее:

.

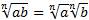Примеры:

.

.

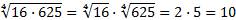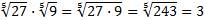2. .

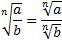Примеры:

.

.

.

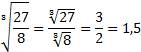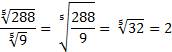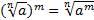Пример:

.

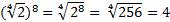3. .

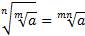Пример:

.

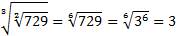4. Для любого а справедливо равенство:

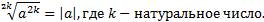
Пример:

Найдите значение выражения 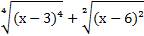, при 3 <x< 6.

Степени заданных арифметических корней 4 и 2, четные числа, следовательно, мы можем применить свойство №5:

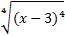=|x – 3| = х – 3, т.к. х>3;

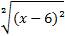=|x – 6|=6 – x, т.к. х<6.

Получаем: х – 3 + 6 – х= 3.

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.