Текст к презентации “Опыты Кавендиша по определению плотности Земли”

Текст к презентации “Опыты Кавендиша по определению плотности Земли”

Слайд	Текст

В 1797-98 г. английский физик Генри Кавендиш поставил серию опытов, позволивших измерить силу тяготения в лабораторных условиях и определить среднюю плотность Земли.

В XVII - XVIII веках учёными разных стран проводятся серьёзные исследования Земли как планеты.

● Изучается Земля как планета Солнечной системы, в том числе, в рамках формулирования Ньютоном закона Всемирного тяготения.

● Исследуется форма Земли и её геометрические размеры, в том числе определяется длина дуги 1⁰ меридиана, (для этого организуются экспедиции).

● Определяются значения ускорения свободного падения (для этого измеряется длина секундного маятника).

● Выдвигаются гипотезы о происхождении и строении Земли.

По последнему пункту существуют различные точки зрения. Так, И. Ньютон замечает в своих “Математических началах натуральной философии”, что плотность Земли – больше плотности воды. Из этого следует, что Земля не может быть полой внутри. В тоже время астроном Эдмонд Галлей в 1692 г. полагал, что Земля состоит из оболочки, двух внутренних концентрических оболочек и центрального ядра с диаметрами, соответствующими Венере, Марсу и Меркурию. Оболочки разделены атмосферами, и у каждой оболочки есть свои магнитные полюса, внешние оболочки вращаются быстрее внутренних.

Перед Наукой стоит задача формирования представлений о строении Земли, её размерах и плотности, кроме того определение плотности Земли, а значит и её массы, позволит вычислить массы других астрономических тел, и это также одна их задач Науки той эпохи.

В XIX веке о геологическом строении Земли, её геометрии существуют и углубляются довольно верные представления, плотность Земли более не вызывает сомнения, и сравнивается с плотностями известных горных пород, как это следует из слов великого физика Ф. Араго. Но то, как этого достигла Наука, всё ещё представляется удивительным. Попробуем проследовать этим путём.

Исследуя форму Земли и проводя измерения длины 1⁰ меридиана в экспедиции в Перу в 1737-40 гг. П. Бугер, установил, что отвес отклоняется на 8′′ от вертикали вблизи потухшего вулкана Чимборасо, эти первые измерения были неточны, но экспериментально было показано, что плотность Земли много больше 1 г/см³. Позже шотландский физик Маскелайн выбрал “идеальную гору” конической формы – холм Шихэлиен, и точнее определил плотность Земли, измерив α – угол отклонения отвеса из-за притяжения к горе.

Лабораторный способ измерения сил гравитационного взаимодействия, а значит и определения плотности Земли был предложен английским священником и естествоиспытателем (учёным) Джоном Мичеллом. Он предложил определять силы взаимодействия тел по углу закручивания коромысла крутильных весов, идея была им высказана Г. Кавендишу ранее того, как Ш. Кулон опубликовал свои результаты по взаимодействию электрически заряженных тел, полученные с помощью аналогичных весов. Мичелл создал первую экспериментальную установку, но не успел осуществить задуманного. Разработкой опытов и усовершенствованием конструкции прибора занялся лорд Г. Кавендиш.

На первом плане у Кавендиша выступает, как он пишет сам, идея крутильных весов, предложенная Митчеллом, однако его статья позволяет более точно сформулировать идею эксперимента.

Идея эксперимента состояла в том, чтобы определить плотность Земли через отношение силы, с которой тело (свинцовый шар) притягивается к Земле, к силе, с которой оно притягиваются к другому телу известной массы (тяжёлый свинцовый шар), последнюю определить экспериментально с помощью крутильных весов, к коромыслам которых прикреплены меньшие шары.

Сравним силу взаимодействия небольшого свинцового шара с Землёй и с тяжёлым шаром. Отношение этих сил будет определяться геометрией тел (как раз к этому времени средний радиус Земли учёные определили довольно точно), плотностями Земли (её то и нужно определить!) и свинца, а также расстояниями сближения шаров из-за притяжения

Внимательное прочтение работы Кавендиша позволяет сформулировать некоторую модель, в рамках которой можно проанализировать опыты, поставленные Кавендишем.

В явном виде у самого Кавендиша такой модели нет.

Чувствительность весов такова, что они будут испытывать крутильные колебания.

Положения модели:

1. Колебания коромысел весов являются незатухающими.

2. Деформация кручения подвеса упругая и подчиняется закону Гука.

3. Подвес и коромысло невесомы.

4. Гравитационное взаимодействие между частями установки кроме шаров отсутствует.

5.Сила притяжения прямо пропорционально произведению масс тел и обратно пропорциональна квадрату расстояния между ними (закон всемирного тяготения).

Запишем выражение для силы, с которой Земля притягивает свинцовый шар m, прикреплённый к коромыслу весов. Считая Землю шаром выразим её массу через плотность и объём сферы известного радиуса.

Аналогично рассмотрим взаимодействие данного шара с тяжёлым свинцовым шаром массой M. Найдём отношение сил, с которыми данный шар взаимодействует с Землей и тяжёлым шаром. Вот эту силу F_ш необходимо было измерить в эксперименте.

Мы задействовали два последних положения модели.

Обратимся к тому, как экспериментально измерить силу притяжения с помощью крутильных весов. Притягиваясь, шары m и M закручивают нить подвеса на угол φ = nδ (число делений на цену деления) относительно положения покоя весов.

На коромысло действует пара сил, создающих относительно точки подвеса коромысла вращающий момент, плечо каждой силы l.

При упругой деформации, вызываемой парой сил, также справедлив закон Гука, но записывается он несколько по-иному.

Чувствительные весы совершают колебания, период колебаний определяется массой грузов, длиной коромысла и коэффициентом жёсткости подвеса, который входит в закон Гука. Во времена Кавендиша периодом колебаний называли полупериод одного полного колебания.

Мы задействовали три первых положения модели.

Зная полупериод колебаний, то, на сколько сместилось положение равновесия колеблющегося коромысла за счёт притяжения тяжёлого свинцового шара и шара на коромысле, расстояние взаимодействия шаров, получаем выражение для средней плотности Земли через величины, измеряемые в эксперименте.

При заданном начальном положении шаров, к примеру, Кавендиш их размещал на расстоянии 8,85 дюйма или ок. 22,5 см, измеренном смещении и известном полупериоде колебаний, достаточно знать из опыта две последние величины: смещение и полупериод, чтобы рассчитать среднюю плотность Земли.

У Кавендиша нет в работе подобной формулы, он пользовался другими математическими приёмами, например, вместо ускорения свободного падения использовал длину нитяного маятника, полупериод колебаний которого 1 с. Тем не менее, современными методами, исходя из положений модели, которые неявно заложены в работе Кавендиша, мы пришли к верному пониманию, что и как нужно измерять в подобном эксперименте.

10.

Рассмотрим подлинный чертёж установки Г. Кавендиша из его статьи. Вся она помещалась в деревянный кожух из красного дерева. Установка представляла собой деревянное сосновое коромысло с прикреплёнными к его концам небольшими свинцовыми шарами диаметром около 5 см. Коромысло подвешено на нити из посеребрённой меди длиной ок. 1 м. К этим шарам с помощью специальной поворотной фермы, ось вращения которой совпадает насколько возможно точно с осью нити, подводились два свинцовых шара существенно бо́льшего диаметра жёстко закреплённые на ферме массой по 158 кг, каждый. Вследствие гравитационного взаимодействия малых шаров с большими коромысло отклонялось на некоторый угол. Описывая установку, Кавендиш указывает, что минимальное деление, которое указывало угол поворота 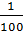дюйма или 0,25 мм. Чтобы увидеть такое незначительное смещение использовались зрительные трубы и подсветка от ламп с собирающими линзами.

11.

Подготовка к экспериментам шла довольно долго. Кавендиш получил установку Мичелла не ранее1793 г., а опыты, обустроенные в отдельно стоящем здании его усадьбы на окраине Лондона, начались лишь летом 1797 г. и продолжались почти год до конца мая 1798 г., при этом ставились разные серии экспериментов, установка Мичелла подверглась существенной переделке.

Некоторые параметры установки приведены на слайде, они дают представления о реальных масштабах опытов. Ещё раз обратите внимание, что вместо ускорения свободного падения Кавендиш использовал длину секундного маятника, сегодня мы легко по ней можем вычислить то значение, g, которое по сути вошло в расчёты Кавендиша.

Период колебаний коромысла в опытах был разным, поскольку Кавендиш в ходе экспериментов изменял проволоку подвеса с более мягкой на более жёсткую.

12.

Рассмотрим те экспериментальные “трудности”, с которыми столкнулся Кавендиш и их решения.

● Установка помещалась в отдельном здании; массивные столбы, на которых она была смонтирована, были вкопаны в землю - всё это было сделано, чтобы не допустить колебания прибора как целого. Перемещение двух грузов почти по 160 кг также требовало прочной конструкции.

● При измерении смещения коромысла учитывался затухающий характер колебаний.

● Использование двух зрительных труб позволяло контролировать проведение эксперимента в двух диаметрально противоположных точках: если бы снимаемые показания заметно отличались, то это могло говорить о каких-то неполадках в проводимом опыте.

● Прибор помещался в кожухе из красного дерева, в дополнительном кожухе находились маленькие шары, это исключало влияние потоков воздуха.

● Была сделана специальная защита, чтобы при колебаниях малые шары на коромысле не ударялись о корпус.

● В специальных сериях опытов инструментально, т.е. с помощью термометров, измерялась разность температур тяжёлых шаров (термометр вставлялся в отверстие, высверленное в шаре) и окружающих частей установки.

Разность температур могла породить конвекционные токи воздуха. Кавендиш оценил эффект показав, что он минимален. Чтобы минимизировать нагрев от ламп, они освещали лишь небольшую часть шкалы.

● Предположив, что на закручивание подвеса может оказать влияние магнитное взаимодействие железных стержней фермы и свинцовых шаров, Кавендиш заменил стержни медными, получив, практически те же результаты. В специальных опытах он подвергал шары действию сильных 25-см магнитов, однако, эффект магнитного действия шаров обнаружен не был.

● Предположив, что на упругость проволоки может влиять остаточная деформация, Кавендиш ставил специальные опыты.

Преодоление “трудностей” в специальных сериях экспериментов – это, с другой стороны, обоснование того, что наблюдаемый эффект поворота коромысла может быть объяснён только гравитационным притяжением шаров. Отметим, что Кавендиш проверял выполнение законы Гука, а также учитывал те изменения, которые вносит затухающий характер колебаний коромысла.

13.

На слайде показано, как Кавендиш обрабатывал результаты предварительных опытов:

● Крайние точки, отмеченные в делениях шкалы, показывают, что колебания носят затухающий характер. Как определить ту точку, в которой остановилось бы коромысло, будучи выведенным из состояния покоя? Кавендиш предлагает свой способ расчёта.

“Предположим, что коромысло покоится и его положение определено. Пусть затем грузы сдвигаются. Вследствие этого коромысло не только сдвинется, но будет вынуждено колебаться и его колебания будут продолжаться довольно долго. Поэтому, чтобы выяснить, насколько сдвинуто коромысло, необходимо найти крайние точки колебания и отсюда определить точку, в которой оно оказалось бы в покое, если бы его движение было уничтожено, или точку покоя, как я буду ее впредь называть. Для этого я наблюдал три последовательные крайние точки колебания и брал среднее между первой и третьей точками, а затем принимал среднее между ней и второй крайней точкой за точку покоя. Так как колебания непрерывно уменьшались, очевидно, что среднее между двумя крайними точками не могло дать истинную точку покоя. Можно подумать, что более точно было бы наблюдать много крайних точек колебания, чтобы находить точку покоя по разным сериям из трех крайних отклонений и брать средний результат. Однако надо отметить, что, несмотря на предосторожности, соблюдавшиеся во избежание какой-либо возмущающей силы, коромысло редко будет оставаться в покое в течение целого часа. По этой причине лучше определять точку покоя из наблюдений, выполненных, насколько это возможно, сразу же после передвижения грузов

Вторая величина, которую надо определить, - это время колебания. Ее я нахожу следующим образом: определяю две крайние точки колебания, а также моменты времени, в которые коромысло достигает двух данных делений между этими крайними точками, …. Затем я рассчитываю среднюю точку колебания и с помощью пропорции нахожу момент времени, в который коромысло проходит через среднюю точку”.

Мы познакомились с фрагментом из оригинальной работы Кавендиша, которая иллюстрирует процедуру измерения. Полупериод колебаний в этом опыте составил 7 минут.

14.

В эксперименте тяжёлые шары располагались то в “положительном” положении ww, то в “отрицательном” WW, как показано на рисунке.

В таблице окончательных результатов мы видим, что Кавендиш измерял среднее время колебаний и смещение шаров при движении из среднего положения в положительное, среднего в отрицательное и т.п.

Он также оценивал, проводя специальные расчёты, влияние того факта, что в действительности коромысло и другие части установки были не невесомы – обладали массой.

Для каждого из опытов учёный определял плотность Земли. Среднее значение по 23 основным опытам, как их определил сам Г. Кавендиш, проведённым с 12 августа 1797 по 30 мая 1798 г. составило 5,48 г/см³.

“By a mean of the experiments made with the wire first used, the density of the earth comes out 5,48 times greater than that of water; and by a mean of those made with the latter wire, it comes out the same;… the extreme results do not differ from the mean by more than 0,38, or 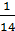of the whole.”

Мы начали изложение опытов с формулирования положений модели, которых в явном виде у Кавендиша не было, однако, и экспериментально и расчётами он проверял эти положения, границы их применимости, учитывал то, насколько отклонение от них влияет на конечный результат.

15.

Кавендиш своими экспериментами, по сути, ответил на те задачи науки, которые стояли ещё со времён Ньютона. Отметим при этом, что ему удалось довольно точно измерить силы гравитационного взаимодействия между обычными “земными” телами, а также то, что он определил своими опытами путь экспериментального исследования той задачи, которая ещё не стояла перед наукой его времени – гравитационной постоянной.

16.

Впервые гравитационная постоянная была введена Пуассоном в сочинении, вышедшем через год после смерти Кавендиша. Её не было ни в трудах Ньютона, ни Кавендиша. Пуассон указал физический смысл этой постоянной, как силы притяжения на единичном расстоянии единичных масс, её фундаментальную природу, как характеристики гравитационный свойств и её постоянный характер.

“…пусть единица силы будет, как и в № 198, постоянно ускоряющая сила, которая производит в единицу времени скорость, равную единице длины. Представим теперь себе два тела, массы которых соответственно равны массе принятой за единицу, и пусть они удалены друг от друга на величину, равную единице длины, то, если f обозначает силу притяжения одного из этих двух тел к другому, то есть, численное отношение интенсивности силы притяжения к той силе, которая была принята за единицу, а M и m были бы массы Солнца и планеты, то движущей силой планеты на расстоянии единицы длины будет Mmf, а на любом другом расстоянии r, то это будет 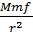. Величина, которую мы обозначим через f, зависит от притягательной силы, которой наделена материя; когда массы и расстояния равны, эта сила одинакова для всех тел; до сих пор не наблюдалось ничего, что приводило бы нас к предположению, что она увеличивается или уменьшается со временем; и у нас есть все основания полагать, что она была и будет оставаться постоянно той же самой”.

17.

Кавендиш реализовал способ измерений (идею свою и Мичелла), которые продолжались весь XIX век, плотность Земли определялась всё точнее и точнее… но только примерно через 80 лет и другим способом, используя метод обычных весов, была определена гравитационная постоянная.

18.

Значение фундаментальной константы – гравитационной постоянной, а не плотность Земли, стало целью исследований экспериментаторов ХХ века, при этом использовалась идея крутильных, торсионных, весов. Это отвечало новым задачам Науки, и всё чаще имя лорда Генри Кавендиша вспоминают в связи с определением этой константы.

Но Кавендиш “взвесил” Землю, это было важно, нужно, интересно для Науки XVIII и XIX веков.

Будем надеяться, что это интересно и тем, кто посмотрел презентацию.