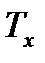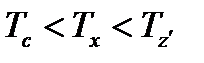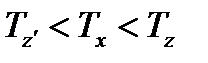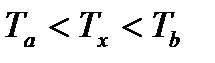- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
РАСЧЁТ ЦИКЛОВ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ ВНУТРЕННЕГО СГОРАНИЯ»
МИНИСТЕРСВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ
ФГБОУ ВПО “Великолукская государственная сельскохозяйственная академия”
Инженерный факультет
Кафедра “Автомобили, тракторы и сельскохозяйственные машины”
КОНТРОЛЬНАЯ РАБОТА
по дисциплине “Теплотехника”
«РАСЧЁТ ЦИКЛОВ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ ВНУТРЕННЕГО СГОРАНИЯ»
Выполнил: студент ЭЛ 31 группы
Двойнев Д.Н
Принял: преподаватель
Максимов Н.М.
Великие Луки
Исходные данные для расчёта
Рабочее тело обладает свойствами:
а) газовая смесь по массе - 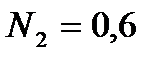 ;
; 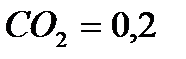 ;
; 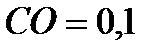 ;
; 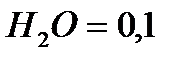
б) давление в начале сжатия - 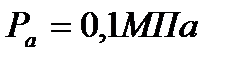
в) температура в начале сжатия - 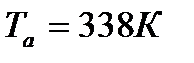
г) степень сжатия двигателя - 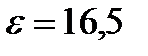
д) степень повышения давления - 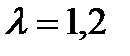
е) степень предварительного расширения - 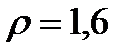
ж) количество подведённой теплоты - 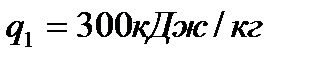
1. Изображение цикла в P-ν и T-s-диаграммах и указание термодинамических процессов, из которых он состоит.
Так как из исходных данных известно, что степень предварительного расширения ρ=1,6 и степень повышения давления λ=1,2, то это свидетельствует о том, что рассматриваемый мною цикл – это цикл Тринклера (цикл со смешанным подводом теплоты).
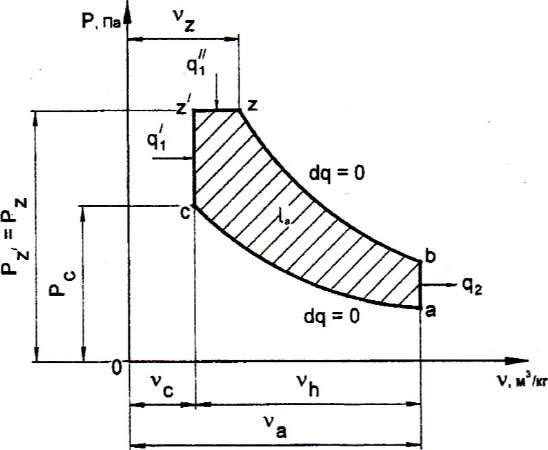
Рисунок 1 - Диаграмма цикла двигателя внутреннего сгорания со смешанным подводом теплоты, при ν=const и P=const в P-ν- координатах
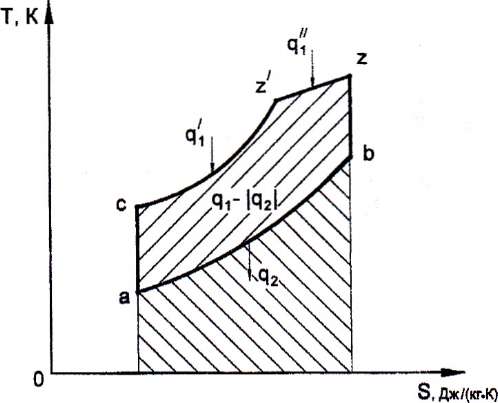
Рисунок 2 - Диаграмма цикла двигателя внутреннего сгорания со смешанным подводом теплоты, при ν=const и P=const в T-s- координатах
Цикл двигателя внутреннего сгорания со смешанным подводом теплоты состоит из следующих термодинамических процессов:
ac – адиабатное сжатие рабочего тела;
cz’ – изохорный подвод теплоты при ν=const (в реальном двигателе сжигание топлива);
z’z – изобарный подвод теплоты при p=const (в реальном двигателе досжигание топлива);
zb – адиабатное расширение рабочего тела;
ba – изохорный отвод теплоты в охладитель.
2. Определение параметров рабочего тела в характерных точках цикла.
Для определения параметров рабочего тела, определю сначала:
- газовую постоянную для смеси R, Дж/(кг  К);
К);
- коэффициент Пуассона, показатель адиабаты смеси K.
Газовую постоянную смеси можно найти из формулы
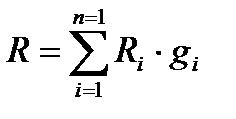 (1)
(1)
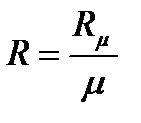 , (2)
, (2)
где 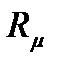 - универсальная газовая постоянная (
- универсальная газовая постоянная ( 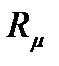 =8314 Дж/(кмоль
=8314 Дж/(кмоль  К));
К));
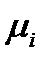 - молярная масса смеси и компонента, кг/кмоль (таблица А.1 (Приложение А));
- молярная масса смеси и компонента, кг/кмоль (таблица А.1 (Приложение А));
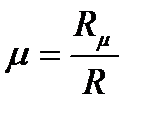 (3)
(3)
Подставляя известные значения величины в формулу (1), получаю
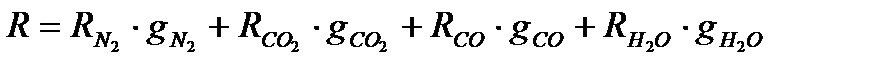 (4)
(4)
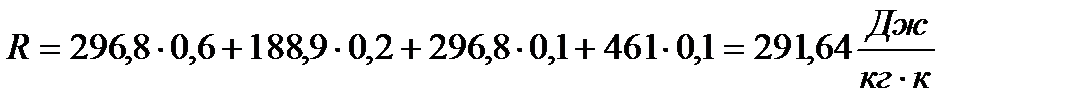
Теперь найду молярную массу, подставив данные в выражение (3)

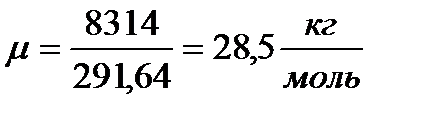
Определение показателя адиабаты K
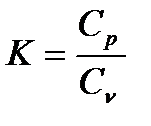 , (5)
, (5)
где 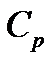 и
и 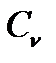 - массовые теплоёмкости смеси кДж/(кг
- массовые теплоёмкости смеси кДж/(кг  К)
К)
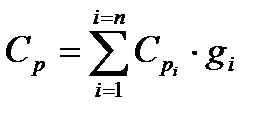 , (6)
, (6)
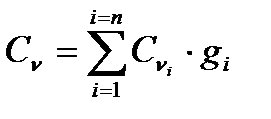 , (7)
, (7)
где 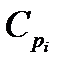 и
и 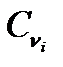 - массовые теплоёмкости компонентов смеси, Дж/(кг
- массовые теплоёмкости компонентов смеси, Дж/(кг  К)
К)
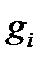 - массовая доля компонентов в смеси.
- массовая доля компонентов в смеси.
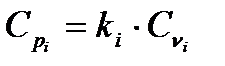 , (8)
, (8)
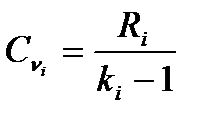 , (9)
, (9)
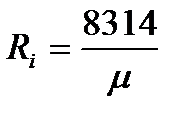 , (10)
, (10)
где 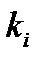 - показатель адиабаты компонента (таблица А.1 (Приложение А));
- показатель адиабаты компонента (таблица А.1 (Приложение А));
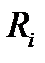 - газовая постоянная компонента, кДж/(кг
- газовая постоянная компонента, кДж/(кг  К).
К).
Из таблицы А.1 (Приложение А) нахожу показатель – К для каждого компонента смеси: K 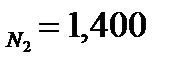 ; K
; K 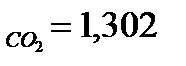 ; K
; K 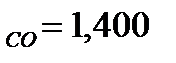 ; K
; K 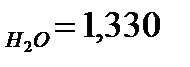
Подставляя известные величины в формулы (9) и (10), получаю
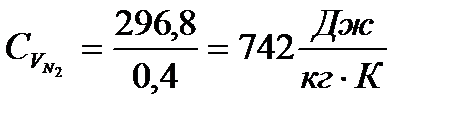
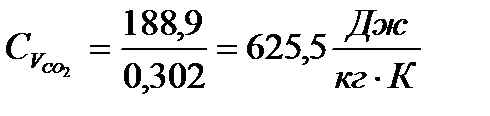
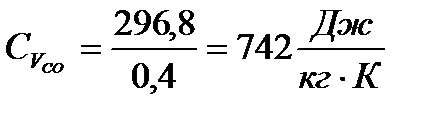
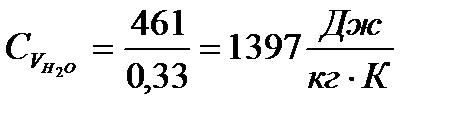
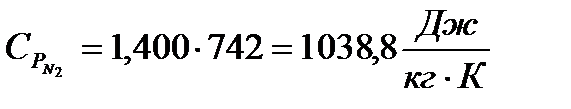
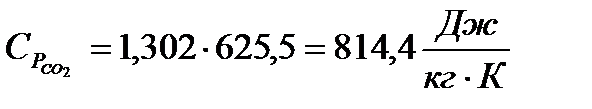
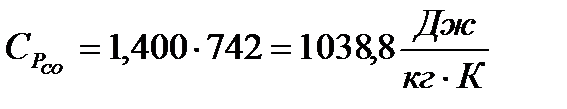
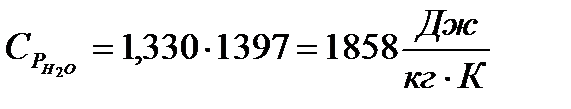
Теперь нахожу  и
и 
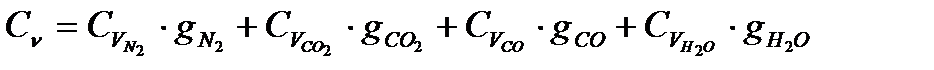 (11)
(11)
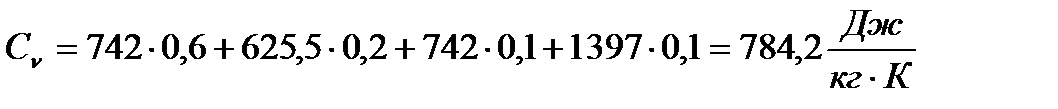
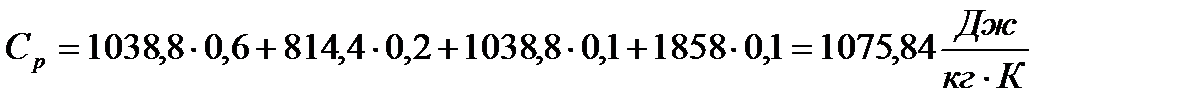
Зная  и
и 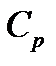 , найду К
, найду К
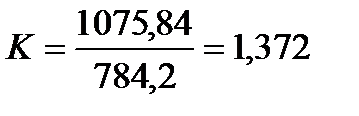
Определяю параметры в характерных точках цикла (рисунок 1).
Параметры точки «а»:
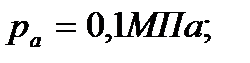
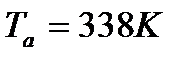
Удельный объём точки «а», найду из формулы
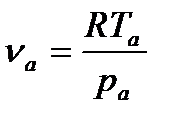 (13)
(13)
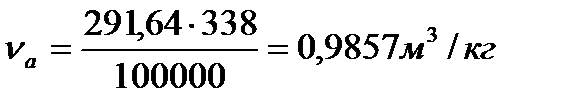
Параметры точки «с»:
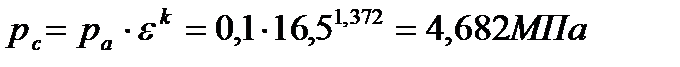 (14)
(14)
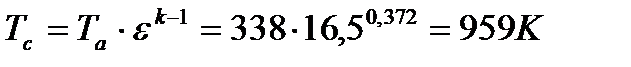 (15)
(15)
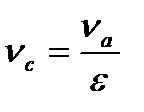 (16)
(16)
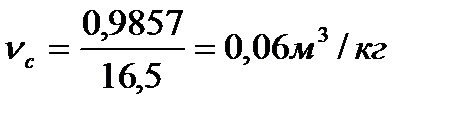
Параметры точки «z’»:
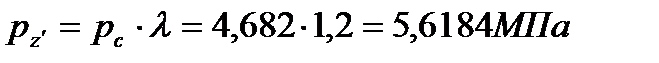 (17)
(17)
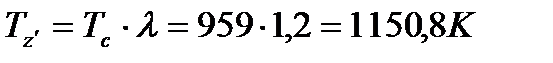 (18)
(18)
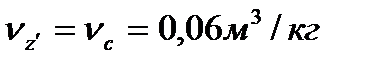
Параметры точки «z»:
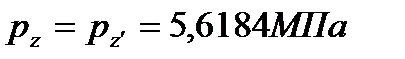
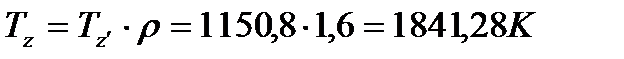 (19)
(19)
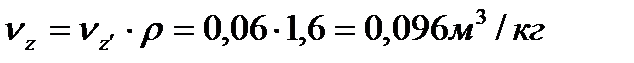 (20)
(20)
Параметры точки «b»:
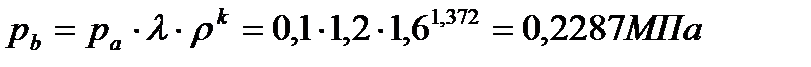 (21)
(21)
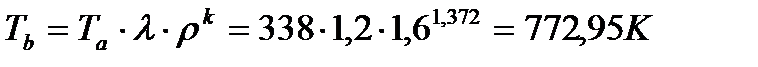 (22)
(22)
3. Определение термического КПД двигателя через параметры цикла.
Термический КПД для цикла со смешанным подводом теплоты определяется по формуле
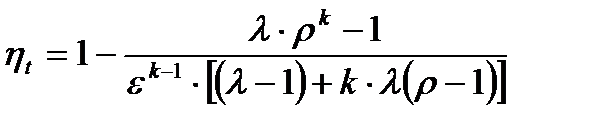 (23)
(23)
Подставляя известные значения в формулу (23), получаю
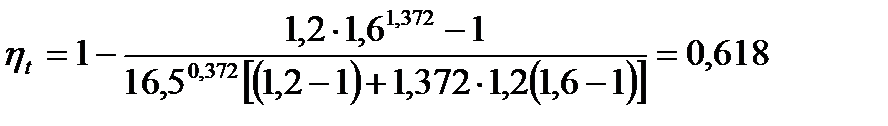
или 
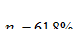
4. Определение количества подведённой и отведённой теплоты.
Определяю количество подведённой теплоты, кДж/кг, по формуле
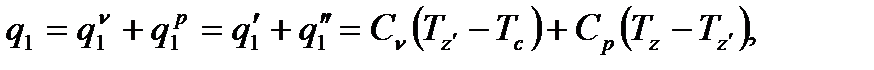 (24)
(24)
где 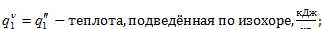
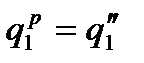 - теплота, подведённая по изобаре, кДж/кг.
- теплота, подведённая по изобаре, кДж/кг.
Подставляя известные величины в формулу (24), получаю
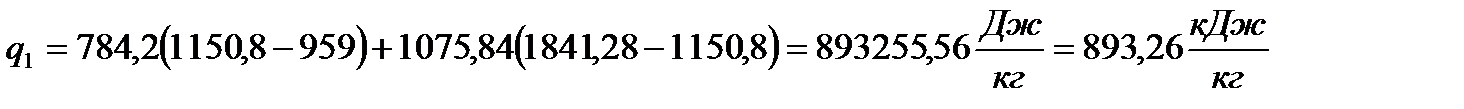
Определяю количество отведённой теплоты ( 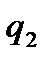 , кДж/кг) по формуле
, кДж/кг) по формуле
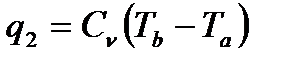 (25)
(25)
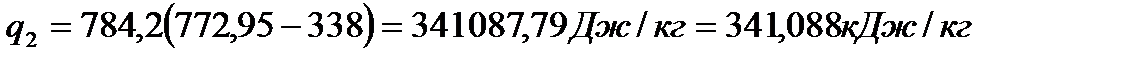 .
.
5. Сравнение расчётного термического КПД с его значением, определённым через подведённую и отведённую теплоту, а так же с КПД цикла Карно
Термический КПД цикла через подведённую и отведённую теплоту определяется по формуле
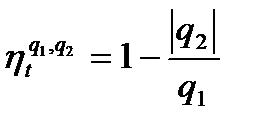 (26)
(26)
Подставляя известные величины в формулу (26), получаю
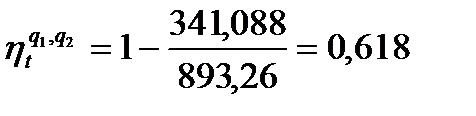
или 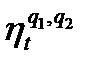 =61,8%.
=61,8%.
Термический КПД цикла Карно нахожу по формуле
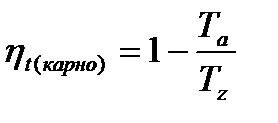 (27)
(27)
где 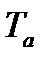 и
и 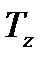 - минимальная и максимальная температура цикла, К.
- минимальная и максимальная температура цикла, К.
Подставляя известные величины в формулу (27), получаю
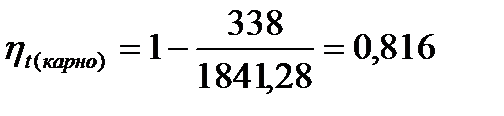
или 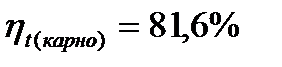 .
.
Сравниваю полученные КПД:
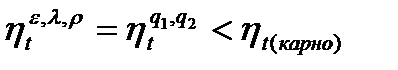 ; (28)
; (28)
0,618=0,618<0,816.
6. Определяю работу по процессам цикла и суммарную работу за цикл
Так как процесс (a-с) адиабатный, то работа определяется по формуле
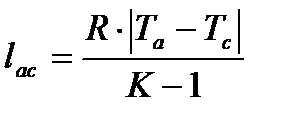 (29)
(29)
Подставляя известные значения в формулу, получаю
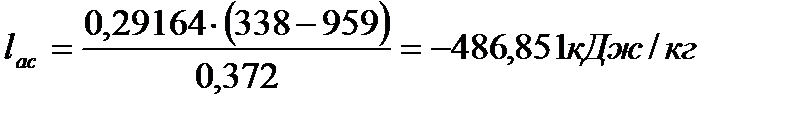
Так как процесс (c-z’) изохорный, то 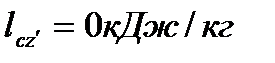 ,
,
Процесс (z’-z) изобарный, и работа определяется по формуле
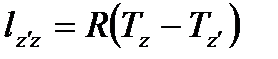 (30)
(30)
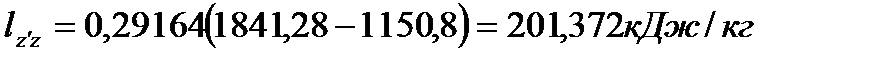
Процесс (z-b) адиабатный, как и процесс (a-c). Поэтому, справедлива формула
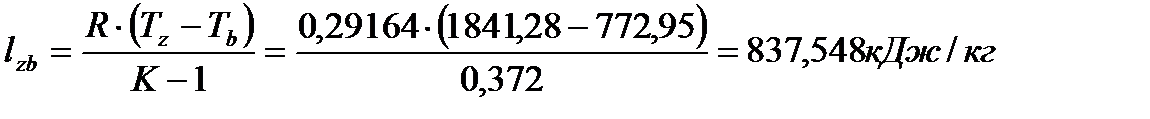 (31)
(31)
Процесс (b-a) изохорный, значит 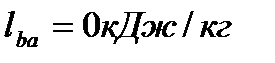 .
.
Работа за цикл будет складываться из всех работ процессов цикла по формуле
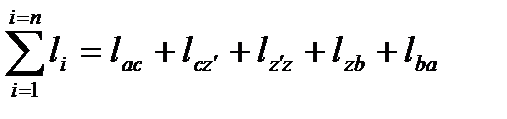 (32)
(32)
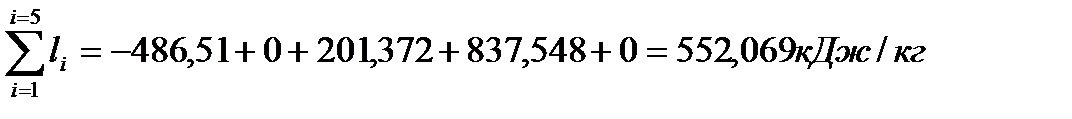 .
.
7. Определение полезной и максимальной (эксергии) работы цикла. Сравнение максимальной работы с суммарной работой по процессам цикла.
Полезная работа находится по формуле
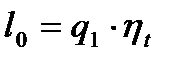 . (33)
. (33)
Подставляя известные величины в формулу (33), получаю
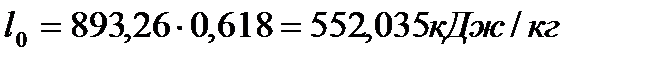 .
.
Максимальная полезная работа определяется по формуле
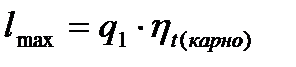 . (34)
. (34)
Подставляя известные значения в формулу (34), получаю
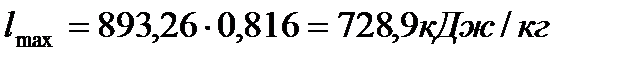 .
.
Сравнивая работы за цикл, получаю, что
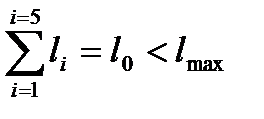 (35)
(35)
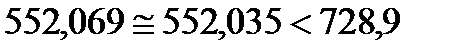
Относительная ошибка в процентах составит
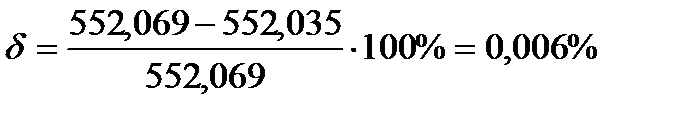 , что допустимо.
, что допустимо.
8. Определяем изменение внутренней энергии, энтальпии и энтропии рабочего тела по процессам цикла и в целом за цикл.
8.1. Изменение внутренней энергии находится по формуле
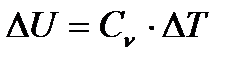 , (36)
, (36)
где 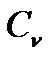 - удельная теплоёмкость смеси при
- удельная теплоёмкость смеси при 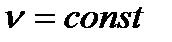 Дж/(кг
Дж/(кг  К);
К);
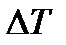 - изменение температуры процесса, К
- изменение температуры процесса, К
Применяя эту формулу для каждого цикла, получаю
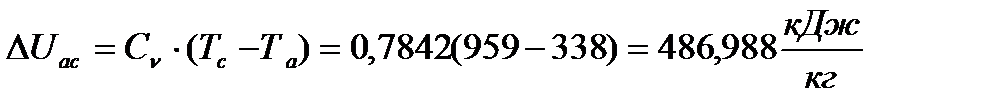 (37)
(37)
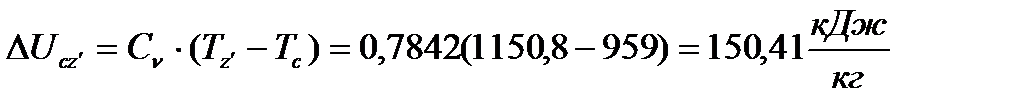 (38)
(38)
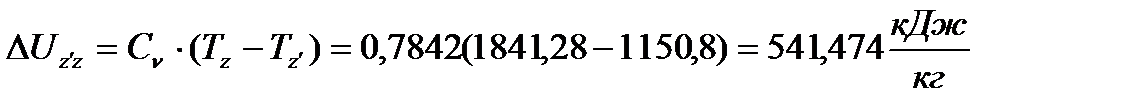 (39)
(39)
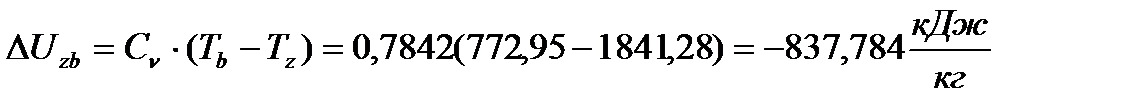 (40)
(40)
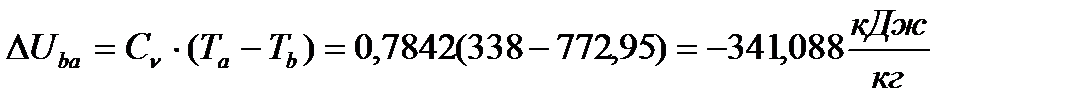 (41)
(41)
Изменения внутренней энергии за цикл будут равны
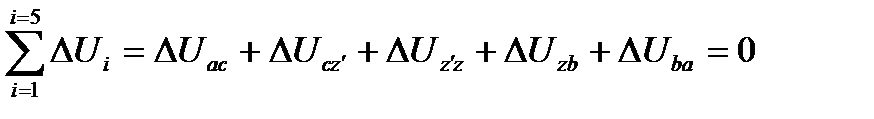 (42)
(42)
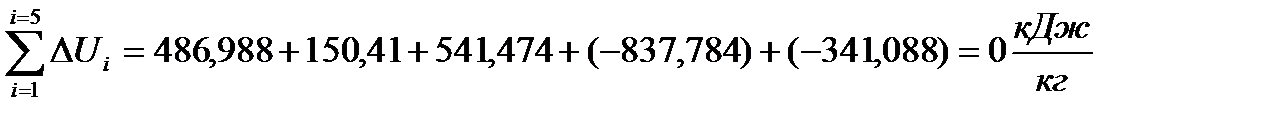
8.2 Изменение энтальпии по процессам цикла определяется по формуле
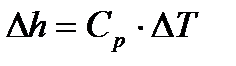 , (43)
, (43)
где 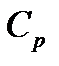 - удельная теплоёмкость смеси при p=const, кДж/кг.
- удельная теплоёмкость смеси при p=const, кДж/кг.
Подставляя известные величины в формулу (43), получаю
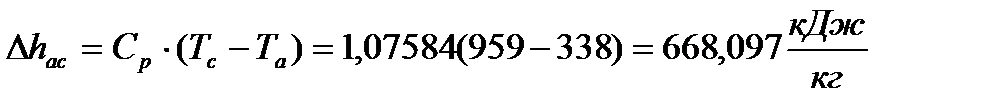 (44)
(44)
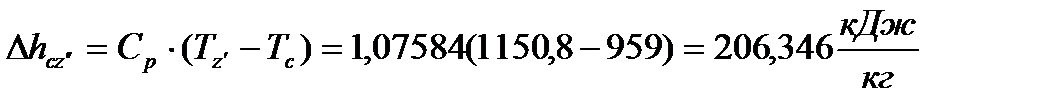 (45)
(45)
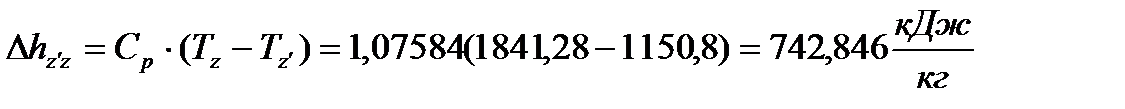 (46)
(46)
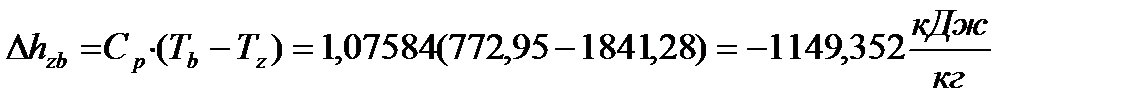 (47)
(47)
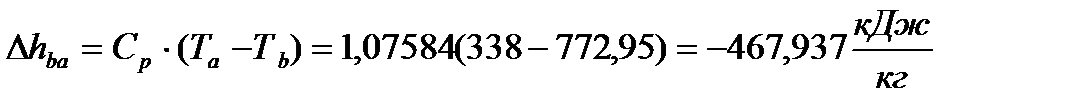 (48)
(48)
Изменения энтальпии за цикл будут равны сумме изменений энтальпии по процессам
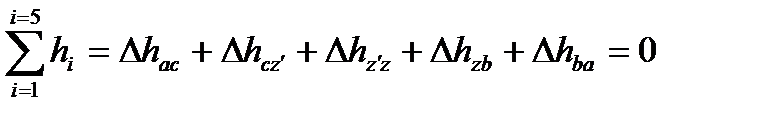 (49)
(49)
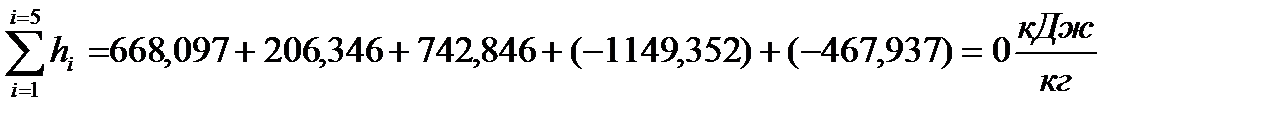
8.3 Находим изменения энтропии по процессам.
Так как процессы (a-c) и (b-z) адиабатные, отсюда следует, что
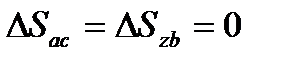 , т.к. q=0,
, т.к. q=0, 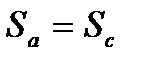
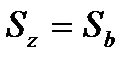
Процесс 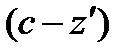 изохорный, поэтому
изохорный, поэтому
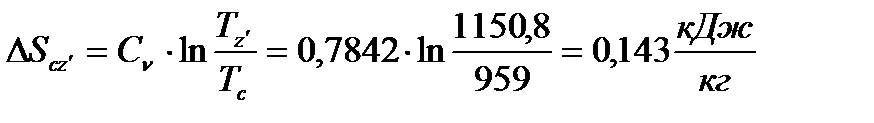 (50)
(50)
Процесс 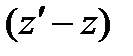 изобарный, поэтому
изобарный, поэтому
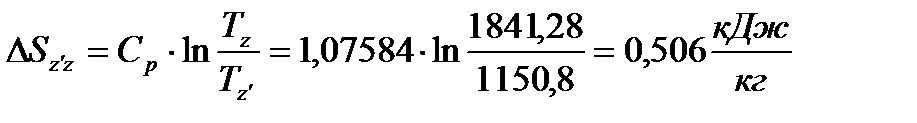 (51)
(51)
Процесс (b-a) изохорный, поэтому
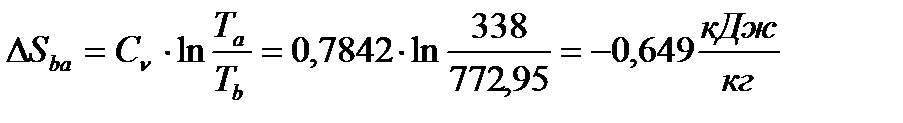 (52)
(52)
Изменения энтропии за цикл будут равны сумме изменений энтропии по процессам
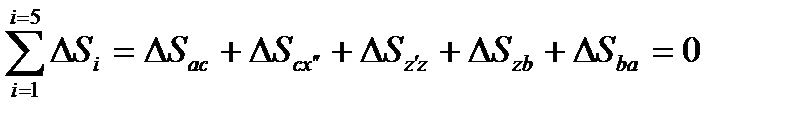 (53)
(53)
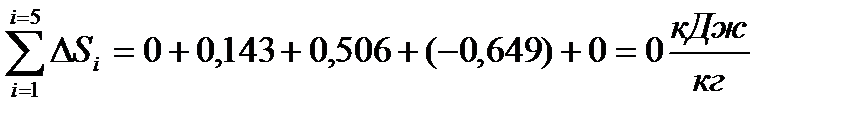
9. Оценка применимости первого закона термодинамики к процессам цикла и в целом за цикл.
Первый закон термодинамики имеет вид
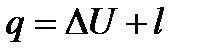 (54)
(54)
Применяя эту формулу для процессов цикла, получаю:
а) адиабатный процесс (a-c)
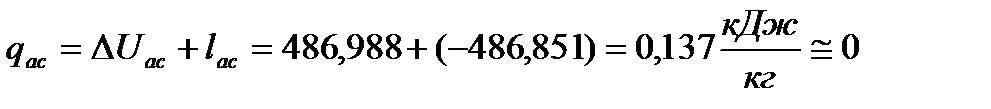 (55)
(55)
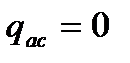 , тогда
, тогда 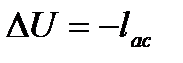 или
или 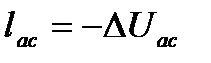 ;
;
б) изохорный процесс 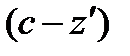
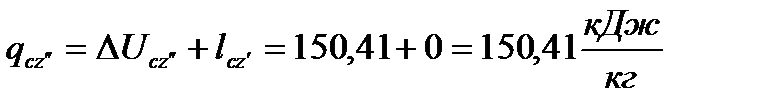 (56)
(56)
Тогда
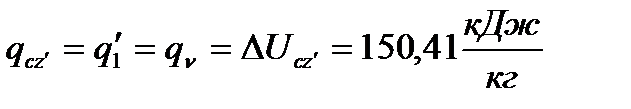 (57)
(57)
в) изобарный процесс 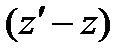
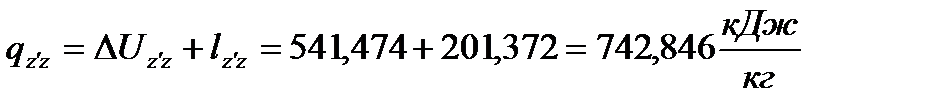 (58)
(58)
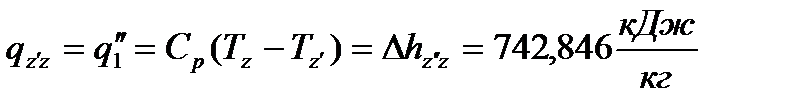 ; (59)
; (59)
г) адиабатный процесс (z-b)
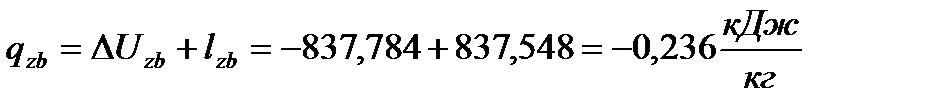 (60)
(60)
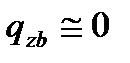 , тогда
, тогда 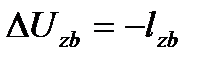 или
или 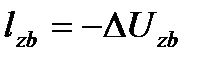
д) изохорный процесс (b-a)
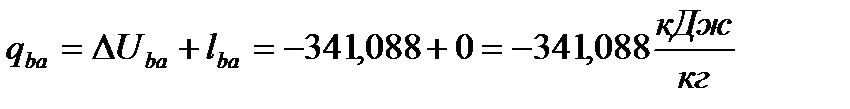 (61)
(61)
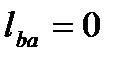 ,
,
Тогда
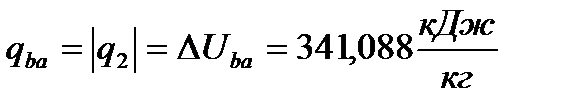 (62)
(62)
В целом за цикл
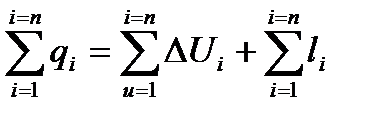 ; (63)
; (63)
Тогда
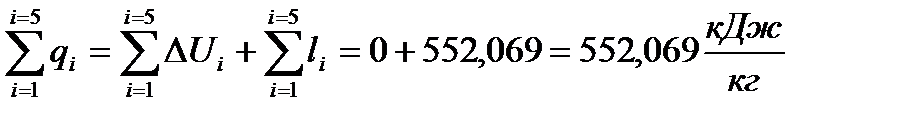 (64)
(64)
или
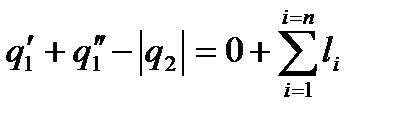 (65)
(65)
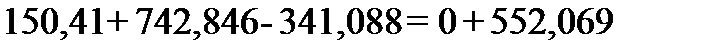
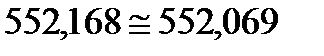 ;
;
Тогда
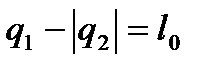
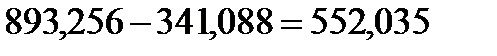
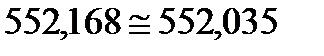 .
.
10. Определение среднего индикаторного давления по параметрам цикла и полезной работы цикла.
Среднее индикаторное давление по параметрам цикла определяю по формуле
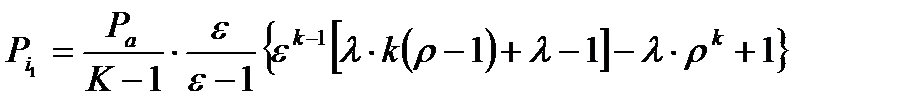 , (66)
, (66)
где ρ - степень предварительно расширения, ρ=1,6;
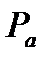 - давления в начале сжатия, МПа
- давления в начале сжатия, МПа
Подставляя известные значения в формулу (66), получаю
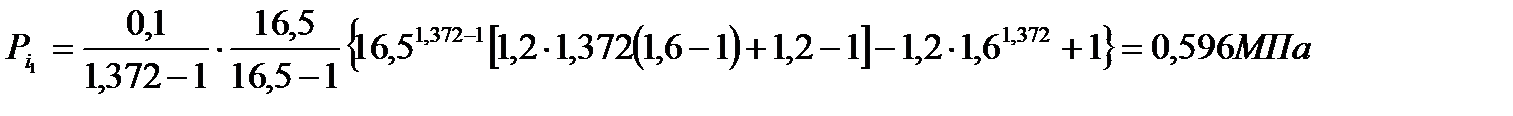
Среднее индикаторное давление по полезной работе цикла определяется по формуле
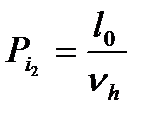 , (67)
, (67)
где  - рабочий объём,
- рабочий объём, 
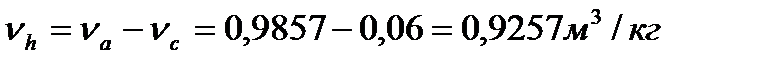 (68)
(68)
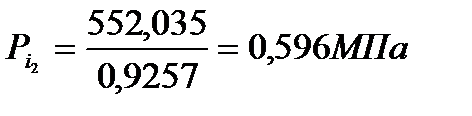 .
.
Из расчётов видно, что
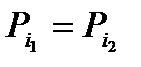
 .
.
11. Построение цикла в P-ν и T-s диаграммах
По вычисленным значениям давлений и удельных объёмов в характерных точках изображается идеальный цикл в p-ν координатах. Адиабаты сжатия и расширения проводятся (плавные кривые) с использованием промежуточных точек, которые определяются из уравнений:
11.1 Построение цикла в P-ν-диаграмме
а) адиабата (a-c)
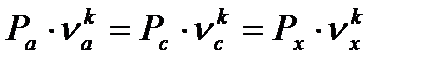 (69)
(69)
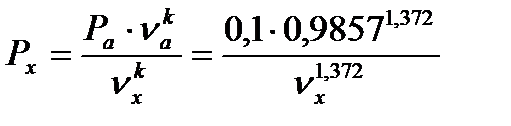 (70)
(70)
При 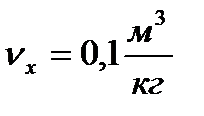
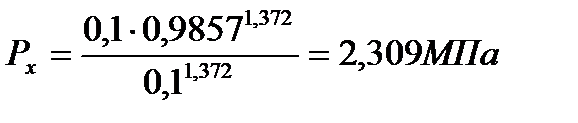
При 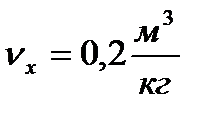
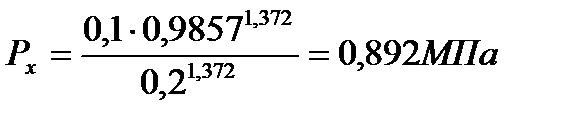
При 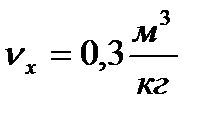
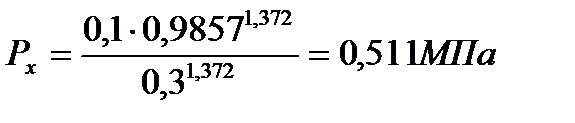
При 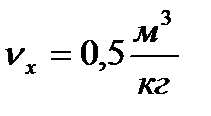
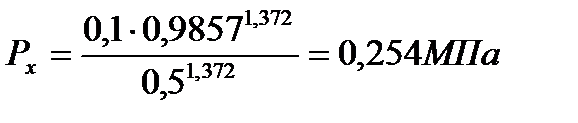
При 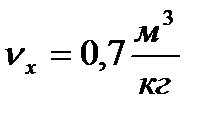
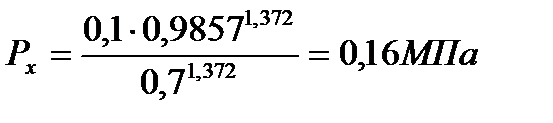
При 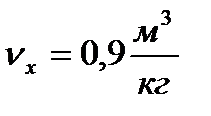
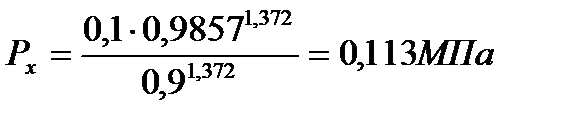
б) адиабата (z-b)
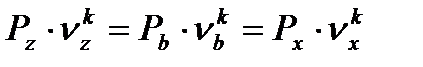 (71)
(71)
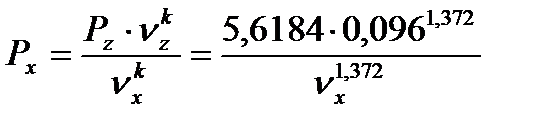 (72)
(72)
При 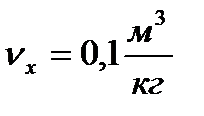
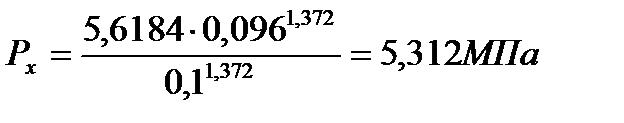
При 
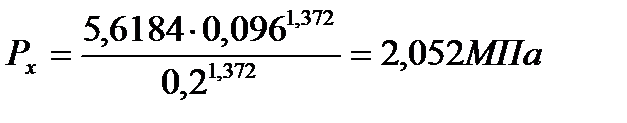
При 
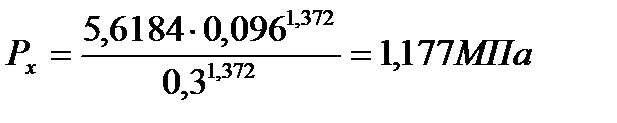
При 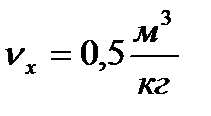
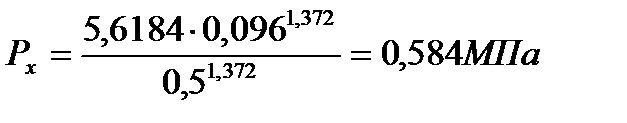
При 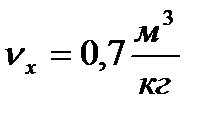
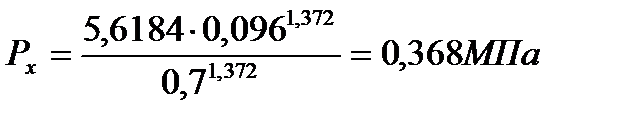
При 
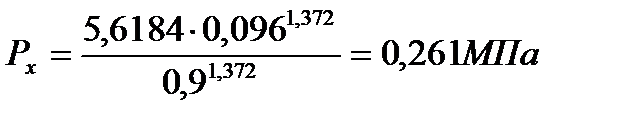
Расчётные параметры P и ν в характерных и промежуточных точках свожу в таблицы 1 и 2.
Таблица 1 – Параметры P и ν в характерных точках.
| Точки цикла | a | c | 
| z | b |
| P, МПа | 0,1 | 4,682 | 5,6184 | 5,6184 | 0,2287 |
ν, 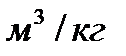
| 0,9857 | 0,06 | 0,06 | 0,096 | 0,9857 |
Таблица 2 – Параметры P и ν в промежуточных точках.
| Промежуточные точки | 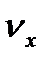 , , 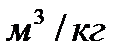
| 0,1 | 0,2 | 0,3 | 0,5 | 0,7 | 0,9 |
| (a-c) | 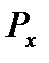 , МПа , МПа
| 2,309 | 0,892 | 0,511 | 0,254 | 0,16 | 0,113 |
| (z-b) | 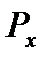 , МПа , МПа
| 5,312 | 2,052 | 1,177 | 0,584 | 0,368 | 0,261 |
11.2 Построение цикла в T-s-диаграмме.
Для построения цикла в диаграмме T и s необходимо определить начальное значение энтропии по формуле
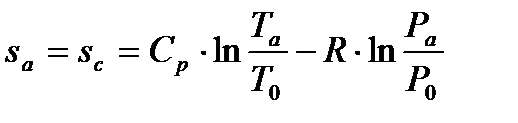 , (73)
, (73)
где 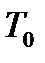 =273 К,
=273 К,
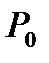 =760 мм.рт.ст.=0,101325 МПа
=760 мм.рт.ст.=0,101325 МПа
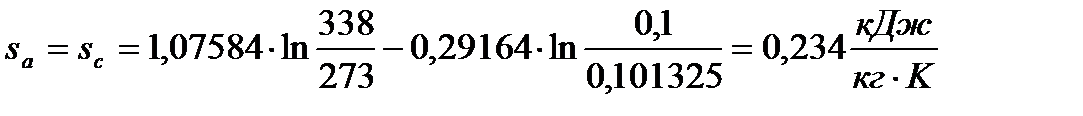
Значения энтропии в характерных точках определяются по формулам
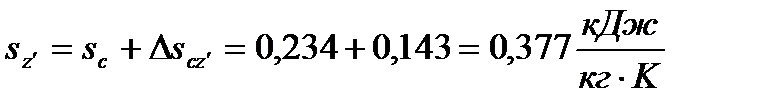 (74)
(74)
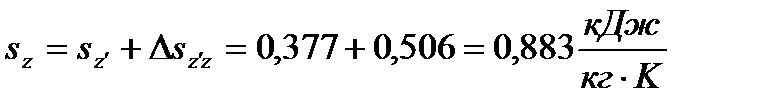 (75)
(75)
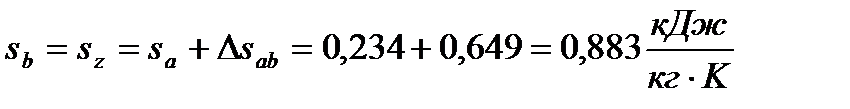 (76)
(76)
Данные расчётов свожу в таблицу 3.
Таблица 3 – Параметры T и s в характерных точках
| Точки цикла | a | c | 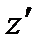
| z | b |
| T,K | 1150,8 | 1841,28 | 772,95 | ||
| s, кДж/кгK | 0,234 | 0,234 | 0,377 | 0,883 | 0,883 |
Построение изохор и изобары в T-s-диаграмме производится также по промежуточным точкам.
Для определения промежуточных точек изохоры (с-z’) используется формула
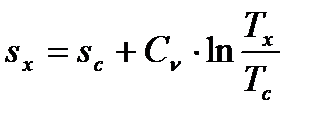 , (77)
, (77)
где 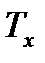 - произвольно взятая температура из условия
- произвольно взятая температура из условия 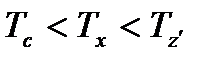 , К.
, К.
При 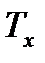 =1000К
=1000К
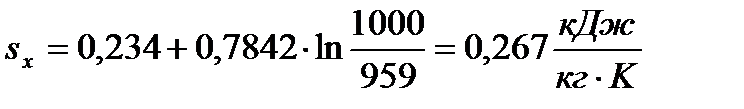
При 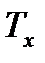 =1050К
=1050К
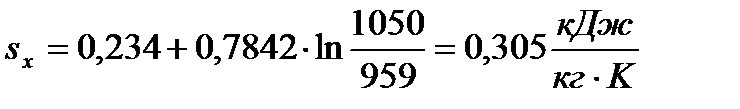
При 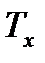 =1100К
=1100К
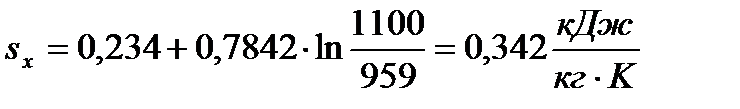
Для определения промежуточных точек изобары (z-z’) используется формула
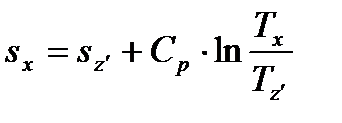 , (78)
, (78)
где 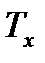 - произвольно взятая температура из условия
- произвольно взятая температура из условия 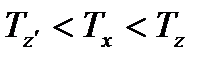 , К.
, К.
При 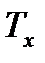 =1200К
=1200К
При 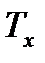 =1400К
=1400К
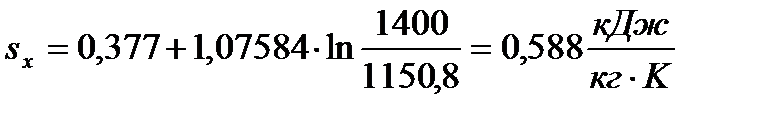
При 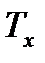 =1600К
=1600К
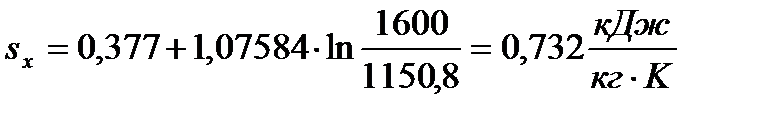
При 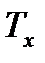 =1800К
=1800К
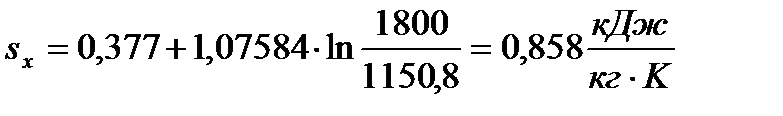
Для определения промежуточных точек изохоры (a-b) используется формула
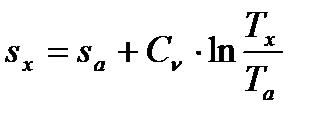 , (79)
, (79)
где 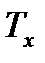 - произвольно взятая температура из условия
- произвольно взятая температура из условия 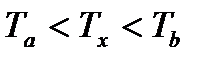 , К.
, К.
При 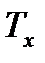 =400К
=400К
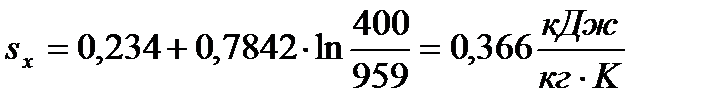
При 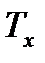 =500К
=500К
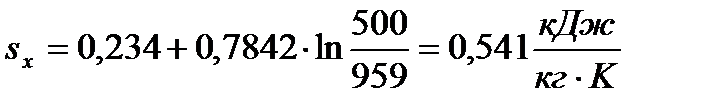
При 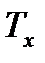 =600К
=600К
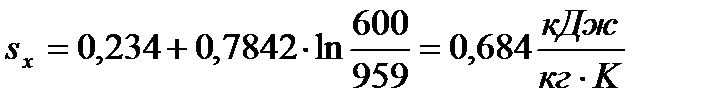
При 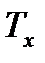 =700К
=700К
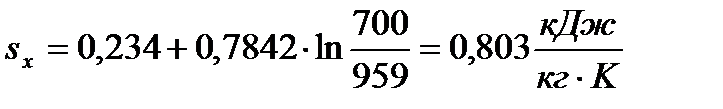
Данные расчёта свожу в таблицу 4.
Таблица 4 – Значения параметров промежуточных точек для построения изохор и изобары в T-s-диаграмме.
| Процесс | Условия | Значение | ||||
| Изохора c-z’ |
| 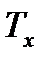 ,K ,K
| ||||
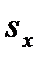 ,кДж/кгК ,кДж/кгК
| 0,267 | 0,305 | 0,342 | |||
| Изобара z’-z |
| 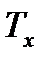 ,K ,K
| ||||
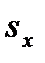 ,кДж/кгК ,кДж/кгК
| 0,422 | 0,588 | 0,732 | 0,858 | ||
| Изохора a-b (b-a) |
| 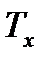 ,K ,K
| ||||
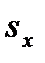 ,кДж/кгК ,кДж/кгК
| 0,366 | 0,541 | 0,684 | 0,803 | ||
Теперь выбираю масштаб для p-ν-диаграммы
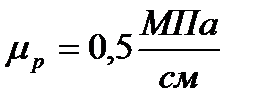
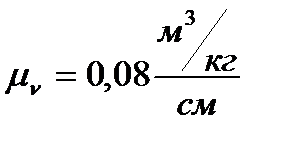
Тогда для того, чтобы построить p-ν-диаграмму каждое число из таблицы 1 и 2 делим на 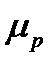 и
и 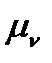 .
.
Выбираю масштаб для T-s-диаграммы
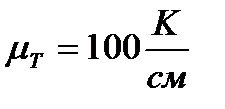
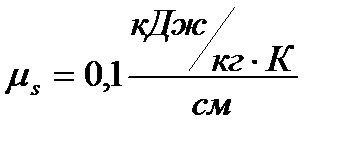 .
.
Для того, чтобы построить T-s-диаграмму каждое число из таблиц 3 и 4 делим на 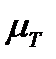 и
и 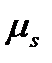 .
.
12. Определение площади цикла, эквивалентной полезной работе и указание на P-ν-диаграмме среднего индикаторного давления.
Площадь цикла 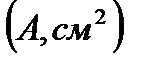 , эквивалентная полезной работе цикла, определяется по формуле
, эквивалентная полезной работе цикла, определяется по формуле
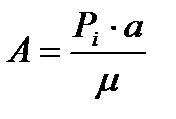 , (80)
, (80)
где 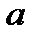 - длина проекции цикла на ось удельного объёма, см;
- длина проекции цикла на ось удельного объёма, см;
µ - масштаб давления, 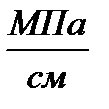 .
.
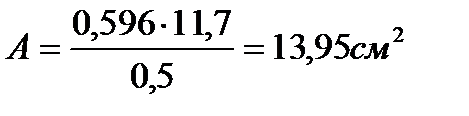
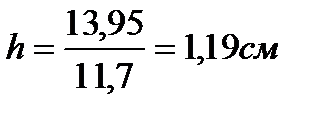
В P-ν-диаграмме полезная работа цикла изображается в виде прямоугольника, равного площади цикла, с основанием рабочего объёма и высотой, равной среднему индикаторному давлению.
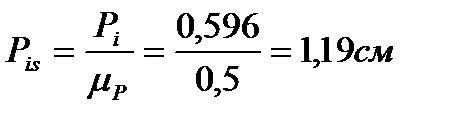
Заключение.
В ходе выполнения курсовой работы было установлено следующее:
1. Расчёт проводился для цикла бескомпрессорного дизельного двигателя со смешанным подводом теплоты. Определены такие параметры рабочего тела в характерных точках цикла, как температура, давление и удельный объём.
2. Значение термического КПД двигателя по параметрам цикла составило 0,618, что одновременно соответствует значению данного показателя, определённым через подведённую и отведённую теплоту. Сравнение термического КПД двигателя с КПД цикла Карно определяется неравенством 0,618<0,816.
3. Расчётные значения полезной и максимальной (эксергии) работы цикла соответственно составляют: 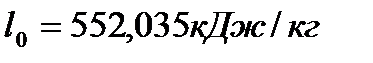 и
и 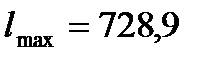 кДж/кг. Сравнение максимальной работы с суммарной работой по процессам цикла соответствует неравенству 552,069<728,9. Относительная ошибка между суммарным значением работы по процессам цикла и полезной работой за цикл составляет 0,006%, что допустимо.
кДж/кг. Сравнение максимальной работы с суммарной работой по процессам цикла соответствует неравенству 552,069<728,9. Относительная ошибка между суммарным значением работы по процессам цикла и полезной работой за цикл составляет 0,006%, что допустимо.
4. Проведены расчёты по определению изменения внутренней энергии, энтальпии и энтропии по процессам цикла и в целом за цикл. Равенства: 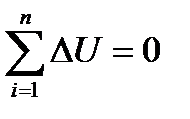 ,
, 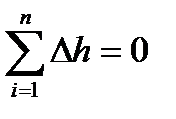 и
и 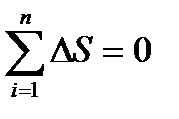 подтверждают правильность расчёта.
подтверждают правильность расчёта.
5. Применимость первого закона термодинамики к процессам цикла и в целом за цикл определяется соотношением 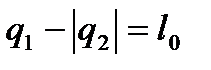 и по результатам расчётов составляет
и по результатам расчётов составляет 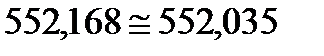 , что допустимо.
, что допустимо.
6. Расчётные значения среднего индикаторного давления по параметрам цикла и по полезной работе за цикл соответственно составляют: 0,596=0,596 МПа.
7. По результатам построения P-ν-диаграммы, для цикла бескомпрессорного дизельного двигателя со смешанным подводом теплоты, площадь цикла, эквивалентная полезной работе, равна 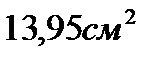 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
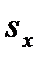 в зависимости от
в зависимости от