Хелпикс

Главная

Контакты

Случайная статья



Исходные данные



 

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ИНСТИТУТ ЭНЕРГЕТИКИ И ТРАНСПОРТНЫХ СИСТЕМ

КАФЕДРА: «ТУРБИНЫ, ГИДРОМАШИНЫ И АВИАЦИОННЫЕ ДВИГАТЕЛИ»

 

Вычислительная лабораторная работа №1

Расчет течения в начальном участке плоского канала

 

 

Выполнил: студент гр. 53222/13

Нянченков А.И.

 

Проверил: преподаватель

Китанина Е. Э.

 

 

Санкт-Петербург

Исходные данные

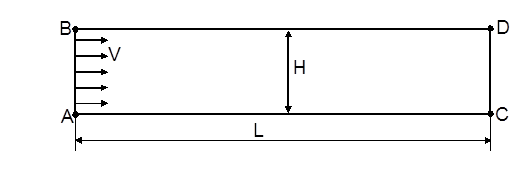
Рис. 1. Расчетная область для исследования начального участка плоского канала

На рисунке представлена расчетная область – плоский канал ABCD высотой Н и длиной L с числом калибров L/H = 20. Границами расчетной области служат ребро AB – вход в канал, ребра AD и BC – стенки канала, ребро CD – выход из канала. Через границу AB подается однородный поток со скоростью U=1. Течение определяется одним безразмерным режимным параметром – числом Рейнольдса Re = U×H/n, здесь n – кинематический коэффициент вязкости, U – масштаб скорости, H – линейный масштаб. Поскольку величина H выбрана в качестве масштаба, то AB = 1, AD = 20.

При выполнении задания следует использовать одноблочные исходную и измельченную сетки с неравномерным распределением узлов. Сетки сгущаются у стенок канала и в окрестности входа. Количество узлов на сегментах (каждое ребро состоит из одного сегмента) и коэффициенты сгущения для исходной сетки задаются в соответствии со значениями, приведенными в таблице:

Сегмент AB, CD AD, BC
Число узлов Jmax = 21 Imax = 61
Коэффициент сгущения 1.1 по направлению к стенкам 1.07 к началу канала

Задача решается в безразмерной постановке для трех ламинарных режимов течения: Re = 100, 200, 400. Значению Re = 100, например, соответствует течение воды (n = 10‑6 м2/с) в канале шириной 0.01 м при входной скорости 0.1 м/с. На входе в канал задается однородный профиль безразмерной скорости U = 1, V = 0. На выходной границе задается нормированное давление P = 0.

Для режима Re = 100 следует провести анализ сеточной зависимости получаемого решения, решив задачу на сетке, измельченной в два раза по каждому индексному направлению.

Расчеты следует выполнять по методу AC/SIMPLEC при значении числа Куранта CFL = 10. Следует также задать ненулевое начальное значение для поля продольной компоненты скорости (UINIT = 0.1).

Задачи

Выполнить расчет стационарного ламинарного течения несжимаемой жидкости в начальном участке плоского канала для разных значений числа Рейнольдса; сопоставить расчетные длину начального участка и коэффициент сопротивления развитого течения с результатами аналитического решения.

 

1) Проанализировать векторные поля скорости и скалярные распределения компонент скорости, сравнить между собой однотипные картины для разных режимов;

2) с помощью программы EasyCut подготовить данные, а с помощью Excel построить и сопоставить профили скорости в четырех сечениях канала: на входе, на расстоянии примерно половины калибра (ширины канала) от входа, примерно в середине начального участка и на участке развитого течения;

3) оценить длину начального участка канала (в качестве границы начального участка следует выбрать сечение, в котором значение максимальной скорости составляет 98% от максимальной скорости развитого течения Umax = 1.5Uвх); провести сопоставление полученных результатов по длине начального участка с аналитическим решением Lнач/H = 0.04×Re [1]; представить результаты в виде таблицы и графически;

4) проанализировать поле нормированного давления; найти коэффициент сопротивления  l для начального участка, участка с установившимся параболическим профилем скорости и канала в целом при помощи формулы [2]

,

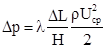где Dp – перепад давления на участке канала длиной DL, r=1 – плотность жидкости, Uср=1 – средняя по сечению скорость. Построить график зависимости давления на оси канала от продольной координаты. Определить значение l для участка развитого течения из угла наклона линейного участка зависимости. Провести сопоставление с теоретической оценкой для развитого участка l = 24/Re [2]; представить результаты в виде таблицы и графически.

5) Построить график зависимости коэффициента трения на стенке канала, Cf, от координаты x. Распределение коэффициента трения следует извлечь из файла <prefix>*.sf?, где * соответствует номеру сохраненного решения, а расширение зависит от построенной сетки (обычно это sf3); файл размещен в подпапке «Case_data» папки проекта. Убедиться в том, что для участка развитого течения выполняется соотношение l = 2 Cf.

1. Анализ полученных картин для разных режимов течения

Re = 100

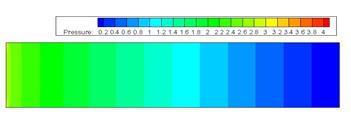
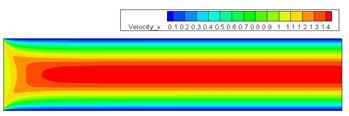
Рис. 2. Скалярное распределение давления                      Рис. 3. Скалярное распределение x-компоненты скорости

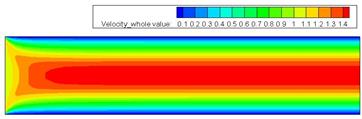
Рис. 4. Скалярное распределение y-компоненты скорости    Рис. 5. Скалярное распределение полной скорости

Re = 200

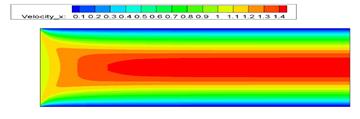
Рис. 6. Скалярное распределение давления                   Рис. 7. Скалярное распределение x-компоненты скорости:

 

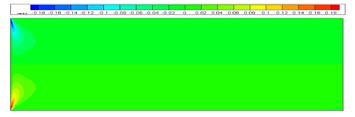
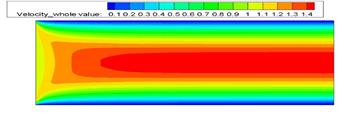
Рис. 8. Скалярное распределение y-компоненты скорости Рис. 9. Скалярное распределение полной скорости

 

Re = 400

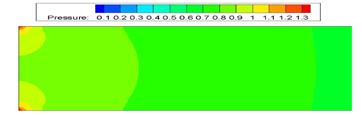
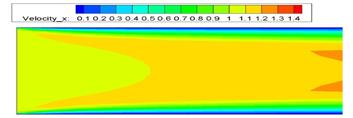
Рис. 10. Скалярное распределение давления               Рис. 11. Скалярное распределение x-компоненты скорости:

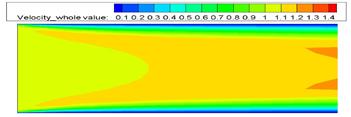
Рис. 12. Скалярное распределение y-компоненты скорости Рис. 13. Скалярное распределение полной скорости

При большем числе Рейнольдса величина скорости на начальном участке канала в середине линии тока меньше, чем при малом числе Рейнольдса, похожий процесс происходит и с давлением, чем больше число Рейнольса, тем меньше перепад давления в канале. Y составляющая скорости практически неизменна.

 

2. Сопоставление профилей скорости в разных сечениях канала

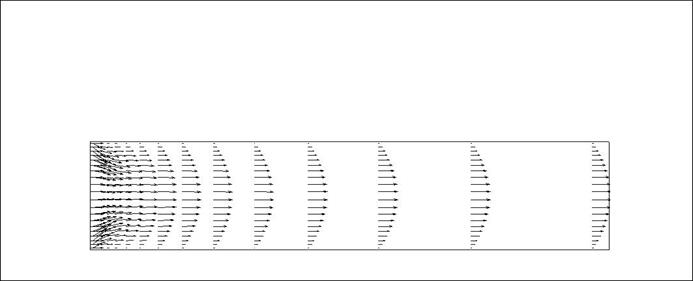
Рис. 14. Векторное поле скорости: при Re = 100

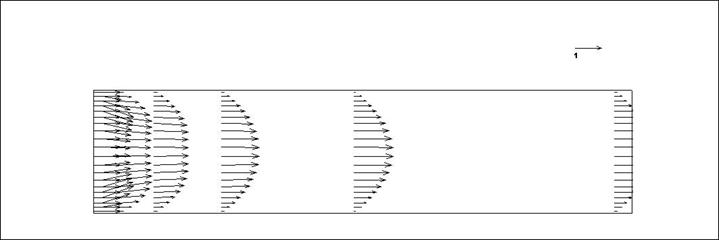
Рис. 15. Векторное поле скорости: при Re = 200

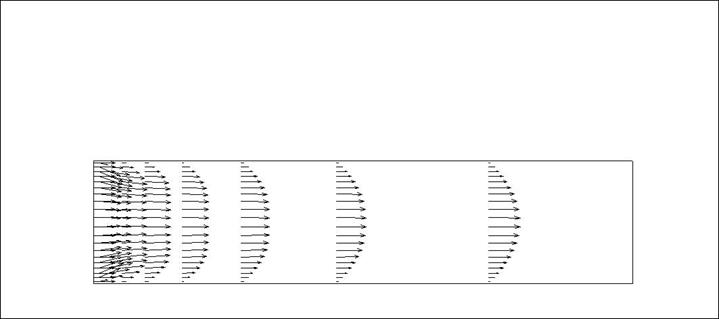
Рис. 16. Векторное поле скорости: при Re = 400

На рис. 14-16 можно увидеть , что на входе в канал профиль скорости постоянен, но уже на 12% длинны канала приобретает параболический вид . Это связано со стабилизацией потока. Т.к на входе в канал силы трения оказывают не большое влияние , но на 3% длинны канала они начинают сказываться . У стенок скорость равна нулю, в ядре потока она максимальна и соединив три точки мы получим параболу.

 

3. Оценка длины начального участка

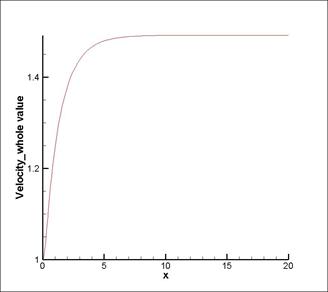
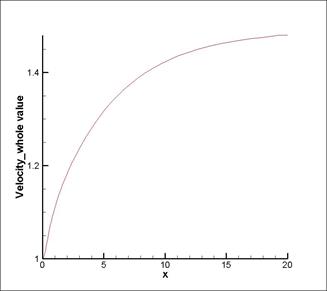
Рис. 17. Эпюра скорости: Re = 100                       Рис. 19. Эпюра скорости: Re = 400

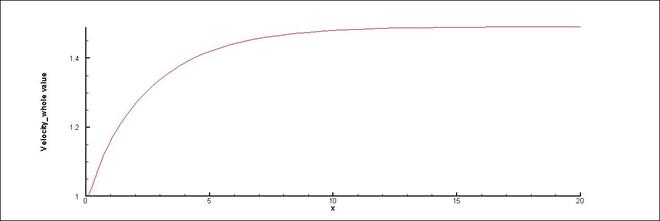
Рис. 18. Эпюра скорости: Re = 200

Из выше представленных рисунков видно, что чем больше число Рейнольдса тем больше длинна начального участка.

 Таблица 1. Длины начальных участков.

Re 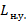Lнач/H = 0.04×Re
100 4,24 4
200 8,266 8
400 16,25 16

Вышеизложенный вывод так же подтверждается эмпирическими расчетами.

 

4. Анализ полей нормированного давления

Таблица 2. Коэффициенты сопротивления для начального участка, участка с развитым течением и канала в целом.

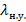
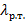
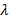
Re l = 24/Re
100 0,36 0,24 0,265 0,24
200 0,186 0,121 0,148 0,12
400 0,131 0,062 0,188 0,06

 

Данные, полученные в результате математического и эмпирического анализа свидетельствуют о том, что при увеличении числа Рейнольдса коэффициенты сопротивления уменьшаются на начальном участке, участке с развитым течением и на всей длине канал

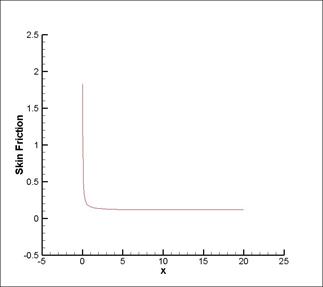
5. График зависимости коэффициента трения на стенке канала Cf, от координаты x

Re=100

 

 

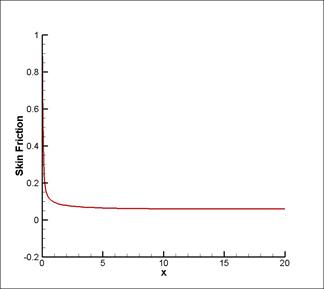
Re=200

Re=400

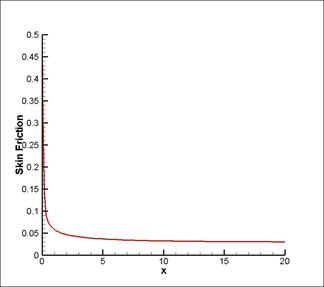
Рис. 20. График зависимости коэффициента трения на стенке канала Cf, от координаты x

Проанализировав поле нормированного давления, определили значение l для участка развитого течения из угла наклона линейного участка зависимости. Провели сопоставление с теоретической оценкой для развитого участка, и получили расхождение при числе Рейнольдса =100 в 0,08%, при числе Рейнольдса =200 в 1,42%, при числе Рейнольдса =400 в 4,83%. Во всех случаях расхождение в большую сторону.

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.