
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача № 3.
Задача № 3.
По горизонтально расположенной стальной трубе (λ = 20 Вт/(м‧К)) со скоростью W = 2.1*10 м/с течет вода, имеющая температуру tв = 160 °С. Снаружи труба охлаждается окружающим воздухом, температура которого tвоз = 16 °С, давление Р = 0,1 МПа.
Определить:
· коэффициенты теплоотдачи α1 и α2 соответственно от воды к стенке трубы и от стенки трубы к воздуху;
· коэффициент теплопередачи и тепловой поток q, отнесенный к 1 м длины трубы, если внутренний диаметр трубы равен d1 = 180 мм,
внешний d2 = 200 мм.
Для определения α2 принять в первом приближении температуру наружной поверхности трубы t2 равной температуре воды.
Ответить на вопросы:
1. Какой режим течения внутри трубы в вашем варианте задачи?
2. Какой режим движения окружающего трубу воздуха?
3. Почему можно при расчете принять равенство температур t2 = tв?
Решение.
1. Определяем коэффициент теплоотдачи от воды к стенке трубы
При tв = 160С определяем параметры воды:
- коэффициент теплопроводности λ = 20 Вт/(м*К);
- коэффициент кинематической вязкости ν = 0,191*10-6 м2 /с;
- число Прандтля Pr = 1,1 (приложение2)
Число Рейнольдса:
Критерий Рейнольдса Re = w * d1 / ν = 0,19 * 0,18 / (0,191* 10-6) = 179 057
Так как Re1 > 104, режим движения воды – турбулентный, критериальное уравнение для определения числа Нуссельта (горизонтальная труба) имеет вид:
Nu = 0,021* Re 0,8 * Pr 0,43 (Prж /Prс)0,25 = 0,021* 179 0570,8 * 1,10,43 (1,1/1,1)0,25 =348,6.
Коэффициент теплоотдачи:
α1 = Nu * λ / d1 = 348,6 * 0,683/0,18 =1 322 Вт/(м2*К).
2. Определяем коэффициент теплоотдачи от стенки трубы к воздуху
При tвозд = 16 0С определяем параметры воздуха:
- коэффициент теплопроводности λ = 0,02593 Вт/(м*К);
- коэффициент кинематической вязкости ν = 15,06*10-6 м2/с;
- число Прандтля Pr = 0,703.
Определяем число Грасгофа:
Gr = g * d23 * β * ∆t/ν2,
∆t = tв – tвозд = 160 – 16 = 144 0C, β = 1 / Tвозд = 1/289 =3,4*10-3 1/К.
Gr = 9,81* 0,23 * 3,4 * 10-3 * 144 / (15,06 * 10-6)2 = 169 414 453.
Для горизонтальной трубы критериальное уравнение для определения числа Нуссельта:
Nu = 0,5*(Gr*Pr)0,25 = 0,5*(169 414 453 * 0,703)0,25 = 52,2
Получаем: α2 = Nu*λ / d2 = 52,2*0,02593/0,2 = 6,76Вт/м2*К
3. Коэффициент теплопередачи от воды к воздуху, через цилиндрическую стенку:
k = [1 / (d1 * α1) + (1 / 2λ) * ln (d2 / d1) +1 / (α2 * d2)),
где d1 – внутренний диаметр трубы , d1 = 180 мм;
d2 – наружный диаметр трубы, d2 = 200 мм;
λ – коэффициент теплопроводности материала трубы, λ = 20 Вт/(м*К).
k = (1/(0,18 * 1322) + (1 / 2*20)*ln(0,2/0,18) +1/(6,76 * 0,2)) = 0,74 Вт/(м2*К).
Погонный тепловой поток:
q1 = k * π * ( tв – tвоз) = 0,74* 3,14*(160 – 16) = 334,6 Вт/м.
Ответить на вопросы:
1. Какой режим течения внутри трубы?
Так как Re1 =3,28*105 > 0, режим течения внутри трубы – турбулентный
2. Какой режим движения окружающего трубу воздуха?
Снаружи трубы – свободная конвекция.
3. Почему при расчёте можно принять равенство температур стенки и воды?
Стенка выполнена из стали с высоким коэффициентом теплопроводности,
также коэффициент теплоотдачи от воды к стенке имеет высокое значение.
Поэтому при расчётах можно принять равенство температур стенки и воды.
Задача №4
Определить поверхность нагрева рекуперативного газо-воздушного теплообменника при прямоточной и противоточной схемах движения теплоносителей, если объемный расход нагреваемого воздуха при нормальных условиях Vн=5*10-3 м3/ч, средний коэффициент теплопередачи от продуктов сгорания к воздуху К=22 Вт/м2к, начальные и конечные температуры продуктов сгорания и воздуха соответственно tʹ1=625, t”1=425, t’2=15, t”2=325. Изобразить графики изменения температур теплоносителей для обеих схем движения теплоносителей.
Комментарий к расчету задачи №4
Рекуперативный газо-воздушный теплообменник может иметь различное конструктивное исполнение. Независимо от конструкции поверхность нагрева теплообменника определяется с помощью двух уравнений: теплового баланса и теплопередачи.
Расчет.
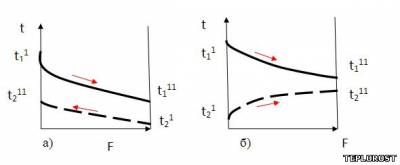
Рисунок 1 – Схемы движения теплоносителей в теплообменниках:
а – противоток; б - прямоток
Массовый расход воздуха
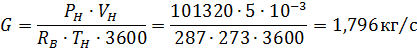
Где 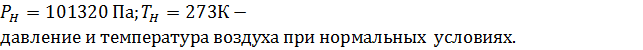
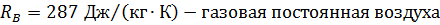
Тепловой поток 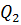 , получаемый холодным воздухом, можно рассчитать через разность энтальпий
, получаемый холодным воздухом, можно рассчитать через разность энтальпий
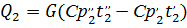
Где 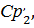
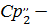 теплоемкость воздуха при соответствующих температурах
теплоемкость воздуха при соответствующих температурах
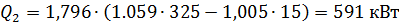
Противоточная схема
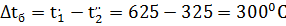
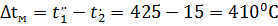
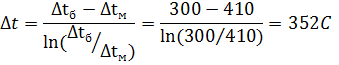
Площадь поверхности нагрева

Прямоточная схема
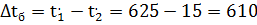
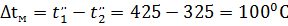
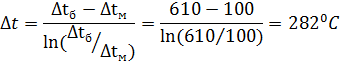
Площадь поверхности нагрева
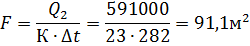
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|