Контакты

Случайная статья

Нахождение Ѳ в точках. Температура в точках через 25 мин после посада заготовки в печь

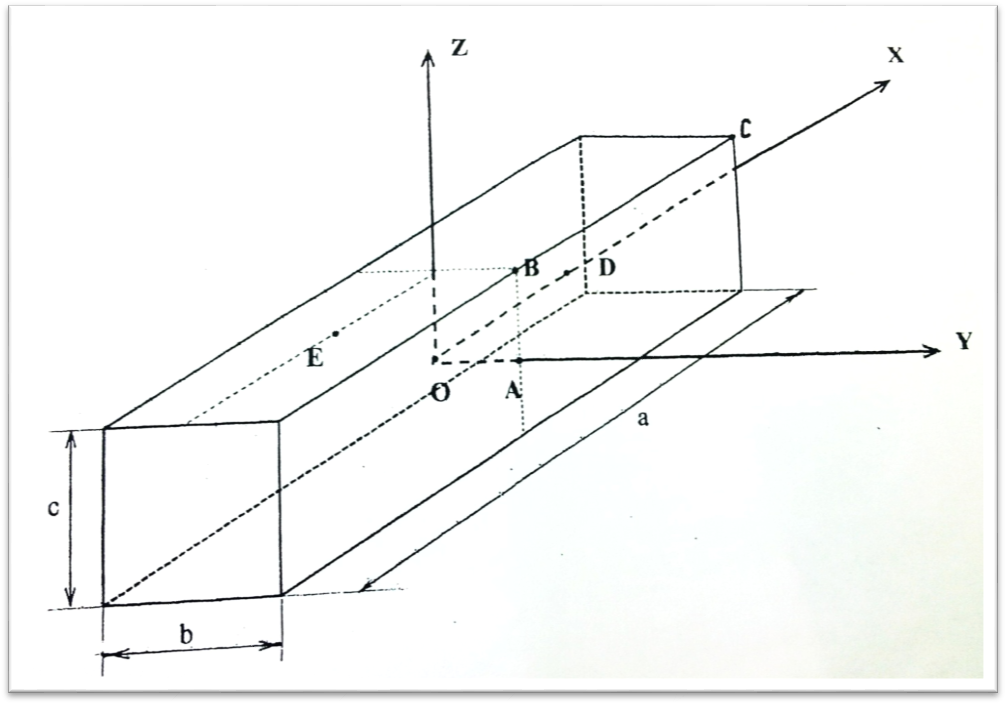
Исходные данные: материал углеродистая сталь

n =9

t=25 мин = 1500 сек

Т₀=1000+30n = 1270 ⁰C

a = 700+20n = 880 мм = 0,88 м

b = 200+30n = 470 мм = 0,47 м

с = 150 мм = 0,15 м

Т_НАЧ=20n = 180 ⁰C

α=150 Вт/(м²К)

а=1,5·10^-5 м²/с

λ = 18 Вт/(мК)

Найти: Т_О, Т_А, Т_В, Т_С, Т_D,

Решение:

По методу суперпозиции: если тело конечных размеров может быть представлено, как геометрическое место точек пересечения полубесконечных тел, и это тело нагревается при однородных (т.е. одинаковых со всех сторон) граничных условиях, то решение задачи для этого тела получается в результате перемножения решений для полубесконечных тел, пересечением которых оно является.

Ѳ_x,y,z=Ѳ_x·Ѳ_y·Ѳ_z

Характерные размеры , критерии Био и критерий Фурье для плоскостей:

δ_x= 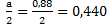м, Bi_x= 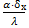= 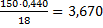, Fo_x=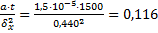

δ_y 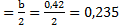м, Bi_y= 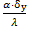= 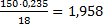, Fo_y=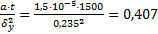

δ_z 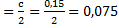м, Bi_z= 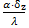= 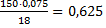, Fo_z=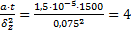

	μ₁²	μ₁	P	M	N
Bi_x	1,540	1,241	0,397	0,937	1,223
Bi_y	1,144	1,069	0,580	0,967	1,171
Bi_z	0,513	0,716	0,816	0,993	1,083

Нахождение Ѳ_x

Так как Fo_х≤ 0,3,то имеет место начальный период нагрева, в расчетах используем 2 слагаемых:

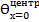=N(Bi_x)·exp(-μ₁²· Fo_x) + 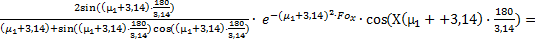1,223· exp(-1,54·0,116) + 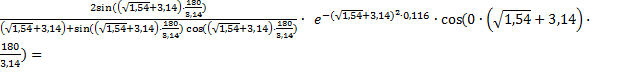1,059+ (-0,403)·0,1718·1=0,990

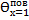=Р(Bi_x)·exp(-μ₁²· Fo_x) + 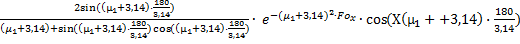= 0,397· exp(-1,54·0,116) + (-0,403)·0,1718·cos( 1 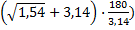=0,332+ 0,022=0,354

Х=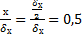

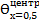=N(Bi_x)·cos(μ_{1 ·}X)·exp(-μ₁²· Fo_x) 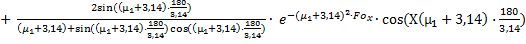= 1,223· cos( 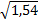·0,5·180/3,14)·exp(-1,54·0,116) + (-0,403)·0,1718·cos( 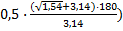=0,832+(-0,403)·0,1718·(-0,582)=0,872

Нахождение Ѳ_y

Так как Fo_y>0,3, то имеет место основной период нагрева и ограничиваемся одним слагаемым:

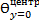=N(Bi_y)·exp(-μ₁²· Fo_y) 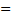1,171· exp(-1,144·0,407)=0,735

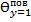=Р(Bi_y)·exp(-μ₁²· Fo_y) = 0,580· exp(-1,144·0,407 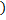=0,364

Нахождение Ѳ_z

Так как Fo_z>0,3, то имеет место основной период нагрева и ограничиваемся одним слагаемым:

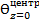=N(Bi_z)·exp(-μ₁²· Fo_z) = 1,083· exp(-0,513·4)=0,139

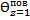=Р(Bi_z)·exp(-μ₁²· Fo_z) = 0,816· exp(-0,513·4)=0,105

Нахождение Ѳ в точках

Ѳ_O= 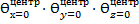=0,990·0,735·0,139=0,101

Ѳ_А= 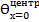· 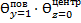=0,990·0,364·0,139=0,050

Ѳ_В= 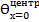· 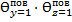=0,990·0,364·0,105=0,038

Ѳ_С= 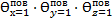=0,354·0,364·0,105=0,013

Ѳ_D= 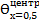· 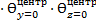=0,872·0,735·0,139=0,089

Температура в точках через 25 мин после посада заготовки в печь

При нагреве: Т=Т₀– Ѳ(Т₀-Т_нач)- температура в точках O,A,B,C,D через 25 минут после начала нагрева:

Т_О=Т₀– Ѳ_О(Т₀-Т_нач)=1270-0,101·(1270-180)=1160 ⁰C

Т_А=Т₀– Ѳ_А(Т₀-Т_нач)=1270-0,050·(1270-180)=1215 ⁰C

Т_В=Т₀– Ѳ_В(Т₀-Т_нач)=1270-0,038·(1270-180)=1228 ⁰C

Т_С=Т₀– Ѳ_С(Т₀-Т_нач)=1270-0,013·(1270-180)=1256 ⁰C

Т_D=Т₀– Ѳ_D(Т₀-Т_нач)=1270-0,089·(1270-180)=1173⁰C

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.