
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Построение эпюры материалов
Построение эпюры материалов
Продольная рабочая арматура в пролете 2Ø20 и 2Ø25 А500. Площадь этой арматуры Аs определена из расчета на действие максимального изгибающего момента в середине пролета. В целях экономии арматуры по мере уменьшения изгибающего момента к опорам два стержня обрываются в пролете, а два других доводятся до опор. Если продольная рабочая арматура разного диаметра, то до опор доводятся два стержня большего диаметра.
Определяем изгибающий момент, воспринимаемый сечением ригеля с полной запроектированной арматурой 2Ø20 и 2Ø25 А500 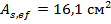 .
.
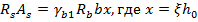
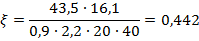
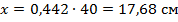
Изгибающий момент, воспринимаемый сечением ригеля, определяется из условия равновесия:
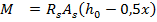
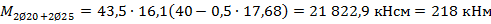
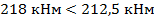 то есть больше действующего изгибающего момента от полной нагрузки, это значит, что прочность сечения обеспечена..
то есть больше действующего изгибающего момента от полной нагрузки, это значит, что прочность сечения обеспечена..
До опоры доводятся 2Ø25 А500С, h0 = 45 – 3 = 42 см , 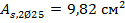 .
.
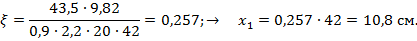
Определяем изгибающий момент, воспринимаемый сечением ригеля с рабочей арматурой в виде двух стержней, доводимых до опоры
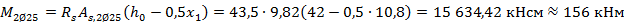
Откладываем в масштабе на эпюре моментов полученные значения изгибающих моментов М(2Ø20+2 Ø25) и М(2Ø25) и определяем место теоретического обрыва рабочей арматуры – это точки пересечения эпюры моментов с горизонтальной линией, соответствующей изгибающему моменту, воспринимаемому сечением ригеля с рабочей арматурой в виде двух стержней М(2Ø25) (рис.10)
Изгибающий момент в любом сечении ригеля определяется по формуле
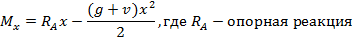
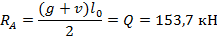
При 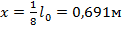
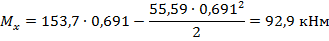
При 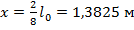

При 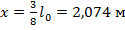
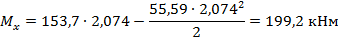
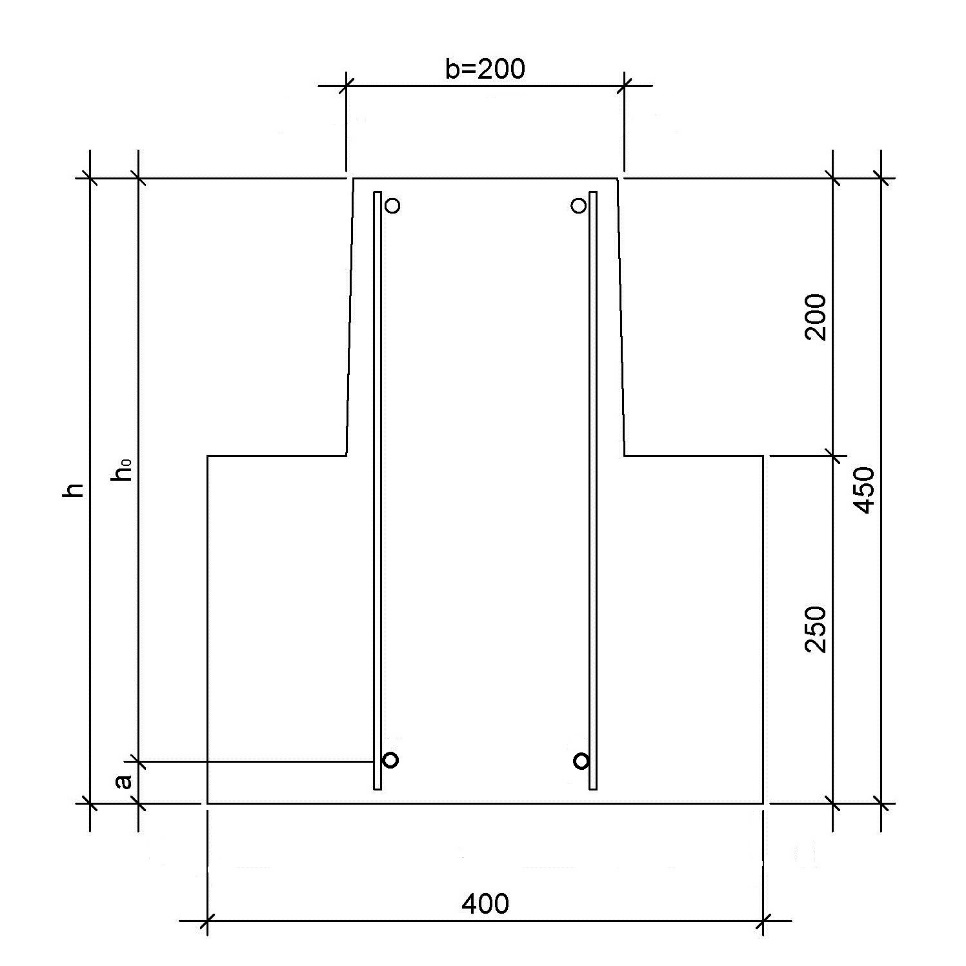
Рис. 9. Расчетное сечение ригеля в месте обрыва арматуры
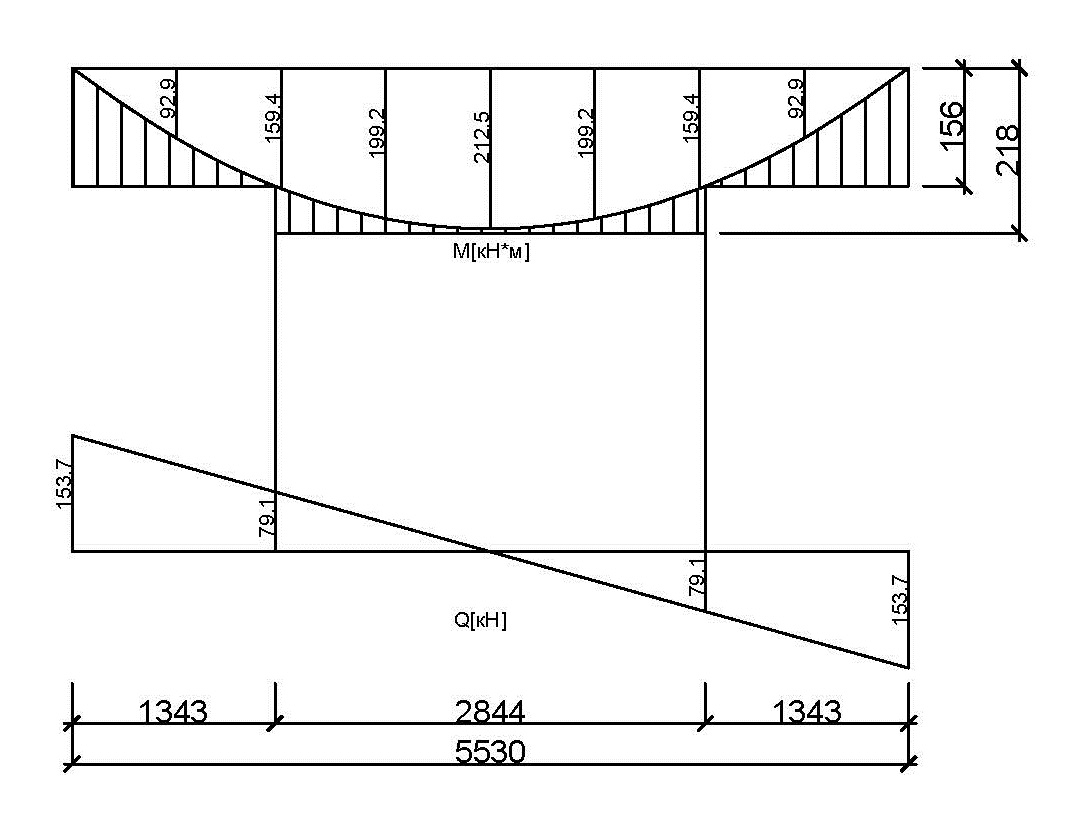
Рис. 10. Эпюра материалов в ригеле
Длина анкеровки обрываемых стержней определяется по следующей зависимости:
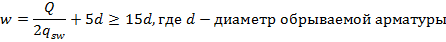
Поперечная сила Q определяется графически в месте теоретического обрыва, Q = 79,1 кН.
Поперечные стержни Ø8 А500 Rsw = 300 МПа с Аsw = 1,01 см2 в месте теоретического обрыва имеют шаг 10 см;
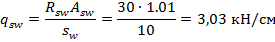
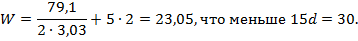
Принимаем W=30см
Место теоретического обрыва арматуры можно определить аналитически.
Для этого общее выражение для изгибающего момента нужно приравнять моменту, воспринимаемому сечением ригеля с арматурой 2Ø25 А500. 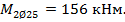
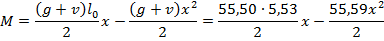
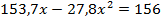
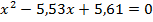
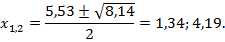
Это точки теоретического обрыва арматуры.
Длина обрываемого стержня будет равна: 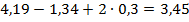 . Принимаем длину обрываемого стержня 3,5 м.
. Принимаем длину обрываемого стержня 3,5 м.
Определяем аналитически величину поперечной силы в месте теоретического обрыва арматуры при 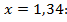
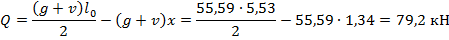
Это значение приблизительно совпадает с графически определенным 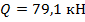 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|