Генерирование некоррелированной случайной последовательности с нормальным законом распределения.

Стр 1 из 2Следующая ⇒

Министерство по образованию РФ

РГРТУ

Кафедра РТС

Лабораторная работа №3

Генерирование коррелированных случайных процессов

Выполнили:

Ст. гр. 8112

Акаев И.Р

Нуркенов М.Ж

Проверил:

Гришаев Ю.Н.

Рязань 2011

Генерирование некоррелированной случайной последовательности с нормальным законом распределения.

Входной сигнал:

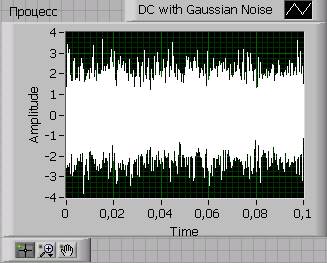
АКФ и энергетический спектр выходного сигнала:

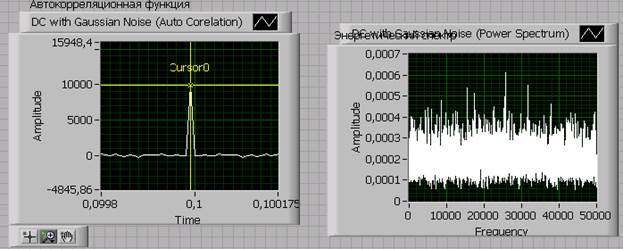
Наблюдаемый процесс является белым шумом, так как энергетический спектр на полосе частот от 0 до 50кГц равномерен, в силу того, что выходной процесс является некоррелированным. Верхняя частота спектра равна 50 кГц, так как она равна f_д/2,

f_д = 1/ Δt, а

Δt=0.000001

t, с	0,09999	0,1	0,10001	0,10002	0,10003
R_y(kΔt)	10131,5	-2,29	38,4161	45,3928	90,9452

Δt=0.000001

Случайный процесс является некоррелированным потому, что его корреляционная функция равна нулю для любого τ, отличного от нуля. Так, как при моделировании всегда используется реализация случайного процесса конечной длины, в измеренной корреляционной функции имеются нескомпенсированные остатки.

Исследование СС-фильтра.

k=5

bi=1/k^1/2=1/5^1/2=0,448

t, с
R_y(kΔt)	9924,73	7936,27	5999,45	4111,43	2181,48	247,103

АКФ и энергетический спектр:

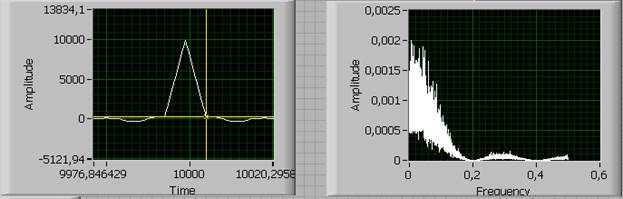
R_y(0) = (b₀² + b₁² + b₂² + … + b_k²)σ_x²= σ_x²5b_k²= σ_x²5*0.448²= 1.00352σ_x²

R_y(Δt) = (b₀b₁ + b₁b₂ + b₂b₃+ b₃b₄)σ_x²= σ_x²4b_k²= σ_x²4*0.448²= 0.803σ_x²

R_y(2Δt) = (b₀b₂ + b₁b₃ + b₂b₄)σ_x²= σ_x²3b_k²= σ_x²3*0.448²= 0.6021σ_x²

R_y(3Δt) = (b₀b₃ + b₁b₄)σ_x²= σ_x²2b_k²= σ_x²2*0.448²= 0.4σ_x²

R_y(4Δt) = b₀b_kσ_x² =σ_x²b_k²= 0.2007σ_x²

R_y(kΔt + Δt) = 0

КИХ-фильтр со всеми положительными коэффициентами эквивалентен ФНЧ.

При положительных коэффициентах корреляционная функция тоже будет монотонно спадающей за исключением нескомпенсированных остатков.

У половины коэффициентов (b₂b₄ ) изменим знак коэффициентов на обратный^.

АКФ и энергетический спектр:

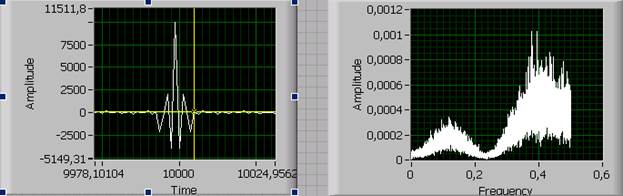
R_y(0) = (b₀² + b₁² + b₂² + … + b_k²)σ_x²= σ_x²5b_k²= σ_x²5*0.448²= 1.00352σ_x²

R_y(Δt) = (b₀b₁ + b₁b₂ + b₂b₃+ b₃b₄)σ_x²= σ_x²3b_k²= -(σ_x²3*0.448²)=- 0.803σ_x²

R_y(2Δt) = (b₀b₂ + b₁b₃ + b₂b₄)σ_x²= σ_x²2b_k²= σ_x²2*0.448²= 0.6021σ_x²

R_y(3Δt) = (b₀b₃ + b₁b₄)σ_x²= σ_x²b_k²= σ_x²0.448²= 0.448σ_x²

R_y(4Δt) = b₀b_kσ_x² =σ_x²b_k²= 0.2007σ_x²

R_y(kΔt + Δt) = 0

t, с
R_y(kΔt)	9988,78

Изменяя знак коэффициентов на обратный можно добиться того, что КИХ-фильтр становится эквивалентен ФВЧ.

При отрицательных коэффициентах импульсная характеристика становится колебательной, и корреляционная функция будет колебательной затухающей.

12 Следующая ⇒