Контакты

Случайная статья

Иррациональные уравнения. Глоссарий по теме. Теоретический материал для самостоятельного изучения

Стр 1 из 2Следующая ⇒

Иррациональные уравнения

Рекомендую видео урок по ссылке

https://resh.edu.ru/subject/lesson/5569/main/159267/

Глоссарий по теме

Иррациональное уравнение– это уравнения, в которых неизвестное находится под знаком корня.

Свойство: при возведении обеих частей уравнения в натуральную степень получается уравнение – следствие данного.

Теоретический материал для самостоятельного изучения

Иррациональное уравнение– это уравнения, в которых неизвестное находится под знаком корня.

Свойство: при возведении обеих частей уравнения в натуральную степень получается уравнение – следствие данного.

Рассмотрим виды иррациональных уравнений

В этом случае мы можем воспользоваться определением квадратного корня.

Из него следует, что а≥0, тогда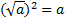

Для нашего случая получим

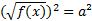или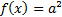

2.

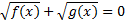
Мы знаем, что сумма положительных чисел равна нулю тогда и только тогда, когда каждое из слагаемых равно нулю.
Т.е.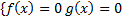

3.

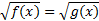
По определению квадратного корня f(x) > 0. Таким образом, чтобы найти такие значения неизвестной, при которых выполняются следующие условия:

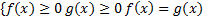
Примеры:

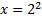
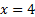
Ответ: х=4

2.

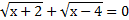
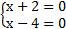
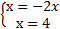
следовательно, решений нет

Ответ: решений нет

3. Решить уравнение: 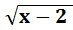= 6

Решение. 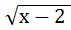= 6, возведём обе части уравнения в квадрат (чтобы «избавиться» от квадратного корня);

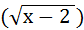² = 6²;

x – 2 = 36;

x = 36 +2;

x = 38.

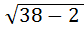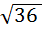Проверка при x = 38. = 6;

= 6;

6 = 6 (верно).

Ответ: 38.

Решить самостоятельно ( по образцу примера 3)

1). = 5

2). = 9

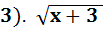- 4 = 0

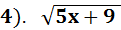- 7= 0

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.