ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ. по линейной алгебре. Инд. задание 1.. Инд. задание 2.. Инд. задание 3.. Инд. задание 4.

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

по линейной алгебре

Условия для индивидуальных заданий – в учебном пособии «Учебные и контрольные задания по математике. Высшая алгебра» - СПб.: ОЦЭиМ.

Каждому студенту сопоставляется его порядковый номер в списке группы; обозначим его Х (число Х будет определять номер вашей индивидуальной задачи).

Инд. задание 1.

Решить систему методом Гаусса и сделать проверку.

Система берется из контрольного задания №3 (с.24 – 34), № Хb).

Например, если Х=13 (то есть порядковый номер студента -13), то надо решать систему №13 п. b) на с. 28.

Инд. задание 2.

Проверить наличие линейной зависимости для данного набора векторов и, если набор линейно зависимый, выписать выражение линейной зависимости.

Набор векторов берется из контрольного задания №6 (с. 78-83), №Ха), причем параметр 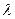, присутствующий в наборе векторов, определяется следующим образом:

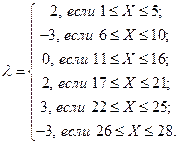
Например, если ваш номер Х=23, то в набор векторов под номером 23а) на с. 80 вы подставляете 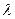=3 и для полученного набора (1,1,1,2), (3,0,1,2), (-2,3,0,0) выполняете задание.

Инд. задание 3.

Выполнить контрольное задание №1 (с. 8 – 16) для №Х а), b), с).

Инд. задание 4.

Вычислить определитель двумя любыми способами.

Определитель берется из контрольного задания №2 (с. 18- -21), №Ха).

Инд. задание 5.

Решить систему методом Крамера. (Если определитель системы равен нулю, решить систему методом Гаусса.)

Система – берется из контрольного задания №3 (с. 24 – 34), №Ха).

Инд. задание 6.

Для данной матрицы найти обратную матрицу и сделать проверку.

Матрица берется из контрольного задания №2 (с. 18-21), №Хb).