
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 1. Задание 2. Задание 3. Задание 4. Задание 5. Задание 6. Задание 7. Задание 8. Задание 10. Задание 11. Заключение
Задание 1
Доказать или опровергнуть всеми известными вам методами для произвольных множеств справедливость следующих утверждений (при доказательстве указывать используемые определения, правила, законы и эквивалентные преобразования):
1.1) 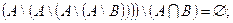
1.2) 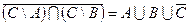 ;
;
Теоретическая часть:
Множество – совокупность некоторых вполне различимых элементов, объединенных каким либо свойством и мыслимых как единое целое.
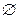 - пустое множество, множество, не содержащее ни одного элемента.
- пустое множество, множество, не содержащее ни одного элемента.
Множества равны, если они состоят из одних и тех же элементов.
Два множества не равны, если в одном из множеств есть элемент, не принадлежащий другому множеству.
X подмножество Y, если 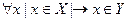 ;
;
X и Y равны 
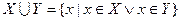
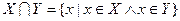
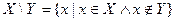
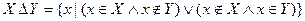
Множество, которое содержит все элементы, из которых состоит множество X, называется универсумом.
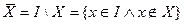
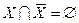 ;
;  ;
; 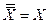 ;
; 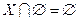 ;
; 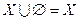
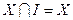 ;
; 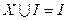
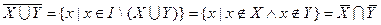
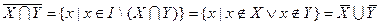
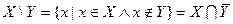
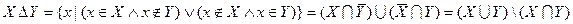
Множество всех подмножеств I и операции 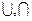 и
и 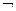 образуют алгебру подмножеств множества I.
образуют алгебру подмножеств множества I.
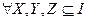 выполняется:
выполняется:
Идемпотентность: 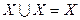 ;
; 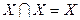
Коммутативность: 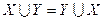 ;
; 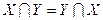
Ассоциативность: 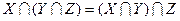 ;
; 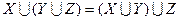
Дистрибутивность: 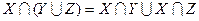 ;
; 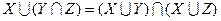
Поглощение: 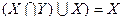
При доказательствах были использованы законы алгебры логики для простых и составных высказываний:
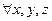 - логические утверждения, тогда:
- логические утверждения, тогда:
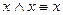 ;
; 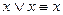 - идемпотентность
- идемпотентность
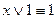 ;
; 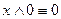
 ;
; 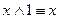
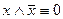 - закон противоречия
- закон противоречия
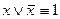 - закон исключения третьего
- закон исключения третьего
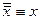 - закон двойного отрицания
- закон двойного отрицания
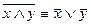 ;
; 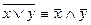 - законы де Моргана
- законы де Моргана
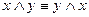 ;
; 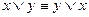 - коммутативность
- коммутативность
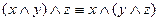 ;
; 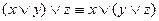 - ассоциативность
- ассоциативность
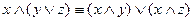 ;
; 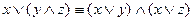 - дистрибутивность
- дистрибутивность
Практическая часть:
Доказательство 1.1:
1.1.1)Доказательство с помощью метода от противного:
Предположим, что:
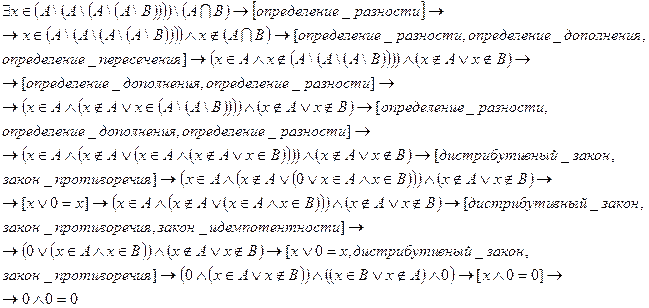
Следовательно, наше предположение неверно. Т. о. равенство 1.1 выполняется.
1.1.2)Доказательство с помощью эквивалентных преобразований:
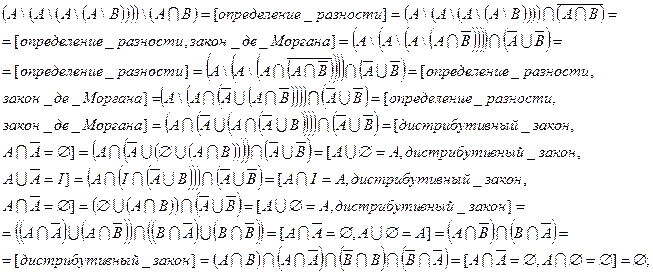
Т. о. равенство 1.1 выполняется.
1.1.3)Доказательство с помощью диаграмм Эйлера-Вена:
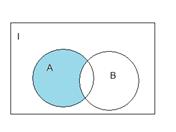
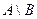
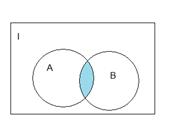
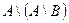
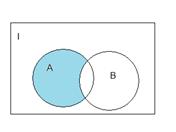
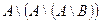
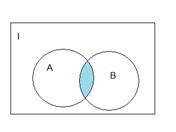
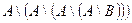

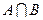
Разность между одинаковыми диаграммами дает пустое множество.
Т. о. равенство 1.1 выполняется.
Доказательство 1.2:
1.2.1) Доказательство взаимным включением:
1) Докажем, что: 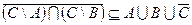
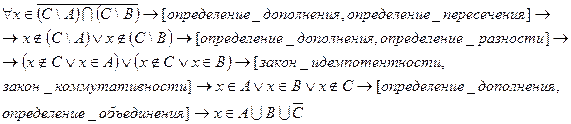
ч.т.д.
2) Докажем, что: 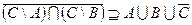
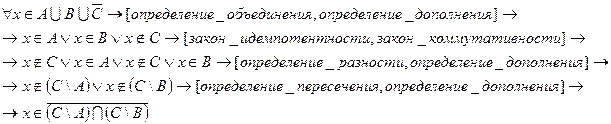
ч.т.д.
Т. о. равенство 1.2 выполняется.
1.2.2) Доказательство с помощью метода от противного:
1) Докажем, что: 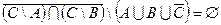 ;(*)
;(*)
Предположим, что:
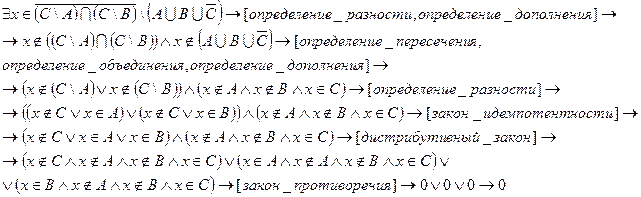
Следовательно, наше предположение неверно. Т. о. равенство (*) выполняется.
2) Докажем, что: 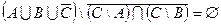 ; (**)
; (**)
Предположим, что:
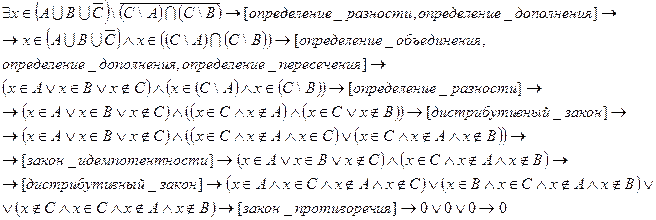
Следовательно, наше предположение неверно. Т. о. равенство (**) выполняется.
Т. о. равенство 1.2 выполняется.
1.2.3)Доказательство с помощью диаграмм Эйлера-Вена:
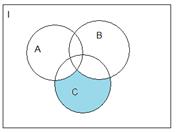
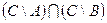
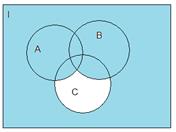
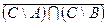
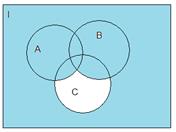
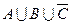
Т. о. равенство 1.1 выполняется.
1.2.4)Доказательство с помощью эквивалентных преобразований:
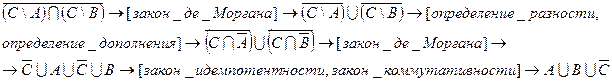
Т. о. равенство 1.2 выполняется.
Задание 2
Доказать для произвольных множеств X,Y,W,Z справедливость (или несправедливость) следующих высказываний:
2.1) 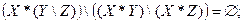
2.2) 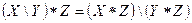 ;
;
Теоретическая часть:
Множество – совокупность некоторых вполне различимых элементов, объединенных каким либо свойством и мыслимых как единое целое.
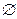 - пустое множество, множество, не содержащее ни одного элемента.
- пустое множество, множество, не содержащее ни одного элемента.
Множества равны, если они состоят из одних и тех же элементов.
Два множества не равны, если в одном из множеств есть элемент, не принадлежащий другому множеству.
X подмножество Y, если 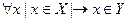 ;
;
X и Y равны 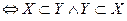
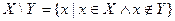
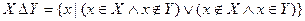
Множество, которое содержит все элементы, из которых состоит множество X, называется универсумом.
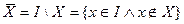
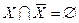 ;
; 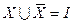 ;
; 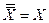 ;
; 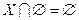 ;
; 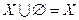
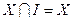 ;
; 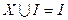
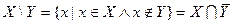
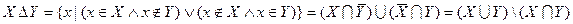
При доказательствах были использованы законы алгебры логики для простых и составных высказываний:
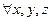 - логические утверждения, тогда:
- логические утверждения, тогда:
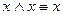 ;
; 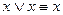 - идемпотентность
- идемпотентность
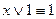 ;
; 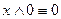
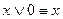 ;
; 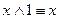
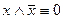 - закон противоречия
- закон противоречия
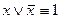 - закон исключения третьего
- закон исключения третьего
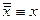 - закон двойного отрицания
- закон двойного отрицания
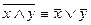 ;
; 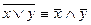 - законы де Моргана
- законы де Моргана
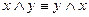 ;
; 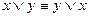 - коммутативность
- коммутативность
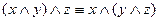 ;
; 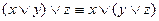 - ассоциативность
- ассоциативность
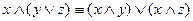 ;
;  - дистрибутивность
- дистрибутивность
Кортеж (упорядоченное множество) – совокупность элементов, в которой каждый элемент занимает вполне определенное место.
Прямым (декартовым) произведением множества X на множество Y – называется упорядоченное множество A, состоящее из таких и только таких элементов (x,y), что x принадлежит X, а y принадлежит Y.
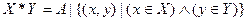 ;
;
Операция декартовое произведение не коммутативна.
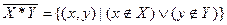
Практическая часть:
Доказательство 2.1:
2.1) Доказательство с помощью метода от противного:
Предположим, что:
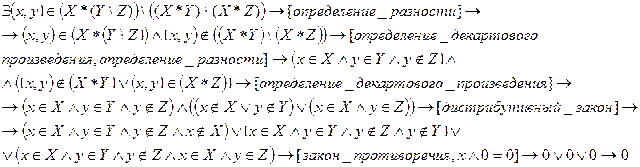
Следовательно, наше предположение неверно. Т. о. равенство 2.1 выполняется.
Доказательство 2.2:
2.2)Доказательство взаимным включением:
1) Докажем, что: 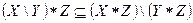 ; (*)
; (*)
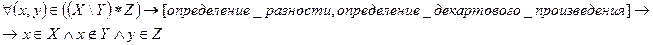
Дальнейшие рассуждения не возможны. Следовательно, (*) неверно.
2) Докажем, что: 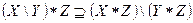
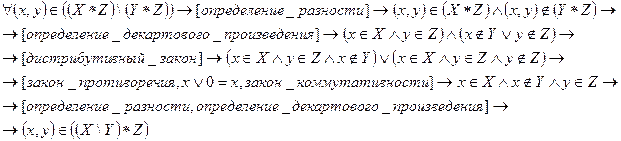
ч.т.д.
Т. о. равенство 1.2 не выполняется, но примет вид 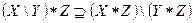 .
.
Задание 3
Доказать или опровергнуть, что для множеств А,В,С, где 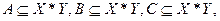 причем
причем 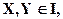 справедливы высказывания:
справедливы высказывания:
3.1) 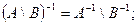
3.2) 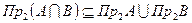 ;
;
Теоретическая часть:
Множество – совокупность некоторых вполне различимых элементов, объединенных каким либо свойством и мыслимых как единое целое.
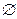 - пустое множество, множество, не содержащее ни одного элемента.
- пустое множество, множество, не содержащее ни одного элемента.
Множества равны, если они состоят из одних и тех же элементов.
Два множества не равны, если в одном из множеств есть элемент, не принадлежащий другому множеству.
X подмножество Y, если 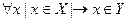 ;
;
X и Y равны 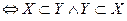
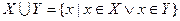
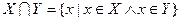
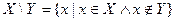
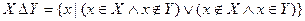
Множество, которое содержит все элементы, из которых состоит множество X, называется универсумом.
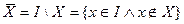
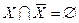 ;
; 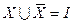 ;
; 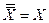 ;
; 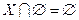 ;
; 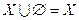
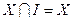 ;
; 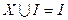
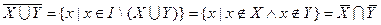
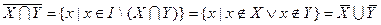
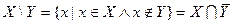
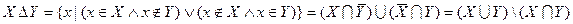
Множество всех подмножеств I и операции 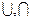 и
и 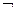 образуют алгебру подмножеств множества I.
образуют алгебру подмножеств множества I.
 выполняется:
выполняется:
Идемпотентность: 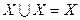 ;
; 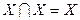
Коммутативность: 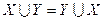 ;
; 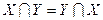
Ассоциативность: 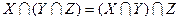 ;
; 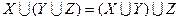
Дистрибутивность: 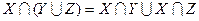 ;
; 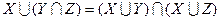
Поглощение: 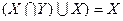
При доказательствах были использованы законы алгебры логики для простых и составных высказываний:
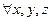 - логические утверждения, тогда:
- логические утверждения, тогда:
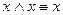 ;
; 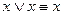 - идемпотентность
- идемпотентность
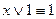 ;
; 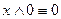
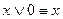 ;
; 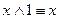
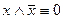 - закон противоречия
- закон противоречия
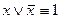 - закон исключения третьего
- закон исключения третьего
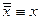 - закон двойного отрицания
- закон двойного отрицания
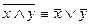 ;
; 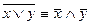 - законы де Моргана
- законы де Моргана
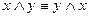 ;
; 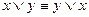 - коммутативность
- коммутативность
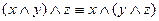 ;
; 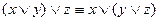 - ассоциативность
- ассоциативность
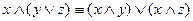 ;
;  - дистрибутивность
- дистрибутивность
Кортеж (упорядоченное множество) – совокупность элементов, в которой каждый элемент занимает вполне определенное место.
Прямым (декартовым) произведением множества X на множество Y – называется упорядоченное множество A, состоящее из таких и только таких элементов (x,y), что x принадлежит X, а y принадлежит Y.
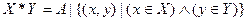 ;
;
Операция декартовое произведение не коммутативна.
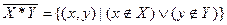
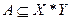 ;
; 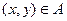
Операция проектирования справедлива для множеств, элементами которых являются кортежи одинаковой длины.
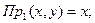
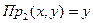
Операция проектирования множества, состоящего из кортежей - операция выделения первых, вторых и т. д. компонент кортежей и образование из них нового множества.
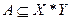 ;
; 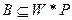
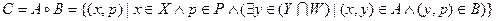
Композиция применима к упорядоченным множествам, состоящим из двоек.
y – компонирующий элемент.
Пусть 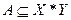 ;
; 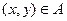 .
.
Инверсией кортежа 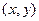 называется и через
называется и через 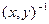 обозначается кортеж
обозначается кортеж 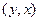 , где
, где  , а
, а 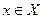 .
.
Инверсия произвольного множества состоит из его пар и обозначается 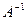 . Следовательно, для любого произвольного кортежа
. Следовательно, для любого произвольного кортежа 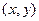 справедливы высказывания:
справедливы высказывания:
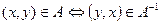 ;
;
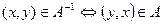 ;
;
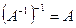 .
.
Практическая часть:
Доказательство 3.1:
3.1)Доказательство взаимным включением:
1) Докажем, что: 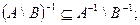
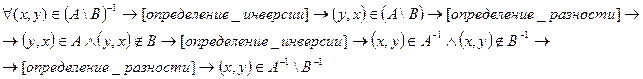 ч.т.д.
ч.т.д.
2) Докажем, что: 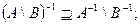
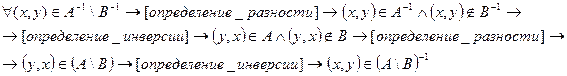
ч.т.д.
Т. о. равенство 3.1 выполняется.
Доказательство 3.2:
3.2)Доказательство взаимным включением:
1) Докажем, что: 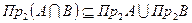
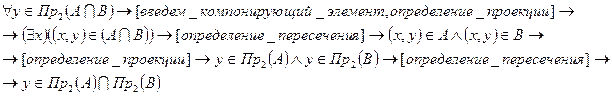
Т.к. пересечение 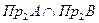 включено в объединение
включено в объединение 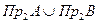 , то
, то 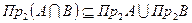 выполняется.
выполняется.
2) Докажем, что: 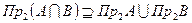
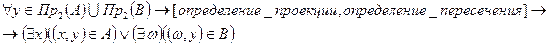
Дальнейшие рассуждения не имеют смысла, так как в выражении 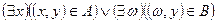 2 разных компонирующих элемента, следовательно данное выражение не возможно представить в ином виде. Обратное включение не выполняется.
2 разных компонирующих элемента, следовательно данное выражение не возможно представить в ином виде. Обратное включение не выполняется.
Т. о. утверждение 3.2 верно.
Задание 4
Доказать, что если 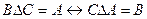 .
.
Теоретическая часть:
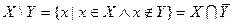
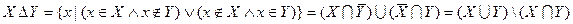
На диаграммах Эйлера-Вена множества могут находиться в различных взаимных положениях: общее, не пересекаться, равные, и каждое множество может быть включено в другое.
Практическая часть:
Проведем доказательство с помощью диаграмм Эйлера-Вена. Для этого рассмотрим 5 случаев взаимного положения 2-х множеств: общее, не пересекаются, равны, одно включено в другое и наоборот.
1)Общее: 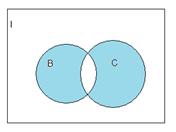
Пространство, выделенное на картинке, есть множество А. Тогда , рассматривая симметрическую разность между множеством А и множеством С, получим множество В, т.к. разность между А и С даст не закрашенный кусочек, а разность между С и А, исключит элементы, принадлежащие множеству С.
2)Не пересекаются:
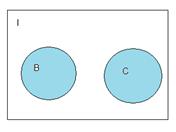
Пространство, выделенное на картинке, есть множество А. Тогда, рассматривая симметрическую разность между множеством А и множеством С, получим множество В, т.к. разность между А и С даст пустое множество, а разность между С и А, исключит элементы, принадлежащие множеству С.
3) Равны:
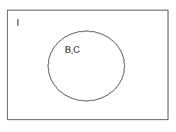 Т.к. множества равны, то их симметрическая разность даст множество А, которое будет пустом. Симметрическая разность множества А с множеством С, даст нам множество В. Следовательно, утверждение также верно.
Т.к. множества равны, то их симметрическая разность даст множество А, которое будет пустом. Симметрическая разность множества А с множеством С, даст нам множество В. Следовательно, утверждение также верно.
4) 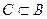 :
:
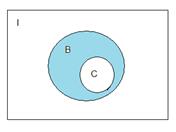 Пространство, выделенное на картинке, есть множество А. Тогда, рассматривая симметрическую разность между множеством А и множеством С, получим множество В, т.к. разность между А и С даст не закрашенный кусочек, а разность между С и А, оставит закрашенную область.
Пространство, выделенное на картинке, есть множество А. Тогда, рассматривая симметрическую разность между множеством А и множеством С, получим множество В, т.к. разность между А и С даст не закрашенный кусочек, а разность между С и А, оставит закрашенную область.
5) 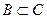 :
:
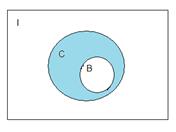 Пространство, выделенное на картинке, есть множество А. Тогда, рассматривая симметрическую разность между множеством А и множеством С, получим множество В, т.к. разность между А и С даст не закрашенный кусочек, а разность между С и А, оставит закрашенную область.
Пространство, выделенное на картинке, есть множество А. Тогда, рассматривая симметрическую разность между множеством А и множеством С, получим множество В, т.к. разность между А и С даст не закрашенный кусочек, а разность между С и А, оставит закрашенную область.
Т.к. во всех случаях данные соотношения остаются верными, то от сюда следует, что 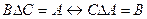 .
.
Задание 5
Построить отношение:
1) Не рефлексивное, симметричное, транзитивное;
2) Антирефлексивное, несимметричное, нетранзитивное.
Теоретическая часть:
Множество – совокупность некоторых вполне различимых элементов, объединенных каким либо свойством и мыслимых как единое целое.
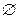 - пустое множество, множество, не содержащее ни одного элемента.
- пустое множество, множество, не содержащее ни одного элемента.
Множества равны, если они состоят из одних и тех же элементов.
Два множества не равны, если в одном из множеств есть элемент, не принадлежащий другому множеству.
X подмножество Y, если 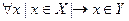 ;
;
X и Y равны 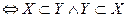
Кортеж (упорядоченное множество) – совокупность элементов, в которой каждый элемент занимает вполне определенное место.
Прямым (декартовым) произведением множества X на множество Y – называется упорядоченное множество A, состоящее из таких и только таких элементов (x,y), что x принадлежит X, а y принадлежит Y.
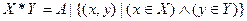 ;
;
Операция декартовое произведение не коммутативна.
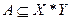 ;
; 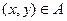
Операция проектирования справедлива для множеств, элементами которых являются кортежи одинаковой длины.
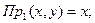
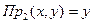
Операция проектирования множества, состоящего из кортежей - операция выделения первых, вторых и т. д. компонент кортежей и образование из них нового множества.
Отношением 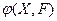 на произвольном множестве
на произвольном множестве 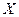 называется пара
называется пара 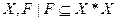 .
.
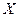 - область задания,
- область задания, 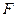 - график.
- график.
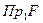 - область определения.
- область определения.
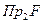 - область значений.
- область значений.
Способы задания отношений:
1) теоретический
2) матричный (с помощью матрицы смежности)
3) графический
Отношение 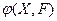 :
:
- рефлексивное, если: 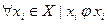 , единицы на главной диагонали матрицы смежности;
, единицы на главной диагонали матрицы смежности;
-антирефлексивное, если: 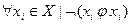 ,нули на главной диагонали матрицы смежности;
,нули на главной диагонали матрицы смежности;
-симметричное, если: 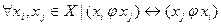 ,единицы симметричны главной диагонали матрицы смежности;
,единицы симметричны главной диагонали матрицы смежности;
- несимметричное, если: 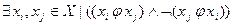 ;
;
- антисимметричное, если: 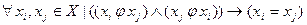 ,нет ни одной симметричной пары единиц относительно главной диагонали матрицы смежности и на главной диагонали матрицы смежности единицы;
,нет ни одной симметричной пары единиц относительно главной диагонали матрицы смежности и на главной диагонали матрицы смежности единицы;
- транзитивное, если: 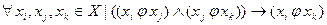 , множество элементов принадлежащих композиции матрицы смежности самой на себя будет подмножеством множества элементов исходной матрицы смежности ;
, множество элементов принадлежащих композиции матрицы смежности самой на себя будет подмножеством множества элементов исходной матрицы смежности ;
- нетранзитивное, если транзитивность не выполняется для всех или для некоторых 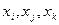 ;
;
- связное, если 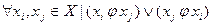
Практическая часть:
1) Не рефлексивное, симметричное, транзитивное;
1.1)матричный способ задания:
1.2) теоретический способ задания:
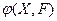 ,
, 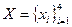 ,
, 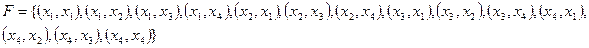
1.3)графический способ задания:






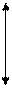
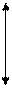
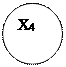
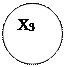
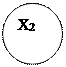
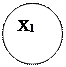
2) Антирефлексивное, несимметричное, нетранзитивное;
1.1)матричный способ задания:
1.2) теоретический способ задания:
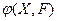 ,
, 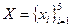 ,
, 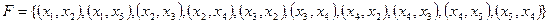
1.3)графический способ задания:

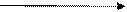







Задание 6
Пусть R1 и R2 отношения, заданные на множестве X. Приведите доказательство:
Доказать, что если отношения R1 и R2 симметричны, то симметрично отношение R1\ R2.
Теоретическая часть:
Отношением 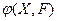 на произвольном множестве
на произвольном множестве 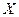 называется пара
называется пара 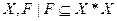 .
.
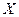 - область задания,
- область задания, 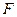 - график.
- график.
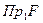 - область определения.
- область определения.
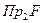 - область значений.
- область значений.
Отношение 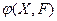 :
:
-симметричное, если: 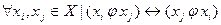 ,единицы симметричны главной диагонали матрицы смежности;
,единицы симметричны главной диагонали матрицы смежности;
- несимметричное, если: 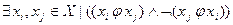 ;
;
- антисимметричное, если: 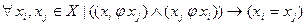 ,нет ни одной симметричной пары единиц относительно главной диагонали матрицы смежности и на главной диагонали матрицы смежности единицы;
,нет ни одной симметричной пары единиц относительно главной диагонали матрицы смежности и на главной диагонали матрицы смежности единицы;
Пусть имеем 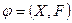 и
и 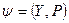 , тогда
, тогда
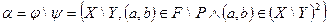
Практическая часть:
Пусть R1ÌA´A и
R2ÌA´A
Т.к. R1 и R2 симметричны, то
"(a,b)ÎA´A aR1b→ bR1a, "(c,d)Î A´A cR2d→ dR2c
"(a,b), (c,d)Î A´A aR1b\ cR2d→ bR1a\ dR2c
пусть R1\R2=R Þ"(a,b), (c,d)Î A´A aR1b\ cR2d→ bR1a\ dR2c Þ
"(e,f)Î A´A eRf→ fRe Þ R1\R2 –симметрично. Ч.т.д.
Задание 7
Задайте морфизмы между отношениями, являющиеся:
1) Эпиморфизмом;
2) Изоморфизмом;
Теоретическая часть:
Морфизм – перенесение свойств одного объекта на другой.
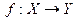
В дискретной математике под функцией подразумевается отображение некоторого множества 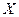 на
на 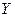 .
.
Функцией называется функциональное соответствие: 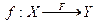
Область определения: 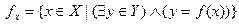
Область значений: 
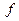 - тотальная, если:
- тотальная, если: 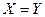
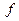 - инъективная, если:
- инъективная, если: 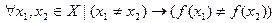
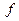 - всюду определенная, если:
- всюду определенная, если: 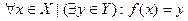
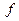 - сюръективная, если:
- сюръективная, если: 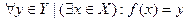
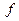 - биективная, если она тотальная, инъективная, всюду определенная и сюръективная.
- биективная, если она тотальная, инъективная, всюду определенная и сюръективная.
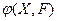 и
и 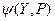 - некоторые отношения, тогда:
- некоторые отношения, тогда:
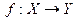
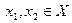 ;
; 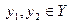
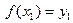 ;
; 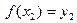
Если 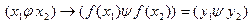 , то данный морфизм – гомоморфизм между отношениями.
, то данный морфизм – гомоморфизм между отношениями.
Если гомоморфизм – инъективен, то он – мономорфизм.
Если гомоморфизм – сюръективен, то он – эпиморфизм.
Если гомоморфизм – биективен, то он – изоморфизм.
Практическая часть:
 1)
1)
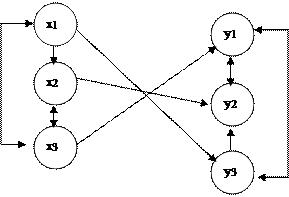 |
Свойства: функциональность, не всюду определенность, инъективность, сюръективность.
2)






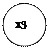




Свойства: функциональность, всюду определенность, инъективность, сюръективность.
Задание 8
Заданы нечеткие множества 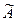 и
и 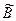 , где:
, где:
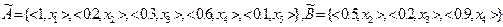 , на четком множестве
, на четком множестве 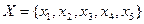 . Найти нечеткое множество
. Найти нечеткое множество 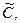 такое что:
такое что:
8.1) 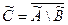 ;
;
8.2) 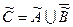 ;
;
а также степень нечеткости множеств 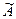 и
и 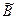 .
.
Теоретическая часть:
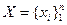
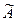 - нечеткое множество:
- нечеткое множество:
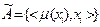 , где
, где 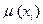 - значение функция принадлежности
- значение функция принадлежности 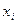 к нечеткому множеству.
к нечеткому множеству.
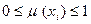
Элементы 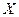 , для которых степень принадлежности к
, для которых степень принадлежности к 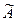 больше нуля – подмножество элементов
больше нуля – подмножество элементов 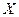 - носитель
- носитель 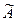 .
.
Логика Заде:
Нечеткое высказывание 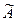 - предложение или предположение, на основании которого можно судить о степени истинности его в настоящее время.
- предложение или предположение, на основании которого можно судить о степени истинности его в настоящее время.
0 – ложное, 1 – истинное, 0.5 – индифферентно.
Операции нечеткой логики:
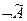 - высказывание, степень истинности которого:
- высказывание, степень истинности которого: 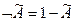 ;
;
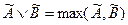 ;
;
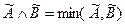 ;
;
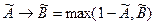 ;
;
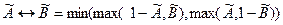 ;
;
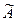 ,
, 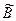 - нечеткие множества, тогда:
- нечеткие множества, тогда:
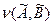 - степень включения
- степень включения 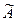 в
в 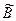 :
:
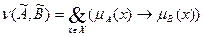
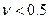 -
- 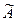 нечетко не включается в
нечетко не включается в 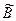 .
.
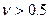 -
- 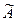 нечетко включается в
нечетко включается в 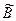 .
.
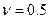 -
- 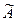 и
и 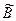 нечетко равны.
нечетко равны.
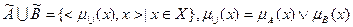 ;
;
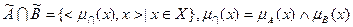 ;
;
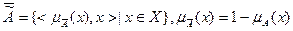 ;
;
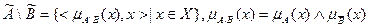 ;
;
Степень нечеткости – отрицание степени равенства 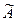 и его носителя.
и его носителя.
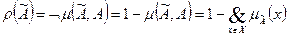
Практическая часть:
8.1)
Для определения значения функции принадлежности использовались определения дополнения и разности нечетких множеств.
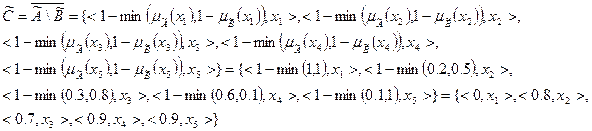
8.2)
Для определения значения функции принадлежности использовались определения дополнения и объединения нечетких множеств.
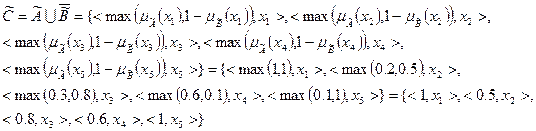
Степень нечеткости:
1)
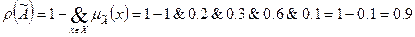
2)
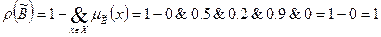
Задание 10
Построить логическую схему на четыре входа 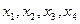 и один выход yв базисе НЕ – ИЛИ, причем выход y равен 0 тогда и только тогда, когда два или менее из ее входов равны 0.
и один выход yв базисе НЕ – ИЛИ, причем выход y равен 0 тогда и только тогда, когда два или менее из ее входов равны 0.
Теоретическая часть:
Были использованы законы алгебры логики для простых и составных высказываний:
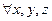 - логические утверждения, тогда:
- логические утверждения, тогда:
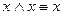 ;
; 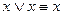 - идемпотентность
- идемпотентность