
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие №45. Пример
Практическое занятие №45
Тема: Исследование функции с помощью производной.
Сведения из теории:
Общая схема построения графиков функций:
1) найти область определения функции;
2) найти точки пересечения графика функции с осями координат;
3) найти промежутки монотонности функции и экстремумы функции;
4) построить график функции, используя полученные результаты исследования.
Пример
Исследовать функцию 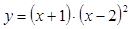 и построить ее график.
и построить ее график.
Решение:
1) Данная функция является многочленом (можно раскрыть скобки, получим многочлен третьей степени), поэтому она определена, непрерывна и дифференцируема при любых х. Поэтому область определения функции – вся числовая прямая.
Д(у): хÎ(-∞;+∞)
2) Вычислим точки пересечения графика функции с осями координат: график функции у=(х+1)·(х–2)2 пересекает ось Ох при у=0 (надо функцию приравнять к 0 и решить полученное уравнение), т. е.
(х+1)·(х–2)2=0;
х+1=0 или (х–2)2=0;
х=-1 или х=2.
График функции у=(х+1)·(х–2)2 пересекает ось Оу при х=0 (надо в функцию вместо х подставить 0 и посчитать), т. е.
у=(0+1)·(0–2)2=1·4=4.
Т.о. мы получили три точки: (–1; 0), (2; 0), (0; 4).
3) Найдем промежутки монотонности функции и ее экстремумы с помощью производной:
у’= ((х+1)·(х–2)2)’=((х+1)·(х2-4х+4)’=((х3-4 х2+4х+ х2 -4х+4)’=( х3 -3 х2 +4)’=
3 х2 -6х = 3х·(х–2).
Из уравнения у¢=0 найдем критические точки:
3х·(х–2)=0;
х1=0, х2=2.
Результаты решения занесем в таблицу:
| х | (–∞, 0) | (0; 2) | (2; +∞) | ||
| у¢ | + | – | + | ||
| у | 
| 
| 
| ||
| возрастает | max | убывает | min | возрастает |
Функция возрастает на интервалах (–∞, 0) и (2, +∞), убывает на интервале
(0; 2), имеет максимум при х=0 и минимум при х=2: уmax=у(0)=4; уmin=у(2)=0.
5) По полученным точкам строим график:
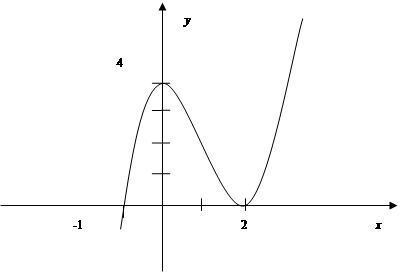
Рисунок 1. График функции у=(х+1)·(х–2)2
Задания для самостоятельного решения:
Исследуйте следующие функции и постройте их графики:
1. 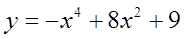
2. 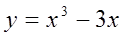
3. 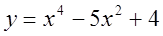
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|