Запишите тему урока. Далее изучите теоретический материал, а то, что выделено курсивом – запишите в тетрадях. Рисунок 1 постройте в тетрадях.

Тема. Построение сечений пирамиды. Достраивание тетраэдра до параллелепипеда

Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки , не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.

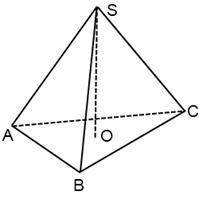
Рисунок 1

Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники. В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды.

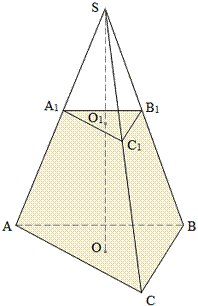
Плоскость, которая пересекает пирамиду и параллельна её основанию, делит её на две части:

пирамиду, подобную данной (SA₁В₁С₁) и

многогранник, называемый усеченной пирамидой (AВСA₁В₁С₁).

Грани усеченной пирамиды, лежащие в параллельных плоскостях (ΔАВС и ΔA₁В₁С₁), называются основаниями, остальные грани (АA₁В₁В, АA₁С₁С, ВВ₁С₁С) называются боковыми гранями.

Основания усеченной пирамиды представляют собой подобные многоугольники, боковые грани – трапеции.

Высота усеченной пирамиды (ОО₁) – это расстояние между плоскостями её оснований.

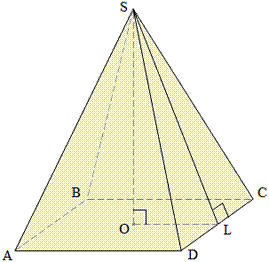
Пирамида (например, SABCD) называется правильной, если ее основанием является правильный многоугольник (ABCD – квадрат), а основание высоты совпадает с центром этого многоугольника (О – центр описанной и вписанной окружностей основания).

Осью правильной пирамиды называется прямая, содержащая ее высоту.

Боковые ребра правильной пирамиды равны.

Боковые грани правильной пирамиды – равные равнобедренные треугольники.

Высота боковой грани правильной пирамиды (SL), проведенная из ее вершины к стороне основания, называется апофемой.

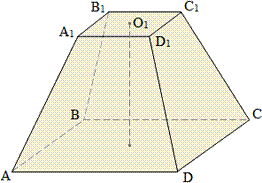
Усеченная пирамида (например, АВСDA₁В₁С₁D₁), которая получается из правильной пирамиды, также называется правильной.

Боковые грани правильной усеченной пирамиды (АA₁В₁В, АA₁С₁С, DD₁С₁С, АA₁D₁D) – равные равнобокие трапеции; их высоты называются апофемами

Сфотографировать письменные ответы и выслать преподавателю