Св-18. Урок 43.. Дата выполнения 27.04.2020г. Задание: выполнить 5 примеров и прислать до 15.00. Равносильность уравнений. Теоремы равносильности. Пример.

27.04.20 Св-18. Урок 43.

Дата выполнения 27.04.2020г. Задание: выполнить 5 примеров и прислать до 15.00

Равносильность уравнений

Показательные уравнения

Логарифмические уравнения

Тригонометрические уравнения

Теоремы равносильности

Два уравнения называются равносильными, если множества их корней совпадают (в том числе, уравнения, не имеющие корней, считаются равносильными).

Теорема 1. Если любое выражение, входящее в уравнение, заменить тождественно равным ему на области определения уравнения выражением, то получим уравнение, равносильное данному.

Теорема 2. Если к обеим частям уравнения прибавить выражение, имеющее смысл на области определения уравнения, то получим уравнение, равносильное данному.

Следствие. Если любое слагаемое перенести из одной части уравнения в другую, поменяв его знак на противоположный, то получим уравнение, равносильное данному.

Теорема 3. Если обе части уравнения умножить (разделить) на выражение, имеющее смысл и отличное от нуля на области определения уравнения, то получим уравнение, равносильное данному.

Уравнение 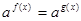(a >0, a≠1)

равносильно f(x) = g(x).

Пример.

Уравнение 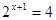преобразуем в уравнение равносильно уравнению

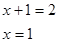
Ответ. 1

Уравнение

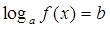равносильно уравнению

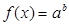, где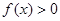

Пример. Уравнение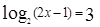

равносильно уравнению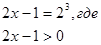

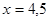Ответ. 4,5

Тригонометрические уравнения, решаемые с помощью тригонометрических формул, сводятся к одному из нескольких типов, решаемые стандартными методами.

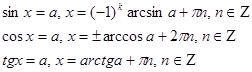
Пример.

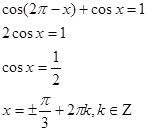
Ответ.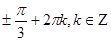

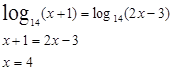Уравнение log_a f(x) = log_a g(x) (f(x) > 0, g(x)>0, a>0, a≠1) равносильно f (x) = g(x). Пример. Проверка. 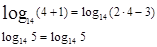Ответ. 4

Равносильность уравнения (1 Б.)

№1.Определи, какому уравнению равносильно уравнение 3x−3=x²−6. (решать не надо)

Ответ:

· lg(x²+3) =lg(2x²+3)

^·1,4 ^3x−3=1,4 ^x2−6

· (2 ^x+3+3)²=(2^x+3)²

· log0,2(x²+3)=log0,2(x²+1)

· 0,4^3x−3=0,4^x2+6

· (x²−3x)³=(2x−3)

№2.Будут ли равносильны уравнения x²−16=0 и x²−5x+4=0? (1 Б2.

№3. Назови посторонний корень уравнения: log₉(2x−5) +log₉(4x−3) =1.

Для определения постороннего корня уравнения вспомним, что для решения используем правило: «сумма логарифмов равна логарифму произведения». При применении этого правила происходит расширение области определения уравнения, значит, проверка корней обязательна.

Проверяя предложенные значения x, получим, что x=0,25 есть посторонний корень, т. к. при этом значении переменной выражение под знаком логарифма будет отрицательным.

№4. Определи: «уравнение 3x−7=9−7x имеет ли корни?»

№5. Назови посторонний корень уравнения: ln(x+4) +ln(2x+3) =ln(1−2x). (3б)

Для решения вспомним:

1.Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:

log_a(bc)=log_ab+log_ac, например lg2+lg5=lg(2⋅5)=lg10=1

2.Уравнение log_a f(x) = log_a g(x)

(f(x)> 0, g(x)>0, a>0, a≠1)

равносильно f (x) = g(x).