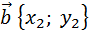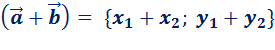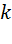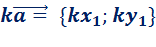- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Понятие вектора. Длина вектора. Равенство векторов
Векторы
на плоскости
Понятие вектора. Длина вектора. Равенство векторов
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется направленным отрезком или вектором.
Любая точка пространства также является вектором, нулевым вектором.


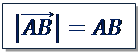
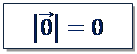
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
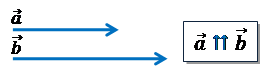 Сонаправленными называют ненулевые коллинеарные векторы
Сонаправленными называют ненулевые коллинеарные векторы
с одинаковыми направлениями.
 |
Противоположно направленными называют ненулевые коллинеарные векторы
с противоположными направлениями.
Векторы называют равными,
если они сонаправлены и их длины равны.
|

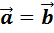 :
:

|
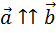
2. 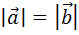
Векторы называют противоположными,
если они противоположно направлены и их длины равны.
|
|

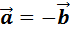 :
:
 1.
1. 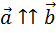
2. 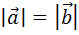
Сложение и вычитание векторов
Сложение векторов
 |
правило треугольника
правило параллелограмма
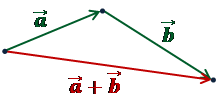
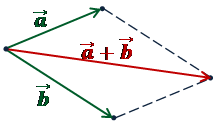
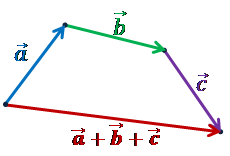 правило многоугольника (ломанной)
правило многоугольника (ломанной)
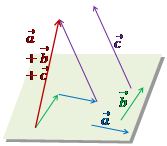 правило многоугольника в пространстве
правило многоугольника в пространстве
Вычитание векторов
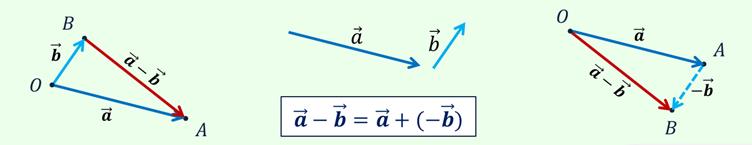
Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам
|
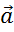 на число
на число 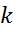 называется такой вектор
называется такой вектор 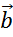 ,
,
длина которого равна  .
.
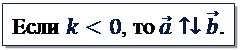


Свойства умножения вектора на число:
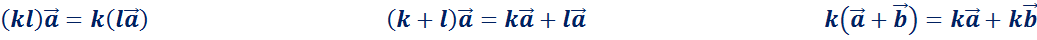
Координаты вектора
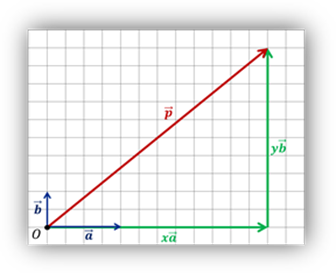
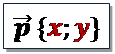
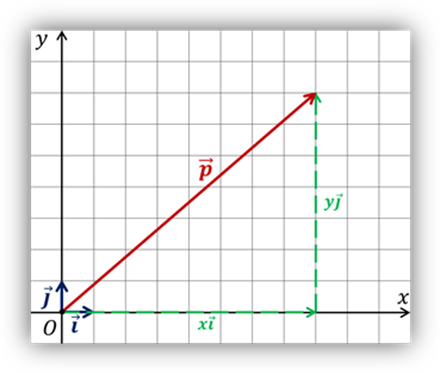

|
| ||||||
| |||||||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|

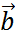
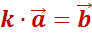
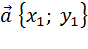 ,
,