- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Действия с векторами.
I. Механика.
1. Основы векторной алгебры.
Вектор – математическая величина, характеризуемая набором величин. Геометрически вектор – направленный отрезок прямой. Вектора равны, если они имеют одинаковую величину и направление: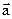 
= 
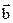Û 
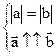. В физике вектор – характеризуется набором 3-х величин: направлением, величиной и точкой приложения. Примеры: сила ( 
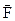), радиус – вектор ( 
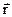), перемещение (Δ 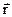), скорость ( 
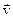), ускорение ( 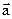) и т.д. Аксеальный вектор –характеризуется только направлением и величиной, направлен вдоль оси вращения Þ точки (•) приложения нет. Примеры: момент силы ( 
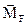), угол поворота (Δ 
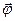), угловая скорость ( 
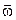), угловое ускорение ( 
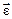) и т.д.
Проекция вектора на ось – скаляр со знаком. Для нахождения проекции аХ вектора 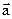на ось Х необходимо опустить перпендикуляры из начала и конца вектора на ось Х, в результате получим точки с координатами Хан и Хак (рис.1). Проекция определится: аХ = Хак – Хан.
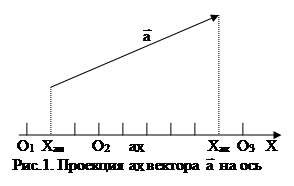аХ > 0 при Хак > Хан; аХ < 0 при Хак < Хан; аХ = 0 при Хак = Хан ( 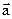׀ X).
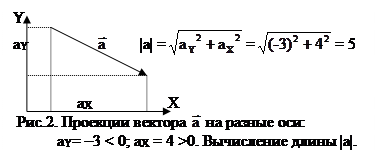
Определим проекцию аХ для рис.1 относительно разных начал координат.
О1: аХ = 8 – 1 = 7 > 0; О2: аХ = 5 – (– 2) = 7 > 0; О3: аХ = – 1 – (– 8) = 7 > 0.
Действия с векторами.
1. Сложение векторов. Для нахождения суммы нескольких векторов необходимо один из них взять за первый, к его концу пристроить следующий и т.д. Сумма – это вектор с началом в начале первого и концом в конце последнего (рис.3а и 3б). В частном случае для сложения 2-х векторов является правило параллелограмма (рис.3с).
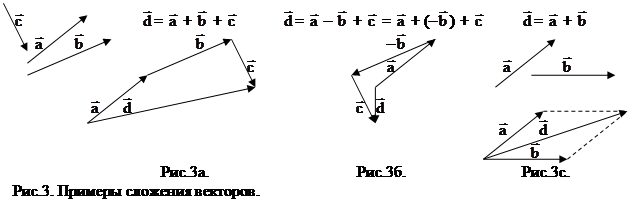
Длину |d| можно определить по формулам геометрии и через проекции |d| =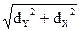 
,
где: dY = aY + bY + cY, dX = aX + bX + cX.
2. Умножение векторов.
2.1. Умножение вектора на скаляр = вектор: 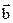= m ∙ .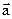
m > 0 Û 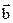↓↓ 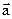; m < 0 Û 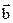↓↑ 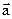; |m| > 1 Û |b| >|a|; |m| < 1 Û |b| <|a|.
2.2. Умножение вектора на вектор.
2.2.1. Скалярное умножение векторов = скаляр со знаком: с = 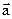∙ 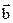= |a| ∙ |b| ∙ cos( 
).
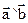Свойства: 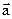∙ 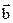= 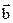∙ 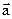, т.к. cosα = cos(–α) – чётная.
Физический смысл: с – это работа силы 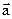( 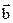) на перемещении ( ).
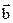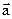2.2.2. Векторное умножение векторов = вектор: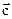 
= × = [ ; ].
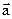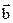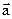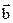сХ = |a| ∙ |b| ∙ sin( ).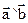
Свойство: 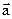× 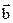= – 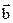× 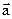, т.к. sin(–α) = – sinα – нечётная.
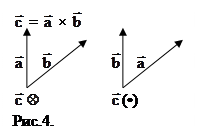
Вектор 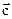направлен в сторону поступательного движения оси правого винта (рис.4).
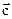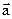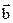Физический смысл. = × – момент силы 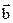с радиус –
вектором .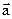
Геометрический смысл: |с| = S параллелограмма,
построенного на векторах 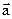и 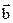(рис.3с).
3. Деление векторов. Вектор на вектор не делится.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|