Контакты

Случайная статья

Тригонометрические уравнения

Тригонометрические уравнения

Напомним, что тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.

Уравнения вида

, , , ,

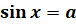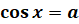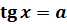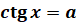где 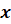– переменная, 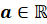, называются простейшими тригонометрическими уравнениями.

При рассмотрении тригонометрических уравнений тем или иным способом решение сводят к простейшим уравнениям, которые в общем случае решаются по следующим формулам:

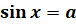
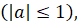
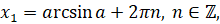
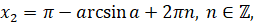
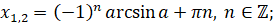
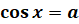
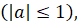
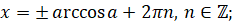
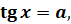
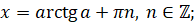
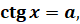
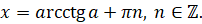
В частных случаях пр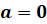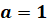и , и 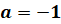получаются следующие формулы:

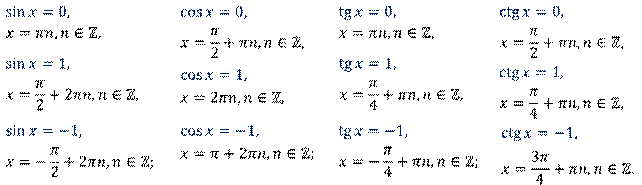
Уравнения вида

, , , ,

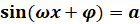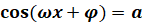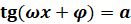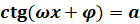где 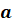, , 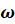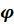принадлежат действительным числам также относятся к простейшим. Их следует решать по общим формулам, заменив 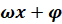на 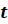, и уже после этого находить 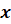из равенства .

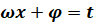Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задание первое. Решите уравнения:

а) 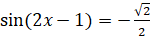, б) .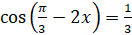

Решение.

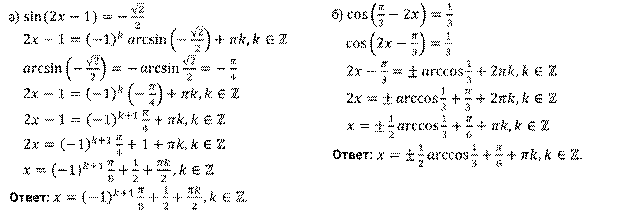
Задание второе. Решите уравнения методом разложения на множители:

а) 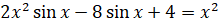, б) .

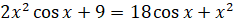Решение.

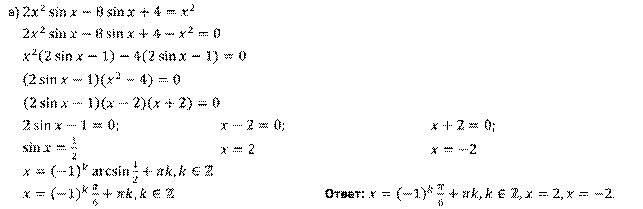
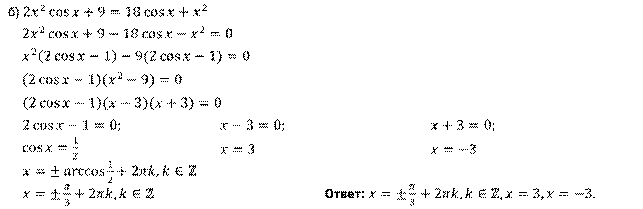
Задание третье. Решите уравнения:

а) 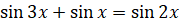, б) .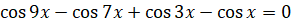

Решение.

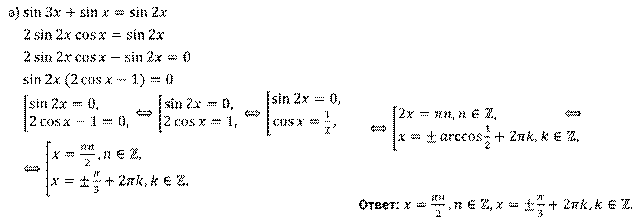
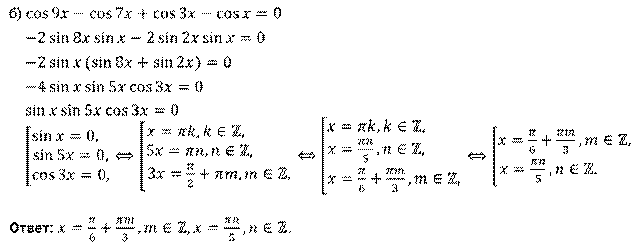
Задание четвёртое. Решите уравнения:

а) 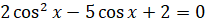, б) .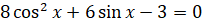

Решение.

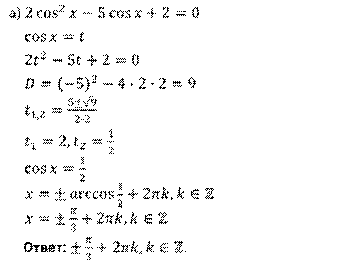
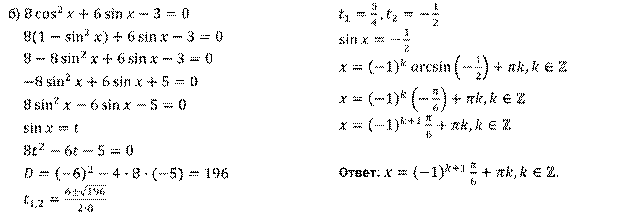
Задание пятое. Решите уравнение .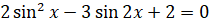

Решение.

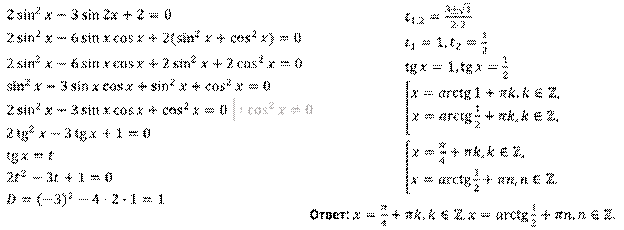
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.