Табличный» метод

. «Табличный» метод

Рассмотрим алгоритм симплексного метода.

1. Математическая модель задачи должна быть канонической. Если она неканоническая, то ее надо привести к каноническому виду. Предположим, что все дополнительные переменные имеют тот же знак, что и свободные члены. То есть первое же базисное решение является допустимым.

2. Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем симплексную таблицу (табл. 2). Все строки таблицы 1-го шага, за исключением строки 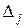(индексная строка), заполняем по данным системы ограничений и целевой функции.

Таблица 2

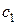
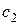
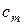
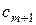
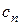
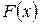
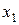
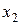
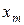
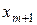
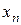
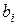
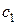
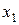
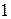
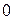
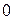
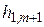
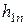
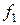
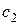
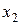
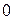
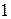
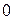
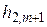
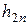
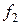
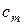
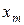
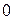
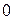
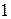
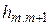
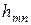
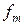
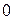
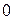
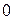
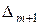
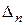
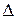
Индексная строка для переменных находится по формуле:

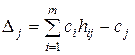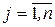, , (22)

и по формуле:

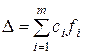, (23)

для свободного члена.

Возможны следующие случаи при решении, например, задачи на максимум:

а) если все оценки 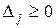, то найденное решение оптимальное;

б) если хотя бы одна оценка 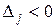, но при соответствующей переменной нет ни одного положительного коэффициента (в столбце), решение задачи прекращаем, так как 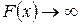, т.е. целевая функция неограничена в области допустимых решений;

в) если хотя бы одна оценка отрицательная, а при соответствующей переменной есть хотя бы один положительный коэффициент, то нужно перейти к другому опорному решению;

г) если отрицательных оценок в индексной строке несколько, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная оценка.

Таким образом, если хотя бы одна оценка 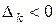, то 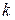-й столбец принимаем за ключевой. За ключевую строку принимаем ту, которой соответствует минимальное отношение свободных членов 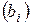к положительным коэффициентам 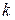-го столбца. Элемент, находящийся на пересечении ключевой строки и столбца, называется ключевым элементом.

3. Заполняем симплексную таблицу 2-го шага:

а) переписываем ключевую строку, разделив ее на коэффициент при ключевом элементе;

б) заполняем базисные столбцы;

в) остальные коэффициенты таблицы находим по правилу «прямоугольника». Оценки можно считать по приведенным выше формулам или по правилу «прямоугольника». Получаем новое опорное решение, которое проверяем на оптимальность и т.д.

Правило «прямоугольника» заключатся в следующем. Пусть, например, ключевым элементом 1-го шага является элемент 1-й строки 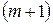-го столбца 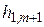. Тогда элемент 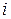-й строки 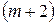-го столбца 2-го шага – обозначим его 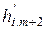- согласно правилу «прямоугольника» выражается формулой:

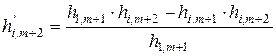где 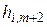, , 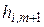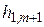- элементы 1-го шага.