Тема 1.3. Системы случайных величин

Тема 1.3. Системы случайных величин

Пример 1. Задано распределение двумерной случайной величины:

Найти распределения X, Y и X + Y.

Решение.В нашем случае возможные значения случайной величины X:

х₁ = 1, x₂ = 2, х₃ = 3. Тогда, согласно формуле (15.22), имеем Р(х₁)= 0,1 + 0,2 = 0,3, Р(х₂) =0,15 +0,22 = = 0,37, Р(х₃) =0,12 +0,21 =0,33. Отсюда получаем закон распределения X:

X 1 2 3

р 0,3 0,37 0,33. М(Х)=1*0,3+2*0,37+3*0,33=2,03 D(X) = М(Х²) - [М(Х)}²

Аналогично получаем и для распределения Y: у₁ = 1, у₂ = 2;

Р(_У1) = 0,1 + 0,15 + 0,12 = 0,37, Р(у₂) = 0,2 + 0,22 + 0,21 = 0,63;

Y 1 2

р 0,37 0,63. М(У)=1*0,37+2*0,63=1,63

Теперь найдем распределение X+Y. Возможные значения этой случайной величины: 2, 3, 4 и 5. Соответствующие вероятности

Р(2) = 0,1, Р(3) = 0,15 + 0,2 = 0,35, Р(4) = 0,12 + 0,22 = 0,34, Р(5) = 0,21. Отсюда находим искомое распределение:

X+Y 2 3 4 5

р 0,1 0,35 0,34 0,21.

В случае системы двух случайных величин используются кроме математических ожиданий и дисперсий еще и другие числовые характеристики, описывающие их взаимосвязь.

Пример 2. Найти корреляционный момент и коэффициент корреляции двух случайных величин X и У, распределения которых заданы в предыдущем примере 1.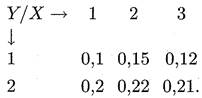

Решение.Воспользуемся формулами (15.24),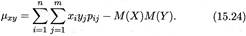

(15.26),

атакже формулой вычисления центрального момента второго порядка (15.19);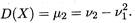

последовательно вычисляем: М(Х)=0,1+0,2+0,3+0,44+0,36+0,63=2,03, М(У)=0,1+0,15+0,12+0,4+0,44+0,42=1,63,

М(Х²)=0,1+0,2+0,6+0,88+1,08+1,89=4,75

{М(Х)}² =4,1209,

D(X) = D(X) = М(Х²) - [М(Х)}²=4,75-4,1209=0,629, D(Y) = 0,233,

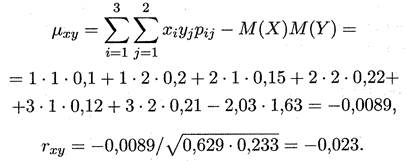В данном случае коэффициент корреляции близок к нулю; это означает, что случайные величины X и У слабокоррелированы.

Пример 3. Найти линейную среднюю квадратическую регрессию и остаточную дисперсию случайной величины Y на случайную величину X по данным примеров 1 и 2.

РЕШЕНИЕ. Для двумерной случайной величины (X, Y), приведенной в примере 1, все необходимые числовые характеристики указаны в решении примера2: т_х= 2,03, т_у= 1,63, r_ху =-0,023, σ_х= √D(X)=0,793, σ_у= √D(Y) =0,483. Из уравнения(15.28)

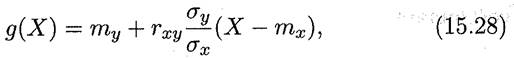
получаем искомое соотношение:

g(Х) =1,63 - 0,014(Х - 2,03).

Остаточная дисперсия рассчитывается по формуле:

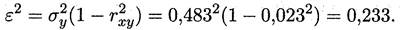Для оценки среднеквадратичной погрешности линейной регрессии обычно используют величину σ_у, в нашем случае она составляет σ_у = 0,483.

Пример решить самостоятельно

Задано распределение двумерной случайной величины:

Y/X
	0,11	0,16	0,13
	0,21	0,23	0,22

Найти линейную среднюю квадратическую регрессию и остаточную дисперсию случайной величины Y на случайную величину X