Контакты

Случайная статья

Тема урока:Арифметический корень натуральной степени

Тема урока:Арифметический корень натуральной степени

Цели урока:дидактическая: обобщение знаний о корнях и арифметических корнях, познакомить со свойствами арифметического корня; подготовить к изучению понятия степени с действительным показателем; научить применять полученные знания при решении заданий , стимулировать учащихся к овладению приемами, которые будут полезны в дальнейшем, в частности при решении уравнений;

развивающая: развивать логическое мышление, память, продолжать формирование математической речи, вырабатывать умение анализировать и сравнивать;

Решим задачу.

Площадь квадрата S=16 м².

Обозначим сторону квадрата а, м.

Тогда, а² = 16.

Решим данное уравнение:

a=4и а= –4.

Проверим решение:

4² = 16;

(–4)² = 16.

Ответ: длина стороны квадрата равна 4 м.

Определение:

Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.

Определение:

Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.

Обозначение: .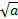

Определение:

Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.

Обозначение: .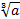

Например:

.

.

.

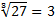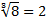На основании определений квадратного и кубического корней, можно сформулировать определения корня n-ой степени и арифметического корня n-ой степени.

Определение:

Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.

Определение:

Арифметическим корнем натуральной степени, где n≥2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.

Обозначение: 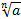– корень n-й степени, где

n–степень арифметического корня;

а– подкоренное выражение.

Давайте рассмотрим такой пример: .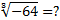

Мы знаем, что (–4)³ = –64, следовательно, .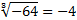

Еще один пример: .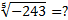

Мы знаем, что (–3)⁵ = –243, следовательно, .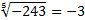

На основании этих примеров, можно сделать вывод:

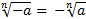, при условии, что n –нечетное число.

Свойства арифметического корня натуральной степени:

Если а ≥ 0, b ≥ 0 и n, m – натуральные числа, причем n ≥ 2, m ≥ 2, то справедливо следующее:

1. .

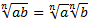Примеры:

.

.

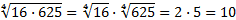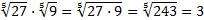1. .

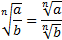Примеры:

.

.

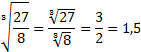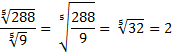1. .

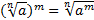Пример:

.

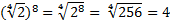1. .

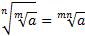Пример:

.

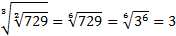1. Для любогоа справедливо равенство:

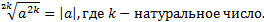
Пример:

Найдите значение выражения 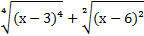, при 3 <x< 6.

Степени заданных арифметических корней 4 и 2, четные числа, следовательно, мы можем применить свойство №5:

=|x – 3| = х – 3, т.к. х>3;

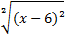=|x – 6|=6 – x, т.к. х<6.

Получаем: х – 3 + 6 – х= 3.

Итог урока

Свойства корня натуральной степени:

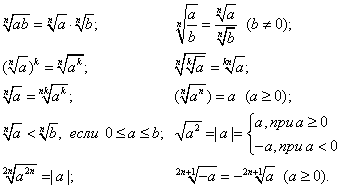
Домашнее задание

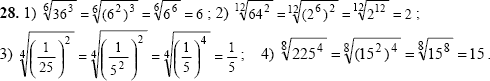
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.