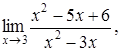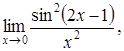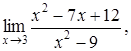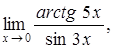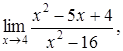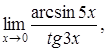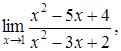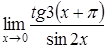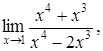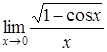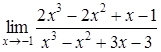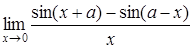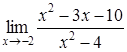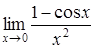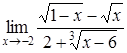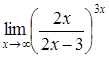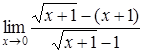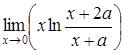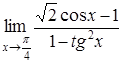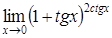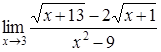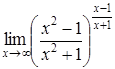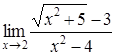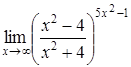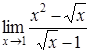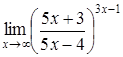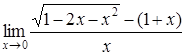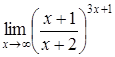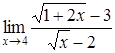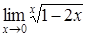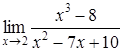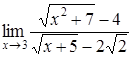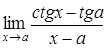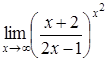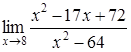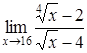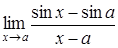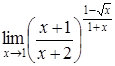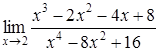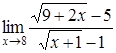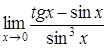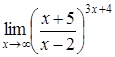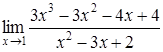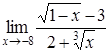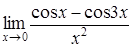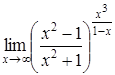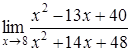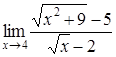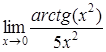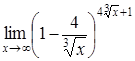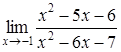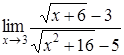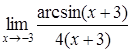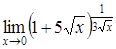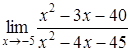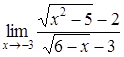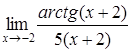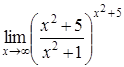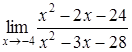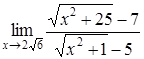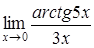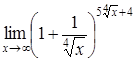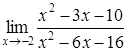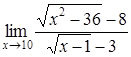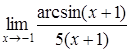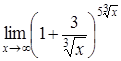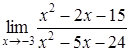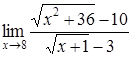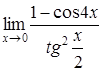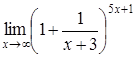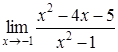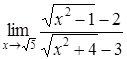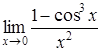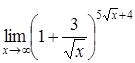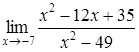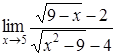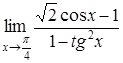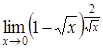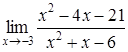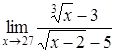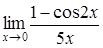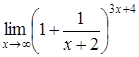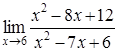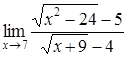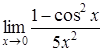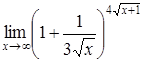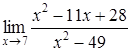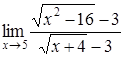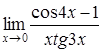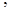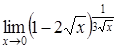- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
математика 1 страница
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
Государственная организация высшего профессионального образования «Донецкий национальный университет экономики
и торговли имени Михаила Туган-Барановского»
Кафедра высшей и прикладной математики
И.В. Гречина
математика
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Для внеаудиторной контрольной работы
для обучающихся по экономическим специальностям
ОП ВПО - программа бакалавриата
Донецк – 2020
варианты индивидуальных заданий.
Номер варианта определяется по номеру в списке группы в журнале.
1. Решить систему линейных уравнений методами: Крамера; обратной матрицы; Гаусса.
1.1. 
| 1.2. 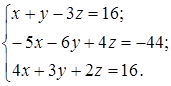
| 1.3. 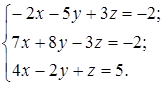
|
1.4. 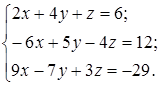
| 1.5. 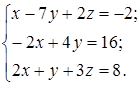
| 1.6. 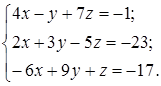
|
1.7. 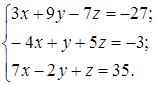
| 1.8. 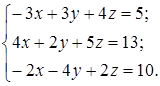
| 1.9. 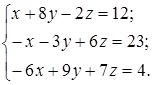
|
1.10. 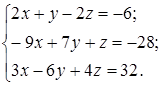
| 1.11. 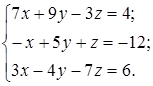
| 1.12. 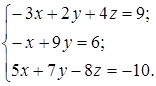
|
1.13. 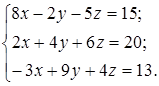
| 1.14. 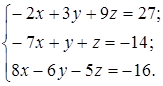
| 1.15. 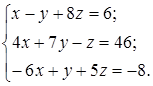
|
1.16. 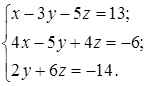
| 1.17. 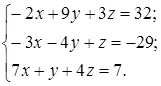
| 1.18. 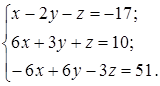
|
1.19. 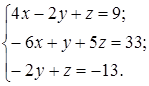
| 1.20. 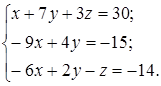
| 1.21. 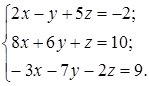
|
1.22. 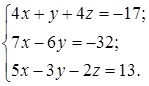
| 1.23. 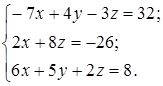
| 1.24. 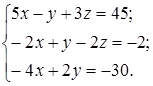
|
1.25. 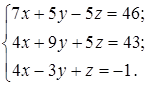
| 1.26. 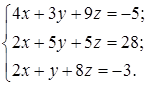
| 1.27. 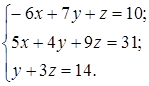
|
1.28. 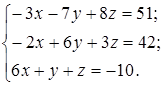
| 1.29. 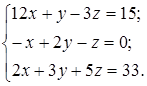
| 1.30. 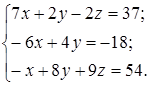
|
2. По координатам вершин пирамиды 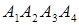 с помощью векторной алгебры найти:
с помощью векторной алгебры найти:
· длину стороны 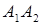 ,
,
· косинус угла между ребрами 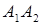 и
и 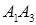 ,
,
· объем пирамиды 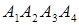 ,
,
· работу силы, которая есть равнодействующей сил F1 и F2, под действием которой тело перемещается прямолинейноиз точки А1 в току А2.
| 2.1. | 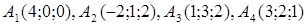 , , 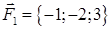 , , 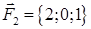
|
| 2.2. | 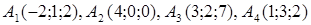 , , 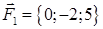 , , 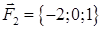
|
| 2.3. | 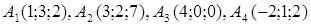 , , 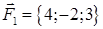 , , 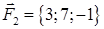
|
| 2.4. | 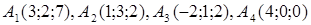 , , 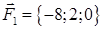 , , 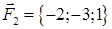
|
| 2.5. | 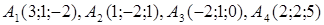 , , 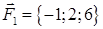 , , 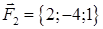
|
| 2.6. | 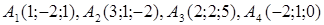 , , 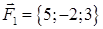 , , 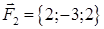
|
| 2.7. | 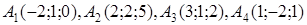 , , 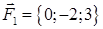 , , 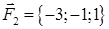
|
| 2.8. | 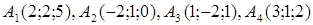 , , 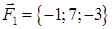 , , 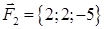
|
| 2.9. | 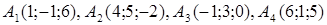 , , 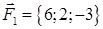 , , 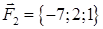
|
| 2.10. | 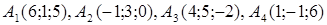 , , 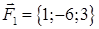 , , 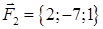
|
| 2.11. | 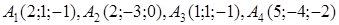 , , 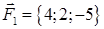 , , 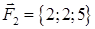
|
| 2.12. | 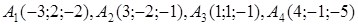 , , 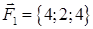 , , 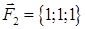
|
| 2.13. | 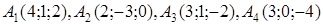 , , 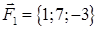 , , 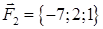
|
| 2.14. | 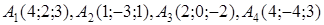 , , 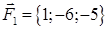 , , 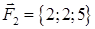
|
| 2.15. | 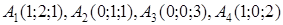 , , 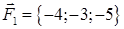 , , 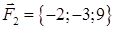
|
| 2.16. | 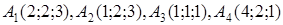 , , 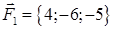 , , 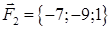
|
| 2.17. | 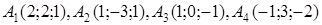 , , 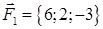 , , 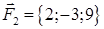
|
| 2.18. | 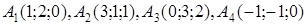 , , 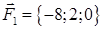 , , 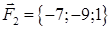
|
| 2.19. | 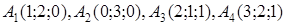 , , 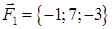 , , 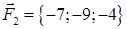
|
| 2.20. | 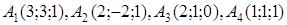 , , 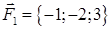 , , 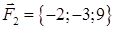
|
| 2.21. | 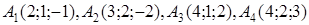 , , 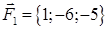 , , 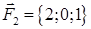
|
| 2.22. | 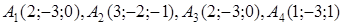 , , 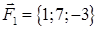 , , 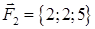
|
| 2.23. | 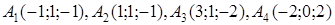 , , 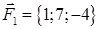 , , 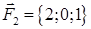
|
| 2.24. | 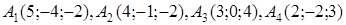 , , 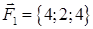 , , 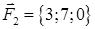
|
| 2.25. | 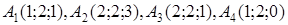 , , 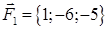 , , 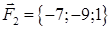
|
| 2.26. | 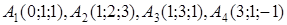 , , 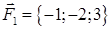 , , 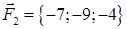
|
| 2.27. | 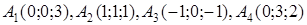 , , 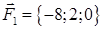 , , 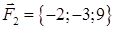
|
| 2.28. | 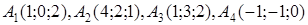 , , 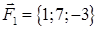 , , 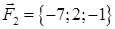
|
| 2.29. | 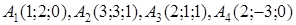 , , 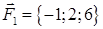 , , 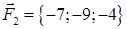
|
| 2.30. | 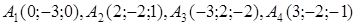 , , 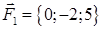 , , 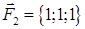
|
3. По координатам вершин треугольника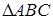 найти:
найти:
· уравнение линии 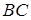 ,
,
· уравнение высоты 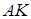 ,
,
· длину высоты 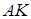 .
.
| 3.1. | А(0;3), В(2;4), С(-8;-1) | 3.2. | А(1;-3), В(3;-5), С(-5;7) |
| 3.3. | А(2;-1), В(4;2), С(5;1) | 3.4. | А(9;6), В(-7;-6), С(0;18) |
| 3.5. | А(1;1), В(7;4), С(4;5) | 3.6. | А(-1;1), В(-7;4), С(-4;5) |
| 3.7. | А(-1;-1), В(-7;2), С(-4;3) | 3.8. | А(1;-1), В(-5;2), С(-2;3) |
| 3.9. | А(7;1), В(-5;-4), С(-9;-1) | 3.10. | А(1;0), В(7;3), С(4;4) |
| 3.11. | А(1;-1), В(7;2), С(4;5) | 3.12. | А(-1;1), В(5;4), С(2;5) |
| 3.13. | А(-2;1), В(-18;-11), С(-11;13) | 3.14. | А(-1;-1), В(5;2), С(2;3) |
| 3.15. | А(10;-1), В(-2;-6), С(-6;-3) | 3.16. | А(0;1), В(6;4), С(3;5) |
| 3.17. | А(4;3), В(-12;-9), С(-5;15) | 3.18. | А(6;2), В(30;-5), С(12;19) |
| 3.19. | А(1;1), В(-15;11), С(-8;13) | 3.20. | А(-1;7), В(11;2), С(17;10) |
| 3.21. | А(-14;10), В(10;3), С(-8;27) | 3.22. | А(-12;6), В(12;-1), С(-6;23) |
| 3.23. | А(3;-5), В(4;1), С(5;-2) | 3.24. | А(8;0), В(-4;-5), С(-8;-2) |
| 3.25. | А(-2;7), В(3;-3), С(2;5) | 3.26. | А(11;4), В(-1;-1), С(5;7) |
| 3.27. | А(20;5), В(-4;12), С(-8;9) | 3.28. | А(21;5), В(-3;-2), С(-7;11) |
| 3.29. | А(-5;2), В(2;-1), С(1;-2) | 3.30. | А(1;1), В(-5;4), С(-2;5) |
4. Найти пределы:
| 4.1. | a) | b) 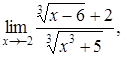
| ||
| c) | d) 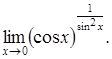
| |||
| 4.2. | a) | b) 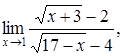
| ||
| c) | d) 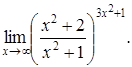
| |||
| 4.3. | a) | b) 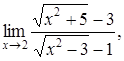
| ||
| c) | d) 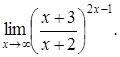
| |||
| 4.4. | a) | b) 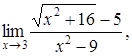
| ||
| c) | d) 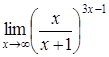 
| |||
| 4.5. | a) | b) 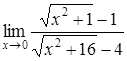 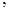
| ||
| c) | d) 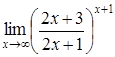 
| |||
| 4.6. | a) | b) 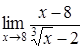 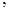
| ||
| c) | d) 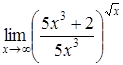 
| |||
| 4.7 | a) | b) 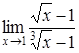 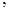
| ||
| c) | d) 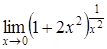 
| |||
| 4.8. | a) 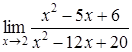 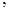
| b) | ||
c) 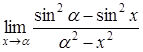 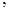
| d) | |||
| 4.9. | a) 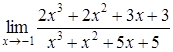 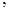
| b) | ||
c) 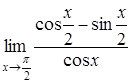 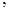
| d) | |||
| 4.10. | a) 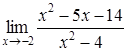 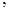
| b) | ||
c) 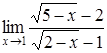 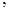
| d) | |||
| 4.11. | a) 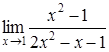 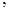
| b) | ||
c) 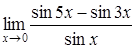 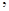
| d) | |||
| 4.12. | a) 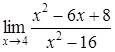 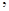
| b) | ||
c) 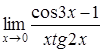 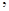
| d) | |||
| 4.13. | a) 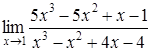 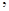
| b) | ||
c) 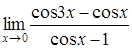 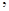
| d) | |||
| 4.14. | a) 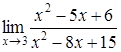 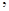
| b) | ||
c) 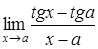 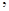
| d) | |||
| 4.15. | a) 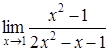 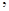
| b) | ||
c) 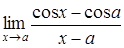 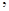
| d) | |||
| 4.16. | a) | b) | ||
| c) | d) | |||
| 4.17. | a) | b) | ||
| c) | d) | |||
| 4.18. | a) | b) | ||
| c) | d) | |||
| 4.19. | a) | b) | ||
| c) | d) | |||
| 4.20. | a) | b) | ||
| c) | d) | |||
| 4.21. | a) | b) | ||
| c) | d) | |||
| 4.22. | a) | b) | ||
| c) | d) | |||
| 4.23. | a) | b) | ||
| c) | d) | |||
| 4.24. | a) | b) | ||
| c) | d) | |||
| 4.25. | a) | b) | ||
| · | · | |||
| 4.26. | 1) | 2) | ||
| 3) | 4) | |||
| 4.27. | 1) | 2) | ||
| 3) | 4) | |||
| 4.28. | § | § | ||
| § | § | |||
| 4.29. | 1) | 2) | ||
| 3) | 4) | |||
| 4.30. | 1) | 2) | ||
| 3) | 4) | |||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|