Теорема о изменении количества движения системы

Задача 3

Теорема о изменении количества движения системы

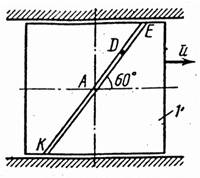
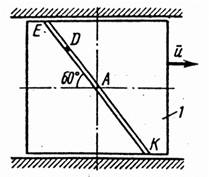
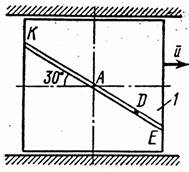
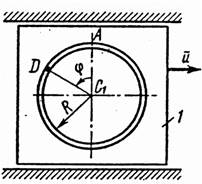
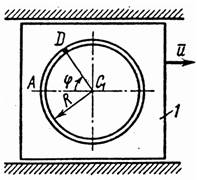
Механическая система состоит из прямоугольной вертикальной плиты 1 массой m₁, движущейся вдоль горизонтальных направляющих, и груза D массой т₂ (рис.1 – 0, табл. 1). В момент времени t_o= 0, когда скорость плиты u_о , груз под действием внутренних сил начинает двигаться по желобу плиты.

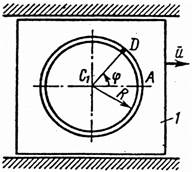
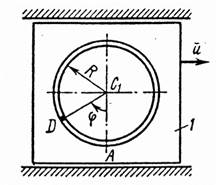
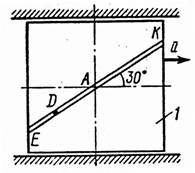
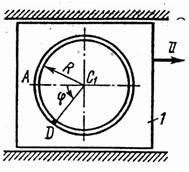
На рис. 0–4 желоб КЕ прямолинейный и при движении груза расстояние s = AD изменяется по закону s = f₁(t), а на рис. 5–0 желоб – окружность радиуса R = 0,8 м и при движении груза угол j = ÐАС₁D изменяется по закону j = f₂(t), В табл. Д4 эти зависимости даны отдельно для рис. 0 и 1; для рис. 2 и 3 и т. д., где s выражено в метрах, j – в радианах, t – в секундах.

Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить зависимость и = f(t), т. е. скорость плиты как функцию времени.

Данные таблицы 1 выбираются по последней цифре номера зачетки

Таблица 1

Номер условия	s = f₁(t)		j = f₂(t)
Номер условия	Рис. 1	Рис. 2,3,4	Рис. 5,6	Рис. 7,8,9,0

	0,6sin(pt²)	1,4(3t² – 2)	p(3 – 2t²)/4	p(2t² – 2)
	1,4cos(pt/2)	1,6sin(pt²/2)	p(1 – 3t²)/5	p(1–4t²)/5
	1,6(3t² – 1)	0,4cos(pt)	p(t²– 6)/4	p(3 + 4t²)/3
	1,4sin(pt²/3)	0,8sin(pt²/6)	p(4 – t²)	p(t² + 1)/4
	1,5cos(pt/6)	0,2cos(pt/3)	p(2+ 7t²)/6	p(1 – 5t²)/8
	0,8sin(pt²/4)	1,5(3 – 4t²)	p(7t² +1)/6	p(t² – 4)/5
	1,8(4 – 3t²)	0,5sin(pt²/3)	p(t² – 4)/5	pt²/2
	0,9cos(pt/3)	1,4cos(pt/4)	p(5 + t²)/4	p(7t² – 1)/8
	0,2sin(pt²/5)	1,8sin(pt²)	pt²/4	p(t² + 5)/6
	1,8cos(pt/4)	2,6cos(pt/6)	p(t² + 4)/8	p(4 – t²)/2

Номер чертежа выбирается по предпоследней цифре номера зачетки


Рис. 1		Рис. 2

Рис. 3	Рис. 4		Рис. 5

Рис. 6	Рис. 7		Рис. 8

Рис. 9		Рис. 0

Масса плиты и масса груза выбираются по последней цифре номера зачетки

Номер варианта	0	1	2	3	4	5	6	7	8	9
m₁( кг)	6	10	12	11	4	5	6	3	5	2
т₂( кг)	2	3	4	5	9	8	7	6	5	4

12 Следующая ⇒