октября 2020 г. (четверг)

Цель:

Учебная: рассмотреть основные понятия стереометрии, изучить математическую символику.

Развивающая: развивать математическое мышление, графические навыки, пространственное воображение.

Воспитательная: воспитывать у обучающихся устойчивый интерес к изучению математики; математическую культуру.

Литература: Геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / Л.С. Атанасян, В.Ф. Бутузов [и др.] – М.: Просвещение, 2013.

Материалы урока:

Пишем в конспектах:

Геометрия – это наука о свойствах геометрических фигур. Геометрия состоит из двух частей: планиметрии и стереометрии.

Планиметрия – это раздел геометрии, в котором изучаются геометрические фигуры на плоскости.

Стереометрия – это раздел геометрии, в котором изучаются фигуры в пространстве.

Геометрические фигури – это абстрактные фигуры, напоминающие предметы, которые нас окружают.

Аксиома (утверждение, не вызывающее сомнений) – это утверждение, которое принимается истинным без доказательства. Утверждение, истинность которого устанавливается путём доказательства и которое используется для доказательства других утверждений, называют теоремой. Теорема состоит из двух частей: условия и заключения.

Определение – это утверждение, которое описывает существенные свойства предмета (понятия), что даёт возможность отличать его от других.

Точку, прямую, плоскость называют неопределёнными, или начальными (с которых всё начинается), или основными понятиями стереометрии. Точки обозначают большими буквами латинского алфавита – А, В, С... (рисуем точку); прямые – а, b, с... или АВ, СD... (рисуем отрезок); плоскости – α, β, γ... или (АВС), (ВСD)... (рисуем параллелограмм).

Плоскость мы представляем себе как ровную поверхность крышки стола и поэтому будем изображать её в виде параллелограмма. Плоскость, как и прямая, бесконечна. На рисунке мы изображаем только часть плоскости , но представляем себе её неограниченно продолженной во все стороны.

АКСИОМЫ ПЛАНИМЕТРИИ.

Аксиомы принадлежности: 1) Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. 2) Через любые две точки можно провести прямую, и только одну.

Аксиомы расположения: 1) Из трёх точек на прямой одна и только одна лежит между двумя другими. 2) Прямая разбивает плоскость на две полуплоскости.

Аксиомы измерения: 1) Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой. 2) Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180^о. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Аксиомы откладывания: 1) На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один. 2) От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180^о, и только один. 3) Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Аксиома параллельности: Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

МатематичЕСКАЯ символИка.

Î – принадлежит; 

А  b – точка А принадлежит прямой b;

b Ì γ – прямая b принадлежит плоскости γ;

Ï – не принадлежит; 

Ç – пересекаются;

AB Ç AC = А – прямые AB и AC пересекаются в точке A;

(ABC) Ç (ACD) = АС – плоскости (ABC) и (ACD) пересекаются по прямой AC;

= – равны, совпадают;

а = b – прямые а и b совпадают;

¹ – не равны, не совпадают, различны;

b 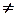 с – прямые b и с различны;

Þ – знак следования;

|| – параллельны;

а || b – прямые а и b параллельны;

 ^ – перпендикулярны;

β ^ γ– плоскости β и γ перпендикулярны;

Домашнее задание: выучить математическую символику.

Самостоятельная учебная работа:

изучить теоретический материал стр. 3-4.

ФОТОГРАФИРУЕМ И ОТСЫЛАЕМ ЕЛЕНЕ АНАТОЛЬЕВНЕ

ВСЕ ВЫПОЛНЕННЫЕ ДОМАШНИЕ ЗАДАНИЯ И КОНТРОЛЬНЫЕ РАБОТЫ!!!!!!!!