Кванторные операции.. Квантор всеобщности.

Кванторные операции.

Рассмотрим операции, преобразующие предикаты в высказывания.

Пусть имеется предикат Р(х) определенный на множестве М. Если “а” – некоторый элемент из множества М, то подстановка его вместо х в предикат Р(х) превращает этот предикат в высказывание Р(а). Такое высказывание называют единичным. Например, r(x): “х – четное число” – предикат, а r (6)- истинное высказывание, r (3) – ложное высказывание.

Это же относится и к n – местным предикатам: если вместо всех предметных переменных х_i, i= 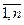подставить их значения, то получим высказывание.

Наряду с образованием из предикатов высказываний в результате таких подстановок в логике предикатов рассматриваются еще две операции, которые превращают одноместный предикат в высказывание. Эти операции называются операциями квантификации (или просто квантификацией, или связыванием кванторами, или навешиванием кванторов). При этом рассматриваются, соответственно, два типа так называемых кванторов.

1.1 Квантор всеобщности.

Пусть Р(х) – предикат, определенный на множестве М. Под выражением понимают высказывание, истинное, когда Р(х) истинно для каждого элемента х из множества М, и ложное в противном случае. Это высказывание уже не зависит от х. Соответствующее ему словесное выражение звучит так: “Для всякого х Р(х) истинно ”.

Символ называют квантором всеобщности (общности). Переменную х в предикате Р(х) называют свободной (ей можно придавать различные значения из М), в высказывании же х называют связанной квантором всеобщности.

12 3 Следующая ⇒