Треугольники

Треугольники

1. В равнобедренном треугольнике высота, проведенная к основанию, равна 5, а периметр треугольника равен 50. Найти площадь треугольника.

2. В прямоугольном треугольнике медианы, проведенные к катетам, равны 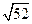и 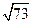. Найти гипотенузу треугольника.

3. В треугольнике, две стороны которого равны 17 и 25, высота делит третью сторону на отрезки, разность длин которых равна 12. Найти периметр треугольника.

4. В прямоугольном треугольнике один из катетов равен 13, а высота, опущенная на гипотенузу, равна 12. Найти площадь этого треугольника.

5. Катеты прямоугольного треугольника относятся как 1:3, а гипотенуза равна 40. Найти длину высоты, опущенной на гипотенузу.

6. В равнобедренном треугольнике основание равно 1, высота, опущенная на основание, равна . Найти расстояние от середины основания до боковой стороны.

7. Периметр прямоугольного треугольника равен 60, а высота, проведенная к гипотенузе, равна 12. Найти радиус окружности, описанной около этого треугольника.

8. Периметр прямоугольного треугольника АВС 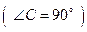равен 72, а разность между длинами медианы СК и высоты СМ равна 7. Найти длину медианы.

9. Найти длину катета, лежащего против угла в 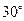в прямоугольном треугольнике, если площадь треугольника равна .

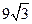10. В квадрате, сторона которого равна 4, середины двух смежных сторон соединены между собой и с противоположной вершиной квадрата. Найти площадь полученного внутреннего треугольника.

11. Стороны треугольника относятся как 3:4:5, а его площадь равна 54. Найти периметр треугольника.

12. На сколько процентов нужно увеличить длины сторон треугольника, чтобы его площадь стала больше на 69% ?

13. Треугольник, периметр которого равен 15, делится медианой на два треугольника с периметрами 11 и 14. Найти длину этой медианы.

14. Медиана прямоугольного треугольника, проведенная к гипотенузе, разбивает его на два треугольника с периметрами 16 и 18. Найти длину гипотенузы.

15. Внутренние углы треугольника относятся как 2:6:4. Найти внешний угол треугольника, смежный с меньшим внутренним.

16. В треугольнике АВС величина внешнего угла при вершине В в три раза больше величины угла А и на 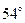больше величины угла С. Найти угол А.

17. Один внутренний угол треугольника равен 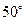, а сумма другого угла и угла, смежного с третьим, равна . Найдите величину третьего угла.

18. Величина одного из углов треугольника равна 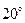. Найти острый угол между биссектрисами двух других углов треугольника.

19. В треугольнике АВС угол А равен 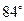, угол В равен 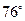. Найти (в градусах) угол между биссектрисой угла А и высотой, опущенной на сторону ВС.

20. Если в равнобедренном треугольнике угол при вершине равен 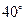, то угол между основанием и высотой, проведенной к боковой стороне, равен…

21. Биссектриса внешнего угла при основании равнобедренного треугольника образует с основанием угол 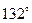. Найти угол при вершине треугольника.

22. Определить площадь прямоугольного треугольника, если известна гипотенуза 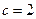и сумма синусов острых углов .

23. В прямоугольном треугольнике гипотенуза равна 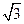, а биссектриса одного из острых углов равна 1. Найти больший катет треугольника.

24. Высота прямоугольного треугольника, опущенная на гипотенузу, равна 2, а острый угол равен 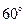. Найти гипотенузу треугольника.

25. В треугольнике АВС проведена высота ВD. 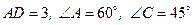. Найти ВС.

26. Высота, проведенная из вершины прямого угла треугольника, делит угол в отношении 1:2. В каком отношении она делит площадь треугольника?

27. В прямоугольном треугольнике АВС из вершины прямого угла В проведена высота ВР. Если выполнено условие 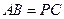, то косинус угла А равен…

28. В треугольнике АВС 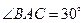. Найти сторону ВС, если .

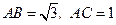29. В треугольнике АВС: 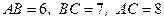. Найти .

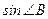30. В треугольнике АВС: 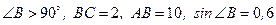. Найти АС.

31. В равнобедренном треугольнике к боковой стороне длины 4 проведена медиана, длина которой равна 3. Найти периметр треугольника.

32. Основание равнобедренного треугольника равно , а медиана боковой стороны равна 5. Найти длину боковой стороны.

33. 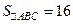. Найти АВ, если .

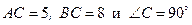34. В треугольнике АВС: . На стороне АВ отмечена точка М такая, что 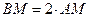, а на стороне ВС – такая точка К, что 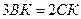. Найти МК.

35. * В треугольнике АВС: 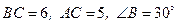. Найти площадь треугольника, если расстояние от вершины А до прямой ВС меньше .

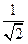36. * В равнобедренном треугольнике АВС 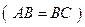медиана AD и биссектриса СЕ взаимно перпендикулярны. Найти .

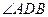37. В треугольнике АВС: 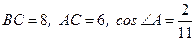. Найти .

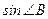38. В треугольнике АВС: 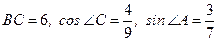. Найти АВ.

39. * В треугольнике АВС величина угла АВС относится к величине угла АСВ как 1:3. Биссектриса угла ВАС делит площадь треугольника в отношении 2:1. Найти величины углов треугольника АВС.

40. Точка на гипотенузе, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 и 40. Найти катеты треугольника.

41. Один из катетов прямоугольного треугольника равен b, а радиус описанного около этого треугольника окружности равен R. Найти длину биссектрисы угла, заключенного между данным катетом и гипотенузой.

42. В треугольнике АВС 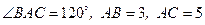. Найти длину биссектрисы BD и отрезков AD и CD.

43. В треугольнике АВС проведена биссектриса ВЕ, которую центр О вписанной окружности делит в отношении 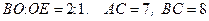. Найти АВ.

44. В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5. Определить площадь треугольника.

45. Дан треугольник со сторонами 12, 15 и 18. Проведена окружность, касающаяся обеих меньших сторон и имеющая центр на большей стороне. Найти отрезки, на которые центр окружности делит большую сторону треугольника.

46. Медиана, проведенная к гипотенузе прямоугольного треугольника, делит прямой угол в отношении 1:2 и равна 8. Найти меньший катет треугольника.

47. 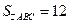. Из вершины тупого угла В проведена медиана BD длиной 3. 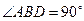. Найти АС.

48. В треугольнике АВС медиана 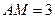перпендикулярна медиане 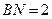. Найти площадь треугольника АВС.

49. Две стороны треугольника равны соответственно 6 и 8. Медианы, опущенные на эти стороны, взаимно перпендикулярны. Найти третью сторону треугольника.

50. Стороны треугольника равны 6 и 8. Медианы, проведенные к этим сторонам, перпендикулярны. Найти площадь треугольника.

51. Точка М – середина стороны АС треугольника АВС. Известно, что 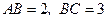, 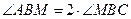. Найти .

52. * Найти площадь треугольника, если две его стороны равны 1 и 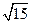, а медиана третьей стороны равна 2.

53. * В треугольнике АВС из вершины В проведена медиана и высота. Они делят угол АВС на три равные части. Найти углы треугольника АВС.

54. * Точка пересечения медиан прямоугольного треугольника удалена от катетов на расстояния 6 и 8. Найти расстояние от этой точки до гипотенузы.

55. ** В треугольнике АВС медиана AD и биссектриса ВЕ перпендикулярны и пересекаются в точке F. Найти площадь треугольника АВС, если площадь треугольника DEF равна 5.

56. ** Медианы треугольника равны 3, 4, 5. Найти площадь треугольника.

57. Найти радиус окружности, описанной около прямоугольного треугольника, если радиус окружности, вписанной в треугольник, равен 3, а меньший катет равен 10.

58. Найти периметр прямоугольного треугольника, если радиус описанной около него окружности равен 5, а радиус вписанной окружности равен 2.

59. Гипотенуза прямоугольного треугольника равна 10, а радиус вписанной окружности равен 2. Найти площадь этого треугольника.

60. В треугольнике АВС с углам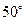и и 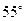вписана окружность с центром О. Наименьший из углов АОВ, ВОС, АОС равен…

61. В прямоугольном треугольнике высота, опущенная из вершины прямого угла, делит гипотенузу на отрезки 9 и 16, Найти радиус вписанной в треугольник окружности.

62. Точка касания вписанной в прямоугольный треугольник окружности делит один из катетов на отрезки длиной 2 и 4. Найти гипотенузу этого треугольника.

63. Радиус вписанной в треугольник окружности равен 2, а одна из точек касания делит сторону на отрезки 3 и 4. Найти площадь треугольника.

64. Площадь вписанного в прямоугольный треугольник круга равна 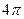, а гипотенуза в точке касания делится на отрезки длиной 3 и 10. Найти площадь треугольника.

65. В треугольнике АВС со сторонами 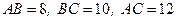вписана окружность, которая касается сторон треугольника в точках М, N, Р соответственно. Наименьшее из расстояний АМ, BN, СР равно…

66. В равнобедренном треугольнике АВС с основанием АС боковая сторона равна 60. Найти основание треугольника, если центр вписанной окружности делит высоту BD в отношении 12:5.

67. По данной стороне правильного треугольника, описанного около окружности, вычислить сторону правильного треугольника, вписанного в эту окружность.

68. В окружность вписан правильный треугольник, площадь которого равна 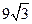, и в треугольник вписана окружность. Найти площадь получившегося кольца.

69. Стороны треугольника равны 35, 29 и 8. Найти радиус окружности, описанной около треугольника.

70. BD – высота треугольника АВС. Точка Е – середина ВС. 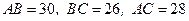. Найти радиус круга, описанного около треугольника BDE.

71. В окружность радиуса 6 вписан треугольник, две стороны которого равны 9 и 4. Найти высоту треугольника, опущенную на третью сторону.

72. Угол при вершине равнобедренного треугольника равен , а боковая сторона равна 8. Найти диаметр описанной около треугольника окружности.

73. В равнобедренном треугольнике отношение высоты к основанию равно 30. Основание относится к боковой стороне как 4:3. Найдите радиус вписанной окружности.

74. В равнобедренном треугольнике боковая сторона в 1,5 раза больше радиуса описанной около треугольника окружности. Найти угол при основании треугольника.

75. В равнобедренном треугольнике, две стороны которого равны 20 и 48, к боковой стороне проведена высота, и около полученных треугольников описаны окружности. Найдите расстояние между их центрами.

76. * Угол при основании равнобедренного треугольника равен 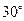. Найти отношение площади круга, описанного около этого треугольника, к площади вписанного в него круга.

77. * В равнобедренном треугольнике основание равно 16, а боковая сторона равна 10. Вычислить радиусы вписанной и описанной окружностей и расстояние между их центрами.

78. * Точка N лежит на стороне АС правильного треугольника АВС. Найти квадрат отношения радиусов окружностей, описанных около треугольников ABN и АВС соответственно, если .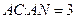

79. * Радиус вписанной в треугольник окружности равен 2, а одна из точек касания делит сторону на отрезки длиной 3 и 4. Найти площадь треугольника.

80. * Найти углы прямоугольного треугольника, если радиус описанного около него круга относится к радиусу вписанного круга как 5:2.

81. ** В треугольнике АВС на сторонах АВ и ВС взяты точки D и Е соответственно, причем 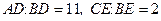. Найти отношение радиуса окружности, описанной около треугольника АВС к радиусу окружности, вписанной в этот треугольник, если известно, что , а .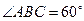

82. ** В треугольнике АВС через вершины А и С проведена окружность, пересекающая стороны АВ и ВС в точках D и Е соответственно. Известно, что 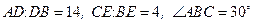. Найти отношение радиуса описанной около треугольника АВС окружности к радиусу вписанной в него окружности.

83. ** В прямоугольный треугольник АВС 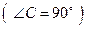площадью 30 вписана окружность с центром в точке О. 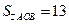. Найти стороны треугольника АВС.

84. ** В треугольнике АВС со сторонами 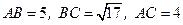на стороне АС взята точка М так, что 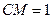. Найти расстояние между центрами окружностей. описанных около треугольников АВМ и ВСМ.

85. ** В треугольник с периметром 20 вписана окружность. Отрезок касательной, проведенной к окружности параллельно основанию, заключенный между сторонами треугольника, равен 2,4. Найти основание треугольника.

86. *** Из вершин А и С остроугольного треугольника АВС проведены высоты AN и СМ. Вычислить радиус окружности, описанной около треугольника АВС, если .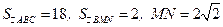

87. Длины сторон треугольника относятся как 3:4:6. Соединив середины его сторон, получим треугольник с периметром 3,9. Найти длину большей стороны исходного треугольника.

88. Сходственные стороны подобных треугольников равны 2 и 5. Площадь первого треугольника равна 8. Найти площадь второго треугольника.

89. Периметры подобных треугольников относятся как 2:3, а сумма их площадей равна 390. Найти площадь меньшего треугольника.

90. Высота треугольника равна 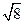. Прямая, параллельная основанию, отсекла от него треугольник, площадь которого в 2 раза меньше площади данного. Найти высоту меньшего треугольника.

91. Сторона треугольника равна 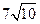. Параллельно ей проведена прямая. Отношение площадей отсеченного треугольника и трапеции равно 2:3. Найдите длину отрезка этой прямой внутри треугольника.

92. В треугольник с основанием 2 и высотой, проведенной к основанию, равной 3, вписан квадрат так, что две его вершины лежат на основании, а две другие – на боковых сторонах. Чему равна часть площади треугольника, не накрытая квадратом?

93. В прямоугольный треугольник с катетами а и b вписан квадрат, имеющий с треугольником общий прямой угол. Найти периметр квадрата.

94. Треугольник, основание которого равно 10, а площадь равна 60, разделен на 4 равные по площади части тремя отрезками, параллельными основанию. Найти расстояние от вершины треугольника до отрезка меньшей длины.

95. В равнобедренном треугольнике 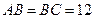. Через середину высоты BD проведен отрезок МР параллельно ВС. Найти длину МР.

96. Основание равнобедренного треугольника равно 12, а боковая сторона равна 18. К боковым сторонам проведены высоты. Найти длину отрезка, соединяющего основания высот.

97. В равнобедренном треугольнике АВС основание АС равно 18, а боковая сторона равна 15. На стороне АВ взята точка К, а на ВС – точка М так, что 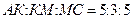. Найти площадь четырехугольника АКМС.

98. * Высота треугольника равна 4; она делит основание на две части, относящиеся как 1:8. Найти длину отрезка прямой, параллельной высоте и делящей треугольник на две равновеликие части.

99. * В прямоугольном треугольнике АВС из вершины С прямого угла проведена высота СD. Радиусы окружностей, вписанных в треугольники АСD и ВСD, равны соответственно 5 и 12. Найти радиус окружности. вписанной в треугольник АВС.

100. ** В треугольнике АВС на стороне АС взята точка М такая, что 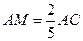, а на стороне ВС – точка К такая, что 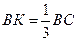. В каком отношении отрезок ВМ делит отрезок АК ?

101. Стороны треугольника АВС равны 120, 140 и 180. Найти высоту, проведенную к меньшей стороне.

102. В равнобедренном треугольнике основание равно 8, боковая сторона равна 5. Найти высоту, опущенную на боковую сторону.

103. В треугольнике высота, основание и сумма боковых сторон соответственно равны 12, 14 и 28. Найти синус угла при вершине треугольника.

104. В треугольнике АВС проведена высота ВК. Найти площадь треугольника АВК, есл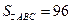и и .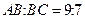

105. Дан треугольник АВС, в котором 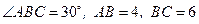. Биссектриса угла АВС пересекает сторону АС в точке D. Найти площадь треугольника АВD.

106. Точка 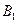лежит на стороне АС треугольника АВС, причем 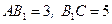. Точка О, лежащая на отрезке 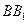, такова, что площадь треугольника СОВ равна 25. Найти площадь треугольника АОВ.

107. В треугольнике АВС точка D лежит на стороне АС, а точка Е – на стороне АВ. Известно, что и 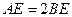. Найти отношение площадей треугольников BDE и АВС.

108. * В треугольнике АВС проведена медиана ВМ. Через ее середину О проведена прямая АО, пересекающая сторону ВС в точке N. Найти отношение .

109. ** В равнобедренном треугольнике АВС через вершины основания В, С и точку N, которая является серединой высоты, проведенной к основанию, проведены прямые CD и ВЕ 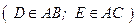. Определите площадь треугольника CED, если площадь треугольника АВС равна 27.

110. ** Стороны АВ, ВС и АС треугольника АВС относятся как 2:3:4. Точка О лежит вне треугольника между продолжениями сторон АВ и ВС за вершины А и С. Найти периметр треугольника, если расстояния от точки О до сторон АВ, ВС и АС равны соответственно и .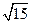

111. * Дан треугольник АВС, углы В и С которого относятся как 1:3, а биссектриса угла А делит площадь треугольника в отношении 2:1. Найти углы треугольника.