Самостоятельная работа «Вписанные и центральные углы»

Самостоятельная работа «Вписанные и центральные углы»

Выберите вариант ответа (задания 1-8)

1. Угол, вершина которого лежит в центре окружности называется

А) центральным; Б) вписанным; В) описанным.

2. Угол, вершина которого лежит на окружности называется

А) центральным; Б) вписанным; В) описанным.

3. Вписанный угол равен

А) двойной величине дуги, на которую он опирается;

Б) дуге, на которую он опирается;

В) половине дуги на которую он опирается.

4. Центральный угол равен

А) двойной величине дуги, на которую он опирается;

Б) дуге, на которую он опирается;

В) половине дуги, на которую он опирается.

5. Чему равен вписанный угол, опирающийся на дугу в 120⁰

А) 120⁰; Б) 60⁰; В) 240⁰

6. Чему равен центральный угол, опирающийся на дугу в 40⁰

А) 80⁰; Б) 20⁰; В) 40⁰

7. Чему равен вписанный угол, опирающийся на дугу в 100⁰

А) 50⁰; Б) 100⁰; В) 200⁰.

8.Чему равен центральный угол, опирающийся на дугу в 80⁰

А) 160⁰; Б) 80⁰; В) 40⁰.

Запишите ответ (задания 9-12):

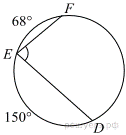
9. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.

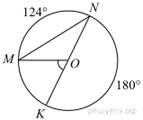
10. Найдите ∠KOM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°. Точка O — центр окружности.

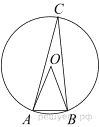
11. Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.

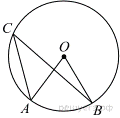
12. Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах).

Запишите решение (задания 13,14):

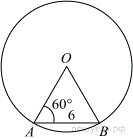
13. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.

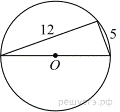
14. Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?