Треугольники. Четырехугольники

Элементарная математика Практикум по решению задач (планиметрия)

Треугольники. Четырехугольники

1. Катеты ВС и АС прямоугольного ∆АВС продолжены за вершину прямого угла. На продолжении катета ВС отложена точка D так, что СD= АС, а на продолжении катета АС отложена точка Е так, что СЕ=ВС. Доказать, что медиана СМ ∆АВС перпендикулярна отрезку DE.

2. Выразить сторону АС ∆АВС через медианы m_a_,m_b, m_c.

3. Доказать: длина медианы выражается формулой m_a= 0,5 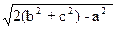_,где a, b, c – длины сторон треугольника.

4. Доказать, что в прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой, проведенными из той же вершины.

5. Основания трапеции – а и b. Найти длину отрезка, соединяющего середины диагоналей.

6. Внутри прямого угла дана точка М, расстояние которой от сторон угла равны 6 см и 8 см. Прямая, проходящая через точку М, отсекает от прямого угла треугольник площадью 100 см². Найти стороны этого треугольника.

7. В трапеции АВСD AD || BC (BC<AD). Биссектриса угла ВАD пересекает боковую сторону трапеции СD в точке Е. Найдите площадь трапеции, если известно, что СЕ:ЕD=1:3, СD_┴АD, ВС=6 см, АВ=10 см.

8. В прямоугольном треугольнике проведена биссектриса острого угла; отрезок, соединяющий ее основание с точкой пересечения медиан, перпендикулярен катету. Найти углы треугольника.

9. В треугольнике АВС известно, что ВС=12 см, АС=8 см и угол А вдвое больше угла В. Найти АВ.