- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ФОРМУЛ
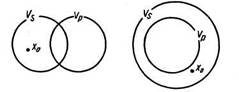
Рис. 6
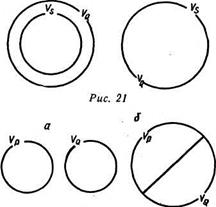
На каждой из этих диаграмм заключение верно, так как объемы понятий S и не-Р имеют общие элементы, например х0. Значит, следование правильное.
Пример 7. Выполняются ли следования:
(а) 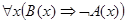 ├
├ 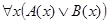
(б) 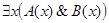 ├
├ 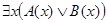 ?
?
Для случая категорических посылок отношения между их терминами исследованы, и мы, пользуясь этим, сразу рисуем ту диаграмму, на которой рассматриваемая посылка истинна. Если же посылка не категорическая, то отношение между ее компонентами требуется еще установить.
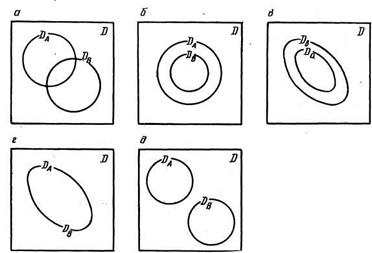
(а) Хотя посылка рассматриваемого следования категорическая, тем не менее на ее примере мы покажем установление отношения между компонентами посылки 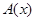 и
и 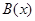 . Для этого вначале изобразим диаграммами Венна все возможные отношения между областями истинности логических функций, характеризующих
. Для этого вначале изобразим диаграммами Венна все возможные отношения между областями истинности логических функций, характеризующих 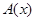 и
и 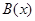 (рис. 7, а—д). Затем на каждой диаграмме покажем штриховкой область истинности логической функции, характеризующей формулу
(рис. 7, а—д). Затем на каждой диаграмме покажем штриховкой область истинности логической функции, характеризующей формулу 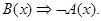
После этого отыщем те диаграммы, на которых посылка оказывается истинной. Для данной посылки, имеющей структуру 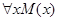 , где
, где 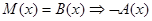 ,- это диаграмма, представленная на рис. 8, д. На диаграммах рис. 18, а—г посылка
,- это диаграмма, представленная на рис. 8, д. На диаграммах рис. 18, а—г посылка 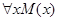 ложна, так как имеется
ложна, так как имеется  , не принадлежащий области истинности
, не принадлежащий области истинности 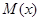 . На диаграмме рис. 8, д таких х нет.
. На диаграмме рис. 8, д таких х нет.
|
|
|
Итак, посылка следования (а) имеет значение И только на диаграмме, изображенной на рис. 8, д. Поэтому, в силу определения логического следования, решение вопроса о том, истинно ли заключение  на диаграммах, представленных на рис. 8, а—г, не требуется. Остается выяснить вопрос только для диаграммы на рис. 8, д. Область же истинности логической функции, связанной с предикатом
на диаграммах, представленных на рис. 8, а—г, не требуется. Остается выяснить вопрос только для диаграммы на рис. 8, д. Область же истинности логической функции, связанной с предикатом 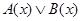 и изображенной на диаграмме рис. 7, д, можно представить в виде рис. 9.
и изображенной на диаграмме рис. 7, д, можно представить в виде рис. 9.
Исходя из рис. 9 и учитывая определение квантора общности, делаем вывод о ложности заключения 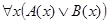 .
.
Значит, следование неверное.
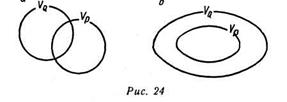
(б) Область истинности логической функции, связанной с формулой 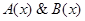 , при всех возможных отношениях между DA и DB изображена на рис. 10, а—д.
, при всех возможных отношениях между DA и DB изображена на рис. 10, а—д.
Посылка 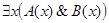 истинна на диаграммах рис. 10, а-г. На всех этих диаграммах истинно и заключение
истинна на диаграммах рис. 10, а-г. На всех этих диаграммах истинно и заключение 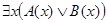 . Значит, следование правильное.
. Значит, следование правильное.
Пример 8. Верно ли, что
(а) 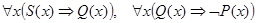 ├
├ 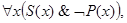
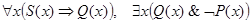 ├
├ 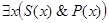 ?
?
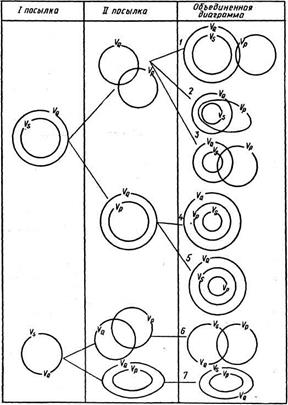
Вопрос о правильности следования решаем методом диаграмм Венна, учитывая при этом категоричность посылок и заключения. Этот метод для случая с двумя посылками состоит в следующем.
Изображаем все возможные отношения между объемами понятий S и Q первой посылки, затем - все возможные отношения между объемами понятий Q и Р второй посылки. После этого изображаем все возможные диаграммы, связывающие каждый случай для первой посылки с каждым случаем для второй посылки. При этом, конструируя объединенные диаграммы, следует учитывать все возможные отношения между VS и VР.
Если на каждой из полученных объединенных диаграмм заключение оказывается истинным, то следование правильно. Если же хотя бы на одной объединенной диаграмме заключение ложно, то следование неправильно.
(а) Так как первая посылка 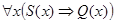 - общеутвердительное суждение, то ей соответствуют диаграммы, изображенные на рис. 11, а—б.
- общеутвердительное суждение, то ей соответствуют диаграммы, изображенные на рис. 11, а—б.
Так как вторая посылка 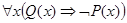 - общеотрицательное суждение, то ей соответствуют диаграммы на рис. 12, а—б.
- общеотрицательное суждение, то ей соответствуют диаграммы на рис. 12, а—б.
Для получения объединенных диаграмм комбинируем каждую диаграмму рис. 11, а, б с каждой диаграммой рис. 12, а, б. Получаем рис. 13.
На каждой из объединенных диаграмм (рис. 13) заключение 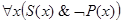 верно, так как объемы понятий S и не-Р имеют общие элементы.
верно, так как объемы понятий S и не-Р имеют общие элементы.
Значит, следование правильное.
|
|
|
|
(б) Первая посылка та же, что и в случае (а). Так как вторая посылка 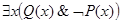 является частноотрицательным суждением, то ей соответствуют диаграммы на рис. 14, а-б Комбинируя диаграммы на рис. 11 и 14, получаем рис. 15.
является частноотрицательным суждением, то ей соответствуют диаграммы на рис. 14, а-б Комбинируя диаграммы на рис. 11 и 14, получаем рис. 15.
На первой объединенной диаграмме (рис. 15) заключение 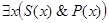 неверно, так как объемы понятий S и Р не имеют ни одного общего элемента.
неверно, так как объемы понятий S и Р не имеют ни одного общего элемента.
Значит, следование неправильное.
3.16. Сделайте заключение о связи между S и Р в следующих случаях.
(1) Любое S есть Q и любое Q есть Р.
(2) Любое S есть Q и никакое Q не есть Р.
(3) Любое S есть Q и некоторое Q есть Р.
(4) Любое S есть Q и некоторое Q не есть Р.
(5) Никакое S не есть Q и любое Q есть Р.
(6) Никакое S не есть Q и никакое Q не есть Р.
(7) Никакое S не есть Q и некоторое Q есть Р.
(8) Никакое S не есть Q и некоторое Q не есть Р.
(9) Некоторое S есть Q и любое Q есть Р.
(10) Некоторое S есть Q и никакое Q не есть Р.
(11) Некоторое S есть Q и некоторое Q есть Р.
(12) Некоторое S есть Q и некоторое Q не есть Р.
(1З) Некоторое S не есть Q и любое Q есть Р.
(14) Некоторое S не есть Q и никакое Q не есть Р.
(15) Некоторое S не есть Q и некоторое Q есть Р.
(16) Некоторое S не есть Q и некоторое Q не есть Р.
3.17. Какие из перечисленных ниже предложений следуют из х2 — 2х = 0?
1) x = 0 4) x = 0 Ù x - 2 = 0
2) x - 2 = 0 5) х2 — 2х = 0 Ú x - 3 = 0
3) x = 0 Ú x - 2 = 0 6) (х2 — 2х)(x - 3) = 0
3.18. Задайте предметную область D так, чтобы на этой области второй предикат был бы следствием первого:
а) «х кратно 3», «х - четно»
б) «х - квадрат», «х - ромб»
РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ФОРМУЛ
3.19. Докажите, что формулы алгебры предикатов F и Н равносильны тогда и только тогда, когда формула F Û Н является тавтологией.
3.20. Докажите, что справедливы следующие равносильности (формула Н не содержит х свободно):
a) 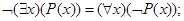
б) 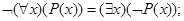
в) 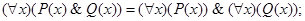
г) 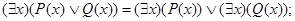
д) 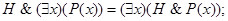
е) 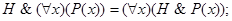
ж) 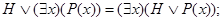
з) 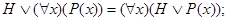
и) 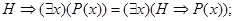
к) 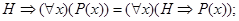
л) 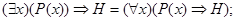
м) 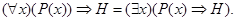
3.21. Для следующих формул алгебры предикатов найдите равносильную им приведенную форму, т. е. такую форму, в которой из операций алгебры высказываний имеются только операции , & и Ú, а знаки отрицания относятся только к предикатным переменным и к высказываниям:
а) 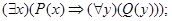
б) 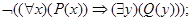
в) 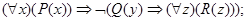
г) 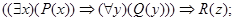
д) 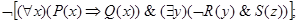
е) 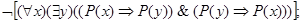
ж) 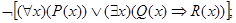
з) 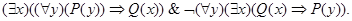
Решение. ж) Используя равносильности алгебры высказываний (см. задачу 1.42) и алгебры предикатов (см. предыдущую задачу), преобразуем равносильным образом эту формулу:
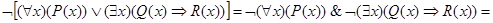
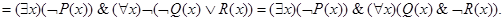
3.22. Применяя равносильные преобразования, приведите следующие формулы к предваренной (префексной) нормальной форме, т. е. к форме вида (Q1x1) ... (Qmxm) (F (x1, ..., хn)), где m £ n, каждый Qi есть один из кванторов " или $ и формула F (x1, ..., хn) не содержит кванторов:
а) 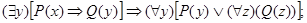
б) 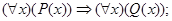
в) 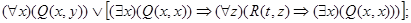
г) 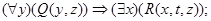
д) 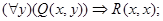
е) 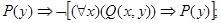
ж) 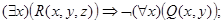
з) 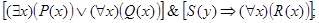
и) 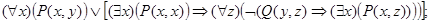
к) 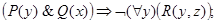
л) 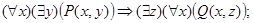
м) 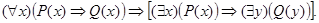
Решение. а) Читателю предлагается обосновать каждый шаг следующих равносильных преобразований, указав используемые равносильности:
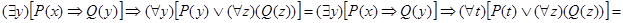
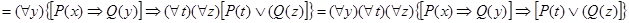
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|