Аффинные преобразования

Аффинные преобразования

Аффинная геометрия допускает изменение углов, но параллельные прямые остаются параллельными.

Геометрия Евклида – частный случай аффинной геометрии. Она допускает преобразования движения (перенос, вращение) и одинаковое масштабирование по осям. Углы не изменяются.

Выше были выведены уравнения для поворота плоскости. Добавим к повороту еще и перемещение. Получим уравнения преобразование движения.

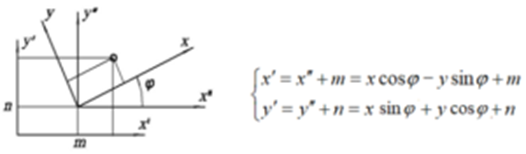
В матричном представлении уравнения запишутся так:

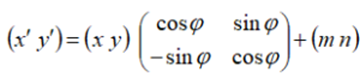
Обобщим уравнения преобразований движения к уравнениям аффинного преобразования плоскости:

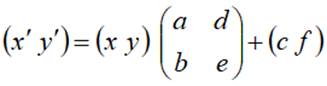
Принципиальное отличие уравнений преобразований движения от уравнений аффинного преобразования в том, что коэффициенты аффинного преобразования a, b, d и e независимы, т.е. они не связаны между собой тригонометрическими соотношениями.

Коэффициенты a и e определяют также и масштабирование по осям:

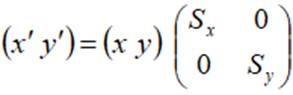
На рисунке показан треугольник, масштабированный с коэффициентами 0,5 по оси абсцисс и коэффициентом 2 вдоль оси ординат.

При отрицательных значениях коэффициентов сжатия/растяжения происходит отражение относительно соответствующих осей.