РЕШЕНИЕ УРАВНЕНИЙ

РЕШЕНИЕ УРАВНЕНИЙ

1. Основная задача

2. Принцип сжимающих отображений

3. Принцип неподвижной точки

4. Монотонные отображения

5. Задачи

Очень часто в математике под решением задачи подразумевается её сведение к другой задаче, которая представляется, по крайней мере, во многих случаях, проще, чем исходная. Задачи оптимизации часто сводятся к решению систем алгебраических уравнений (например, при использовании метода множите-лей Лагранжа). И хотя в примерах из учебников эти системы легко решаются, на самом деле решение систем уравнений – совсем не простое дело (вообще говоря, не более простое, чем сама задача непре-рывной оптимизации). Однако известны общие принципы, которые позволяют говорить о существова-нии решений и в ряде случаев - находить их. Изложению этих общих принципов и следствий из них и посвящён данный раздел.

1. Основная задача. Пусть некоторая система формально описывается векторной функцией от вектор-ного аргумента:

y = F(x), xÎRⁿ, yÎR^m, n ≥ 1, m ≥ 1,

или, в скалярной записи,

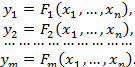
Основная проблема представляется в этом случае в виде задачи решения системы уравнений относи-тельно неизвестных x₁,…, x_n:

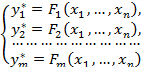(1)

или, в векторном виде,

y^*₌F(x), xÎRⁿ, y*ÎR^m, n ≥ 1, m ≥ 1. (2)

где вектор y^*предполагается заданным.

Ограничимся случаем m = n. Положим

f_i ( 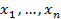) = 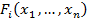- 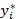(i = 1, ..., n). (3)

C учётом (3) (и того, что m = n) система (1) принимает вид

(4)

или, в векторном виде,

f(x) = 0. (5)

Известны несколько общих принципов, позволяющих делать утверждения относительно существования решений системы (5), их количества, а также позволяющих предложить процедуры поиска решений. Естественно, что ни один из них не является универсальным; все требуют каких-то предположений относительно функций f_i ( 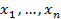) (i = 1, ..., n).

2. Принцип сжимающих отображений. Будем использовать понятие расстояния между точками в пространстве Rⁿ, положив

ρ(x, у) = 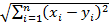. (6) (см. раздел «Топология евклидового пространства»). При n = 2 из формулы (6) получаем обычное рас-

стояние между точками плоскости.

Наряду с формулой (6) расстояние может быть задано формулами

ρ₁(x, у) = 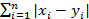; (6a)

ρ₂(x, у) = 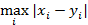; (6b)

ρ(x, у) = 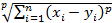(1 < p < ∞). (6c)

Способ задания расстояния не так важен; важно лишь, чтобы выполнялись условия:

ρ(x, x) = 0;

ρ(lx, lу) = |l| ρ(x, у);

ρ(x, z) + ρ(z, y) ≥ ρ(x, у) (неравенство треугольника).

Пусть f(x) - вектор-функция, т.е функция, отображающая пространство Rⁿ в себя. Это отображение называется сжимающим), если для всех x, уÎ Rⁿ

ρ(f(x), f(у)) ≤ α·ρ(x, у), (7)

где α - положительное число, меньшее единицы. Содержательно это понятие означает, что рассстояние ρ₂ между образами меньше, чем расстояние ρ₁между исходными точками (рис.1).

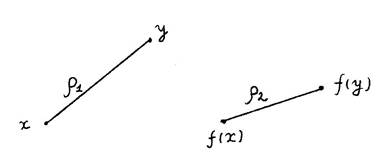
Рис.1

Принцип сжимащих отображений формулируется в виде следующего утверждения.

Утверждение 1. Если f(x) - сжимающее отображение пространства Rⁿ в себя, то уравнение

f(x) = x (8)

· всегда имеет решение;

· это решение (обозначим его через x*) единственно;

· оно может быть найдено как предел последовательности

x^k =f(x^k^-1) (k = 1, 2, ..., ), (9)

где начальная точка x⁰ - любая точка из Rⁿ.

Приведенное утверждение, конечно, не является аксиомой. Оно доказывается (доказательство не явля-ется сложным; оно здесь не приводится; стоит обратить внимание на то, что в нём существенно исполь-зуется свойство компактных множеств, рассмотренное в разделе «Топология евклидова пространства»: предел сходящейся последовательности точек компактного множества существует и принадлежит это-му множеству).

В большинстве случаев условие (7) выполняется не во всем пространстве, а только в некоторой его час-ти S (т.е. для x и у, принадлежащих некоторому множеству S). Если при этом все точки последователь-ности (9) лежат в S, то их предел является решением (8) (или, как еще говорят, неподвижной точкой отображения f). Суть этого названия связана с тем, что, как видно из (8), при отображении f эта точка никуда не перемещается.

Может возникнуть вопрос: ведь нам нужно решать уравнение (5) вида f(x) = 0, а принцип неподвижной точки, даже если он применим, позволяет найти только решение уравнения f(x) = x. Как же осуществить переход от одного вида к другому? Остановимся на этом подробнее. Пусть n = 1 и уравнение f(x) = 0 имеет корень x =α (его-то и надо найти!). Пусть ψ(x) - некоторая непрерывная в окрестности точки α функция и ψ(α) ≠ 0. Положим

φ(x) = x-ψ(x) f(x). (10)

Пусть f(α) = 0. Тогда

φ(α) = α - ψ(α) f(α) = α - ψ(α) · 0 = α, (11)

т.е. α является корнем уравнения

x = φ(x). (12)

Пусть, наоборот, α - корень уравнения (12). Тогда

α = φ(α) = α - ψ(α) f(α) или

0 = ψ(α) f(α)

и, так как ψ(α) ≠ 0, то, значит, f(α) = 0. Итак, уравнение

f(x) = 0 (13)

и уравнение (12) эквивалентны. Поэтому будем решать, вместо уравнения (13), уравнение (12), где φ(x) имеет вид (10). В то время как f(x) нам задана, выбор ψ(x) в наших руках (лишь бы было ψ(α) ≠ 0). Действительно, удается подобрать функцию ψ(x) так, что итерационный процесс (9), где f заменена на φ, является сходящимся. Два разных способа выбора ψ и дают метод секущих и метод Ньютона (касательных). Рассмотрим оба метода, ограничиваясь для простоты случаем n = 1.

1. Пусть при переходе через x =α функция f(x) меняет знак, а f '(x) и f ''(x) в некоторой окрестности точки x =α не меняют знака (говорят, что x =α - простой корень уравнения (13)). Пусть x* лежит в этой окрестности и при этом

f(x*)·f''(x*) > 0. (14)

Положим

ψ(x) = 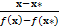. (15)

За начальное приближение x⁰ возьмем теперь любую точку, в которой f(x⁰) имеет знак, противоположный знаку f(x*). Далее итерации строятся в соответствии с (9) и с учетом (10) и (15). В результате простых выкладок получаем

xⁿ = (n = 1, 2, ..., ). (16)

Геометрическая интерпретация этого процесса, который и называется методом секущих, показана на рис.2 (в случае f '(x*) < 0, f ''(x*) > 0)

Рис.2

Имеет место

Утверждение 2. При x*,удовлетворяющем условию (14), и указанном выборе x⁰, достаточно близкого к α, последовательность {xⁿ}, определяемая формулой (16), сходится к корню α уравнения f(x) = 0.

Утвервдение 2 следует из того, что при данных условиях отображение (10) φ(x) = x-ψ(x) f(x) является сжимающим. Название метода представляется совершенно естественным с учетом рис.2.

2. Второй классический метод - метод Ньютона - получим, если положить в обшей формуле (10)

ψ(x) = 1/ f '(x). (17)

Соответствующий процесс (9) принимает вид

xⁿ = xⁿ^-1 - 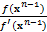. (18)

Начальное приближение x⁰ целесообразно также выбирать так, чтобы для него выполнялось (14). Геометрическая интерпретация метода Ньютона дана на рис.3 (случай f '(x⁰) > 0, f ''(x⁰) > 0).

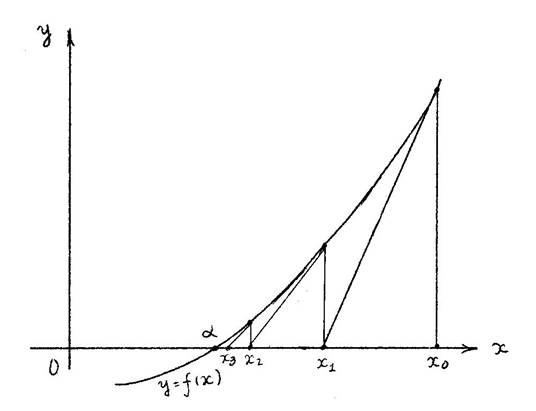
Рис.3

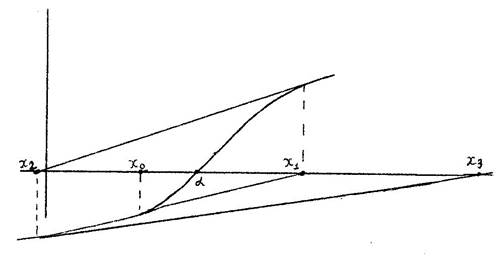
Рис.4

Существенность предположения о том, что в некоторой окрестности корня α вторая производная не должна менять знак, демонстрируется на рис.4 (здесь процесс расходится).

В заключение пункта рассмотрим многомерный вариант метода Ньютона. Положим

J(x) = (19)

и через J^-1(x) обозначим матрицу, обратную к J(x).

Имеет место

Утверждение 3. Если начальная точка x⁰была взята достаточно близко к решению (вектору) α системы

f(x) = 0,

то последовательные приближения

xⁿ = xⁿ^-1 - J^-1(xⁿ^-1) f(xⁿ^-1) (20)

сходятся к решению α.

При некоторых дополнительных условиях процедуру (20) можно заменить процедурой

xⁿ = xⁿ^-1 - J^-1(x⁰) f(xⁿ^-1),

которая гораздо проще, так как требует вычисления обратной матрицы J^-1(x) не на каждом шаге, а только один раз.

3. Принцип неподвижной точки. Общим недостатком описанных в пункте 2 методов является то, что они работоспособны только в некоторой окрестности решения (то же самое относится и к целому ряду гораздо более тонких методов). В конечном счёте они все основаны на замене исходной функции другой, у которой в окрестности неподвижной точки производная достаточно мала.

(Действительно, в силу хорошо известного равенства

f(b) - f(a) = f '(x) (b - a), (21)

где x - некоторая точка из интервала (a, b), малость производной позволяет сделать вывод о сжимающем характере (в соответствующей окрестности) отображения f (см. формулу (7)).

Во всех методах такого типа уже предполагается существование решения. Зная, что оно существует, но не зная, где именно, мы можем все же попробовать "угадать" начальную точку (привлекая, естественно, как это и следует делать в системном анализе, и всю нашу априорную информацию о системе). Если же мы ее «хорошо» угадаем (например, если мы просто знаем достаточно малую область, в которой должно быть решение), то применение указанных (или других) итерационных процедур действительно позволит найти решение.

Значительно сложнее обстоит дело как раз тогда, когда мы вообще не уверены в наличии решения. А чтобы его искать, хорошо бы сначала точно знать, что оно всё-таки есть. И здесь на помощь может прийти принцип неподвижной точки (точнее, целый ряд утверждений, известных под этим общим названием). Введем необходимые понятия.

Пусть W - ограниченная открытая область пространства Rⁿ (для простоты можно представлять себе круг на плоскости), а 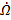- её граница (окружность). Пусть каждой точке xÎW сопоставлен вектор G(x) = (G₁(x), ..., G_n(x)). Функция G(x) на W называется векторным полем. Точку x, в которой G(x) = 0, назовём нулём векторного поля. Поле называется невырожденным на 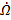, если оно не имеет нулей на 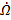, т.е. G(x) ≠ 0 для всех точек xÎ 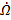. Далее рассматриваются только непрерывные поля (т.е. такие поля, у которых все функции G_i(x) (i = 1, ..., n) непрерывны), невырожденные на границе 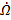рассматриваемой области W.

Одним из центральных понятий является понятие гомотопии двух векторных полей. Поля G¹(x) и G²(x) называются гомотопными, если существует непрерывная функция H(x, τ) (xÎ 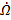, 0 ≤ τ ≤ 1), такая, что

H(x, 0) = G¹(x), H(x, 1) = G²(x) (22)

и при любом τÎ [0, 1] поле H(x, τ) невырожденно на 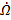. Функция H(x, τ) называется гомотопическим мостом между G¹(x) и G²(x).

Приведем одно простое, но чрезвычайно полезное утверждение относительно векторных полей.

Утверждение 4. Если в любой точке xÎ 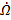векторы G¹(x) и G²(x) направлены непротивоположно, то поля G¹(x) и G²(x) гомотопны.

Доказательство. Рассмотрим функцию H(x, τ) = (1- τ)G¹(x) + τG²(x). Условие (22) очевидно выполняется, непрерывность H(x, τ) также очевидна. Если при каком-либо τÎ(0, 1) H(x, τ) = 0, то имеем

0 = (1- τ)G¹(x) + τG²(x),

или

G¹(x) = - 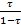G²(x), (23)

т.е. поля G¹(x) и G²(x) в этой точке направлены противоположно, что противоречит предположению. Утверждение доказано.

Следующим важным понятием является понятие вращения векторного поля. Каждому невырожденному на 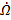непрерывному векторному полю G может быть сопоставлена целочисленная характеристика g(G, 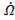), которая и называется вращением векторного поля G на 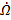. Мы не будем давать точного определения вращения. Остановимся только на некоторые важных свойствах вращений.

1. Гомотопные на 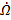поля имеют одинаковые вращения.

2. Пусть W = 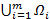, области W_j (j = 1, ..., m) попарно не пересекаются, векторное поле G определено и невырождено на 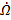, 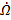₁, ..., 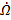_m. Тогда

g(G, 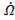) = 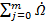_j.

3. Если векторное поле G определено и невырождено на W, то

g(G, 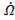) = 0.

Если в качестве W рассмотреть круг, то 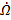- это окружность (рис.5). Вращение векторного поля G(x) на окружности - это число оборотов, которые делает вектор G(x) при полном прохождении точкой x окружности один раз (рис.5). С этим связано и само название. Вращение поля, показанного на рис.5, равно 2.

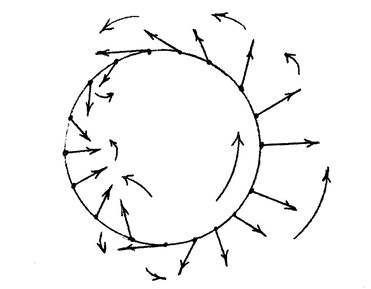
Рис.5

Нам будет нужно знать вращения некоторых простых полей.

4. Обозначим через Е поле G(x) = x. Если 0ÎW, то g(Е, ) = 1, g(-Е, ) = (-1)ⁿ. Если A - невырожденная матрица и поле A(x) = Ax, то g(A, ) = 1, если определитель A положителен, и -1, если он отрицателен. Если же 0ÏW, то g(Е, 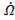) = g(-Е, 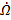) = g(A, 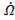) = 0.

А теперь уже все готово для того, чтобы выяснить, как же связаны решения уравнений вида

G(x) = 0 (24)

с вращением векторных полей. Дело в том, что векторную функцию G(x) = (G₁(x), G₂(x), ..., G_n(x)), представлящую собой левую часть системы (24), можно рассмотреть как векторное поле. Имеет место чрезвычайно сильное утверждение, которое является простой переформулировкой свойства 3.

Утверждение 5. Если g(G, 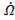) ≠ 0, то в области W существует точка x, в которой G(x) = 0.

Таким образом, всякое утверждение об отличии от нуля вращения векторного поля G(x) есть тем самым утверждение о наличии решения системы (24). Важно, что в случае, когда функция G(x) определена при всехxÎRⁿ, выбор области W целиком в наших руках. Целесообразно её выбирать так, чтобы для её границы 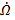выполнялось условие g(G, 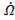) ≠ 0.

Продемонстрируем описанную схему для доказательства наиболее известного утверждения о неподвижной точке, известного под названием теоремы Брауэра.

Утверждение 6. Пусть непрерывная функция F отображает в себя замкнутый шар B. Тогда у отображения F существует неподвижная точка х*ÎB (т.е. F(х*) = х*).

Доказательство. Без ограничения общности можно считать центр шара расположенным в нуле (этого всегда можно достичь заменой системы координат).

Рассмотрим векторное поле G(x) = x - F(х). Его непрерывность следует из непрерывности F. Если это поле вырождено на границе шара B (т.е. на сфере S), то G(x) = 0 или x = F(х) и, следовательно, в этом случае утверждение доказано. Будем считать, что поле G(x) не вырождено на S. Установим гомотоп-ность полей G¹(x) = x и G²(x) = G(x) = x - F(х). Поскольку по условию любая точка xÎS переходит в точку шара В, то вектор x - F(х) не может быть противоположно направлен противоположно вектору x. Действительно, в противном случае

x - F(х) = -lx(l > 0)

или

F(х) = (1 + l)x. (25)

Но точка x принадлежит границе шара, и расстояние от точки (1 + l)x до нуля больше радиуса шара, т.е. F(х) Ï B, что противоречит условию. Гомотопность полей G¹(x) = x и G²(x) = x - F(х) следует теперь из утверждения 4. Но вращение поля G¹(x) = x на сфере S равно 0 в силу свойства вращений 4; в силу свойства вращений 1 получаем, что g(G², S) = 1, т.е. g(G², S) ) ≠ 0. В силу утверждения 5 для некоторой точки х шара B G²(x) = x - F(х) = 0 или x = F(х). Утверждение доказано.

Сразу заметим, что вместо шара можно рассмотреть любое другое множество, полученное из него непрерывной деформацией без разрывов (гомотопное шару). Однако окружность или кольцо, например, не гомотопны кругу, и для них теорема Брауэра неверна.

Вернемся к исходной задаче о разрешимости систем уравнений. Рассмотрим систему

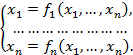(26)

Предположим, что все функции f₁, ..., f_n ограничены, т.е. | f_i (x) | < M для всех i = 1, ..., n, всех xÎRⁿ, и не-которого числа M. Рассмотрим шар радиуса 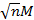c центром в нуле. Легко видеть, что при отображении f = (f₁, ..., f_n) любая точка из этого шара не выйдет из него. Поэтому существование решения системы (26) следует из теоремы Брауэра.

Приведем еще одно понятие. Поле G(x) на сфере S с центром в нуле называется нечётным, если в любых диаметрально противоположных точках сферы S поля направлены противоположно, т.е. G(x) = - G(-x).

Имеет место

Утверждение 7. Вращение нечетного поля нечетно.

С помощью утверждения 7 доказывается значительно более общий результат.

Утверждение 8. Пусть поле G(х) невырождено на сфере S и

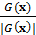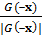≠ для всех хÎ S. (27)

Тогда вращение поля G(х) нечётно и, следовательно, существует точка хÎВ,в которой G(х) = 0.

Таким образом, некоторые из приведенных утверждений говорят о наличии решений у системы вида x= F(х), а другие - о наличии решений у системы вида G(х) = 0. Область применений этих утверждений можно расширить хотя бы за счет того что оба вида систем эквивалентны, как это уже объяснялось.

В заключение пункта заметим следующее. Пусть g(G, 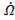) ≠ 0. Тогда можно гарантировать существова-ние нуля не только у векторного поля G(х), но и у поля G(х) + εQ(х), где Q(х) - любое другое непрерыв-ное поле, а ε достаточно мало. Следовательно, вывод о существовании решения уравнения G(х)=0 в данном случае «инвариантен» по отношению к малым деформациям G(х) (например, к малым ошибкам измерения, если значения G(х) получены из эксперимента).

4. Монотонные отображения. В этом пункте привлекается ещё несколько понятий, с помощью которых формулируются утверждения о разрешимости уравнений типа (4) или (26).

Во многих случаях по самому смыслу задачи переменные 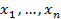не могут быть отрицательными. При этом функции f₁, ..., f_n также принимают неотрицательные значения. Такую векторную функцию (отображение) f = ( f₁, ..., f_n ) назовем положительной.

Введем следующий способ сравнения векторов х и у: будем писать, что у 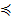х (у не превосходит х ), если y_i ≤ x_i (i = 1, ..., n). Ясно, что не любые два вектора сравнимы. Например, (5,6) 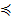(10,8), но векторы (5,10) и (8,6) не сравнимы (оба варианта у 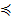х и х 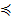у не имеют места). Отображение f назовём монотон-ным, если

у 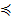х → f (у) 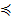f (х). (28)

Наконец, множестве всех точек хÎRⁿ, которые удовлетворяют условиям

v⁰ 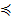х 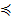w⁰, (29)

называется конусным отрезком с концами v⁰и w⁰. Геометрическая интерпретация конусного отрезка [v⁰,w⁰] приведена на рис.6.

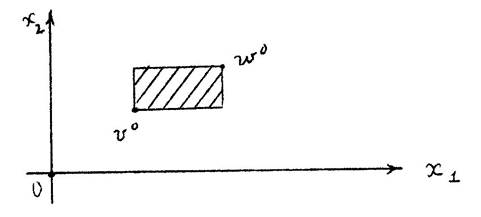
Рис.6

Теперь сформулируем принцип Бирхгофа-Тарского в виде следующего утверждения.

Утверждение 9. Всякое монотонное отображение f, переводящее в себя некоторый конусный отрезок [v⁰,w⁰], имеет по крайней мере одну неподвижную точку х*Î [v⁰, w⁰].

Удивительный характер этого утверждения состоит в том, что здесь, в отличие от всех предыдущих ут-верждений, не требуется непрерывности f. Отказ от непрерывности делает сразу же неверными все предыдущие принципы. Однако здесь за счёт монотонности все же можно гарантировать существова-ние неподвижной точки. Более того, в отличие от теоремы Брауэра, в которой не дается никакого алгоритма для поиска неподвижной точки, в данном случае при дополнительном предположении непрерывности f последовательность (9)

x^k =f(x^k^-1) (k = 1, 2, ..., ),

при начальной точке x⁰= v⁰ сходится к неподвижной точке отображения f.

Проиллюстрируем принцип Биркгофа-Тарского при n = 1. Из определений сразу следует, что у 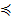х означает у ≤ х, т.е. что монотонное отображение - это просто монотонная функция, а конусный отрезок - зто обычный отрезок. Таким образом, если монотонная функция переводит отрезок [0, 1] в себя (т.е. f(0) ≥ 0, f(1) ≤ 1), то её график обязательно пересечется с графиком у = х (см. рис.7 ). То, что предположение о монотонности существенно, показывает рис.8.

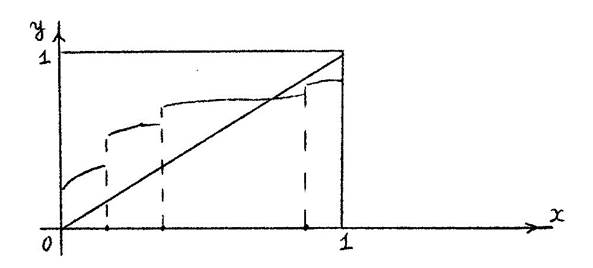
Рис.7

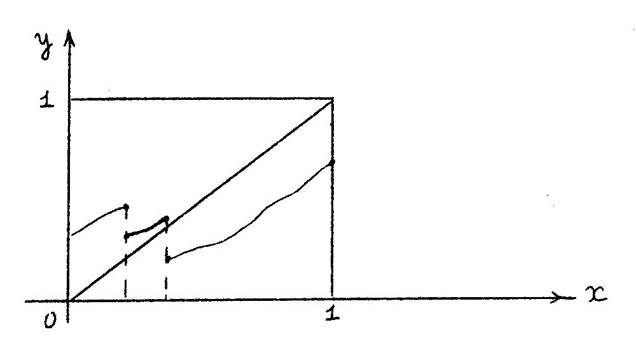
Рис.8

Приведем теперь некоторый более "технический" пример, являющийся аналогом известной модели межотраслевого баланса.

Пусть производство состоит из n отраслей (процессов, агрегатов и т.д.) и при этом производится n ви-дов продукции. Пусть i-ый агрегат выпускает i-ый продукт в количестве x_i и на выпуск единицы этого продукта расходуется a_ji единиц j-го продукта. Чистый выпуск i-го продукта при этом равен

y_i = x_i - 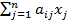(i = 1, ..., n). (30)

Но затраты могут быть и нелинейными, т.е. при производстве вектора хi-ый продукт в системе расходу-ется в количестве p_i( 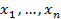) (i = 1, ..., n). Чистые выпуски при этом равны

y_i = x_i - p_i( 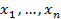) (i = 1, ..., n). (31)

Здесь возникают следующие вопросы. Увеличиваются ли чистые выпуски (а именно они важны) при увеличении х (т.е. при увеличении выпуска каждым отдельным агрегатом)? Что нужно делать, т.е. как менять компоненты х, чтобы увеличить чистые выпуски? и т.д.

Предположим, что затраты p(х) растут монотонно по х (т.е. чем больше производим, тем больше промежуточных продуктов нужно использовать ) и что p(0) = 0.

Пусть чистый выпуск продукции при некотором х⁰ равен у⁰, т.е. у⁰ = х⁰- p(х⁰). Тогда для любого набора у 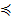у⁰ существует такой набор х, что

у = х- p(х). (32)

Для доказательства достаточно заменить, что монотонное отображение p(х) + упереводит в себя конусный отрезок [0, х⁰]. Действительно, p(0) + у 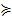0, p(х⁰) + у 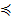х⁰, так как у 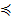у⁰. Неподвижная точка отображения является решением системы p(х) + у = х или у = х- p(х).

5. Задачи.

1. Доказать, что для расстояния, определяемого формулой (6), выполняется неравенство треугольника

2. Тот же вопрос для расстояния, определяемого формулой (6a)

3. Тот же вопрос для расстояния, определяемого формулой (6b)

4. Тот же вопрос для расстояния, определяемого формулой (6c)

5. Указать множество S на числовой прямой, на котором отображение f(x) = x³ является сжимающим

6. Указать множество S на числовой прямой, на котором отображение f(x) = x^0,2 является сжимающим

7. Указать множество S на числовой прямой, на котором отображение f(x) = ln(x^0,2) + 0,5x²является сжимающим

8. Доказать, что предел последовательности (9) единственен

9. Проверить, что при ψ(x), заданной формулой (15), последовательные приближения xⁿ определяются формулой (16).

10. Продемонстрировать на примере существенность условия (14) при выборе x*

11. Дать геометрическую интерпретацию метода секущих при всех сочетаниях знаков 1-й и 2-й производной.

12. Задача 6 для метода Ньютона

13. Задача 7 для метода Ньютона

14. Проверить, что при ψ(x), заданной формулой (17), последовательные приближения xⁿ определяются формулой (18).

15. Пусть в любой точке хÎ 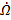|G¹(x)| > |G²(x)|. Доказать, что поля G¹(x) и G¹(x) + G²(x) гомотопны (см. утверждение 4)

16. Пусть 0ÎW и для любого xÎ 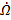|F(x) - x | < | F(x) | + | x |. Тогда уравнение F(x) = 0 разрешимо в W

17. Пусть 0ÎW и для любого xÎ 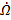можно указать такой номер j, что x_jF_j(x) > 0. Тогда уравнение F(x)=0 разрешимо в W

18. Доказать, что вращение g(G, 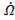) не меняется при изменении знака у чётного числа компонент G

19. Привести пример, иллюстрирующий, что теорема Брауэра неверна для окружности

20. Привести пример, иллюстрирующий существенность непрерывности F в теореме Брауэра

21. Доказать утверждение 8, исходя из утверждения 7

22. Доказать, что последовательность (9) при монотонном и непрерывном отображения f сходится к неподвижкой точке (при x⁰= v⁰)

23. Привести пример, когда при разрывном f последовательность (9) сходится к неподвижной точке f

24. Привести пример, когда при разрывном f последовательность (9) не сходится

25. Привести пример, когда при разрывном f последовательность (9) сходится к точке, не являющейся неподвижной точкой f