
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Повторение. СТЕПЕНИ И КОРНИ. Упражнения для самостоятельной работы. Тема ЛОГАРИФМЫ. Специальные обозначения
Повторение. СТЕПЕНИ И КОРНИ
Упражнения для самостоятельной работы
(выполнить на отдельных листах)
№1. Вычислить:
а) 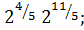 б)
б) 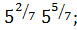 в)
в) 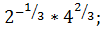 г)
г) 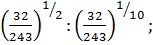
д) 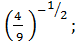 е)
е) 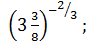 ж)
ж) 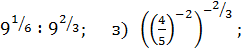 и)
и) 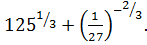
№2. Представить выражение в виде степени:
а) 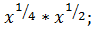 г)
г) 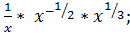 ж)
ж) 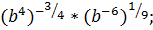
б) 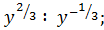 д)
д) 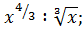 з)
з) 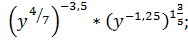
в) 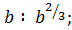 е)
е) 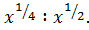
№3. Вычислить:
а) 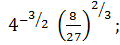 б)
б) 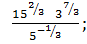 в)
в) 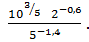
№4. Найти значения корней:
а) 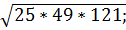 б)
б) 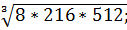 в)
в) 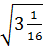 ; г)
; г) 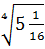 ; д)
; д) 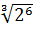 ; е)
; е) 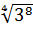 ; ж)
; ж) 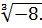
№5. Расположить числа в порядке
а) возрастания 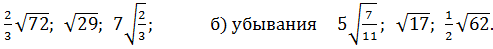
№6. Вывести из-под знака корня множители:
а) 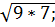 б)
б) 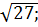 в)
в) 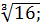 г)
г) 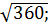
д) 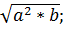 e)
e) 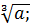 ж)
ж) 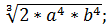 з)
з) 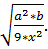
№7. Ввести под знак корня множители:
а) 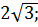 б)
б) 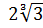 в) 2
в) 2 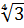 г) 2
г) 2 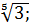
д) a 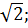 e)
e) 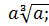 ж)
ж) 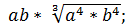 з) a b*
з) a b* 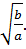
№8. Упростить следующие арифметические корни:
а) 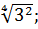 б)
б) 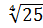 ; в)
; в) 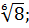 г)
г) 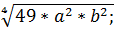 д)
д) 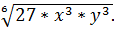
Тема ЛОГАРИФМЫ
Логарифмом положительного числа a (a > 0) по основанию b
(b >0, 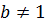 ) называют показатель степени, в которую надо возвести b, чтобы получить a.
) называют показатель степени, в которую надо возвести b, чтобы получить a.
Обозначение: 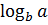 .
.
Примеры:
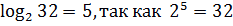 ;
;
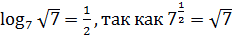 .
.
Специальные обозначения
Десятичный логарифм
log10 a = lg a
Натуральный логарифм
logea = lna(e ͌ 2,7182...)
Основное логарифмическое тождество:
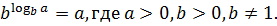
Примеры:
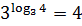 ;
;
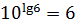 .
.
Свойства и формулы логарифмирования 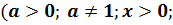
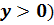 :
:
1) 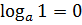 ;
;
2) 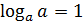 ;
;
3) Логарифм произведения положительных чисел равен сумме логарифмов множителей:
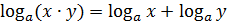
4) Логарифм частного положительных чисел равен разности логарифмов делимого и делителя:
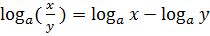
5) Логарифм степени положительного числа равен произведению показателя степени на логарифм основания этой степени
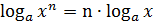
Обобщенные формулы логарифмирования:
1) 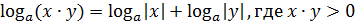 ;
;
2) 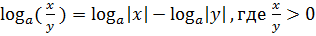 ;
;
3) 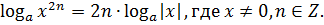
Формула перехода к логарифмам с другим основанием:
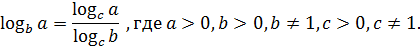
Следствия:
1) 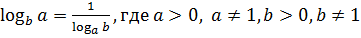 ;
;
2) 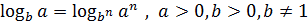 ;
;
3) 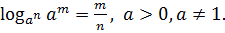
Пример 1. Найти значения выражений:
а) log6 270 − log6 7,5;
б) log5 775 − log5 6,2;
в) 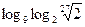 .
.
Решение. Первые два выражения преобразуются как разность логарифмов:
а) log6 270 − log6 7,5 = log6 (270 : 7,5) = log6 36 = log6 62 = 2;
б) log5 775 − log5 6,2 = log5 (775 : 6,2) = log5 125 = log5 53 = 3.
в) Для вычисления третьего выражения придется выделять степени — как в основании, так и в аргументе. Для начала найдем внутренний логарифм:
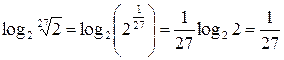 .
.
Затем — внешний:
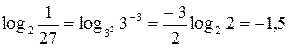 .
.
Ответ: а) 2; б) 3; в) −1,5.
ПРИМЕР 2. Найдите значение выражения:
а) 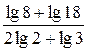 ;
;
б) 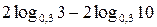 ;
;
в) 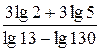 ;
;
г) 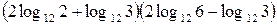 .
.
Решение:
а) 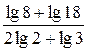
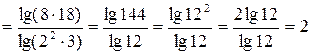 ;
;
б) 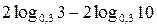
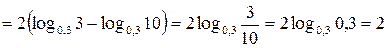 ;
;
в) 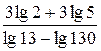
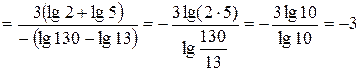 ;
;
г) 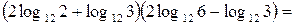
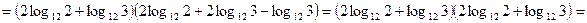
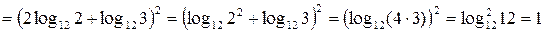 .
.
Ответ: 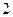 ;
; 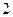 ;
; 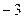 ;
; 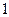 .
.
ПРИМЕР 3. Найдите 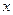 , если:
, если:
а) 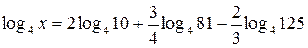 ;
;
б) 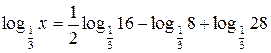 .
.
Решение:
а) 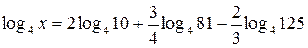 ;
;
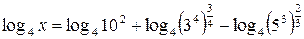 ;
;
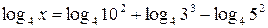 ;
;
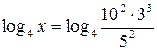
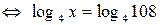
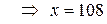 .
.
б) 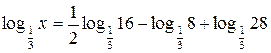 ;
;
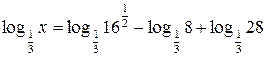 ;
;
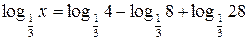 ;
;
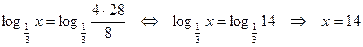 .
.
Ответ: 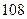 ;
; 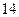 .
.
ПРИМЕР 4. Известно, что 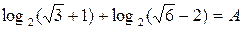 . Найти
. Найти 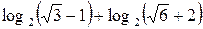 .
.
Решение:
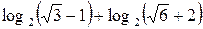
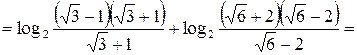
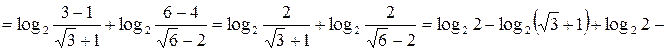
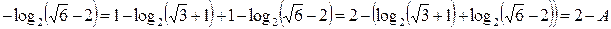 .
.
Ответ: 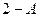 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|