
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Граничные условия.
Тема 6
Электростатическое поле
1. Основные уравнения электростатики
Электростатическое поле описывается системой дифференциальных уравнений,
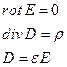
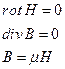
которая получается из системы уравнений Максвелла в предположении, что векторы поля не зависят от времени и отсутствует перемещение зарядов (j = 0). Аналогично находятся основные уравнения электростатики в интегральной форме:
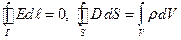 (2)
(2)
Электростатическое поле обладает рядом специфических свойств. В частности, непосредственно из уравнений Максвелла следует, что оно является потенциальным, а его векторные линии имеют истоки и стоки: они начинаются и заканчиваются на зарядах. В случае электростатического поля вектор Е можно представить в виде градиента скалярной функции и, называемой электростатическим потенциалом:
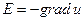 (3)
(3)
Соотношение (3) получается из формулы 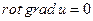 .
.
|

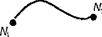 Выясним физический смысл электростатического потенциала. Вычислим работу
Выясним физический смысл электростатического потенциала. Вычислим работу 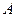 , совершаемую при перемещении точечного заряда величины
, совершаемую при перемещении точечного заряда величины 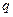 из точки
из точки 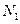 в точку
в точку 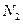 по контуру
по контуру 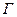 (рис.9). Так как напряженность
(рис.9). Так как напряженность 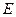 электрического поля определяется как сила, с которой поле действует на единичный точечный положительный заряд, то
электрического поля определяется как сила, с которой поле действует на единичный точечный положительный заряд, то
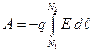 (4)
(4)
Знак минус в формуле (4) означает, что положительная работа совершается в том случае, когда заряд перемещается против сил поля. Подынтегральное выражение в формуле (4) можно представить в виде.
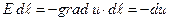 (5)
(5)
где 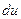 - полный дифференциал и. Второе равенство в формуле (5) представляет собой известное тождество векторного анализа. Для его доказательства достаточно
- полный дифференциал и. Второе равенство в формуле (5) представляет собой известное тождество векторного анализа. Для его доказательства достаточно 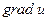 и
и 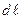 разложить по ортам декартовой системы координат
разложить по ортам декартовой системы координат 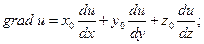
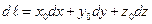 ) и вычислить скалярное произведение. Подставляя (5) в (4), получаем
) и вычислить скалярное произведение. Подставляя (5) в (4), получаем
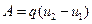 (6)
(6)
где 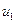 и
и 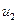 - значения потенциала и в точках
- значения потенциала и в точках 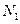 и
и 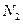 соответственно. Полагая
соответственно. Полагая 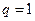 Кл, получаем, что работа, совершаемая при перемещении единичного точечного положительного заряда в электростатическом поле, численно равна разности потенциалов в конечной и начальной точках пути. Она не зависит от формы пути, по которому перемещается заряд, и от абсолютного значения потенциала. Если потенциалы бесконечно удаленных точек считать равными нулю, то потенциал и в точке N можно определить как работу, которую нужно совершить для перемещения единичного точечного положительного заряда из бесконечности в точку N. Потенциал измеряется в вольтах.
Кл, получаем, что работа, совершаемая при перемещении единичного точечного положительного заряда в электростатическом поле, численно равна разности потенциалов в конечной и начальной точках пути. Она не зависит от формы пути, по которому перемещается заряд, и от абсолютного значения потенциала. Если потенциалы бесконечно удаленных точек считать равными нулю, то потенциал и в точке N можно определить как работу, которую нужно совершить для перемещения единичного точечного положительного заряда из бесконечности в точку N. Потенциал измеряется в вольтах.
Находим связь между разностью потенциалов в точках 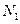 и
и 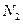 и напряженностью электростатического поля:
и напряженностью электростатического поля:
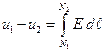 (7)
(7)
Если потенциалы бесконечно удаленных точек считаются равными нулю, то выражение (7) принимает вид
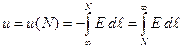
Было показано, что в случае однородных сред ( 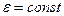 ) электростатический потенциал удовлетворяет уравнению Пуассона. Запишем в виде:
) электростатический потенциал удовлетворяет уравнению Пуассона. Запишем в виде:
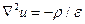 (8)
(8)
Если в рассматриваемой части пространства заряды отсутствуют ( 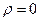 ), то (8) переходит в уравнение Лапласа
), то (8) переходит в уравнение Лапласа
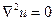 (9)
(9)
В тех случаях, когда заряды распределены в ограниченной области V с плотностью 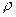 (
( 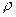 -функция координат), потенциал
-функция координат), потенциал 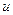 определяется выражением
определяется выражением
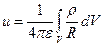 (10)
(10)
где R-расстояние от точки интегрирования 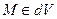 до точки наблюдения
до точки наблюдения 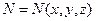 .
.
В случае поверхностных зарядов, распределенных с плотностью ps на поверхности S, нужно использовать формулу
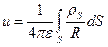 (11)
(11)
где R- расстояние от элемента dS до точки, в которой вычисляется потенциал.
Если поле создается заряженной нитью конечных размеров, т.е. зарядами, распределенными вдоль линии, то потенциал выражается формулой
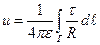 (12)
(12)
где интегрирование осуществляется вдоль нити (контур 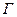 ); R- расстояние от элемента
); R- расстояние от элемента 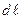 до точки, в которой вычисляется потенциал (рис.2.8), а
до точки, в которой вычисляется потенциал (рис.2.8), а 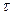 -линейная плотность заряда, определяемая выражением
-линейная плотность заряда, определяемая выражением
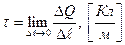 (13)
(13)
Записанные соотношения позволяют определить потенциал, а следовательно, и векторы электростатического поля в однородном изотропном пространстве по заданному распределению зарядов.
Чтобы получить наглядное представление об электростатическом поле, его изображают графически. При этом помимо силовых линий обычно рассматривают его эквипотенциальные поверхности, т.е. поверхности равного потенциала. Выясним связь между поверхностями равного потенциала и силовыми линиями электростатического поля. На эквипотенциальной поверхности потенциал 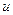 постоянен и, следовательно,
постоянен и, следовательно, 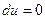 . При этом согласно соотношению (5) должно выполняться равенство
. При этом согласно соотношению (5) должно выполняться равенство 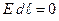 , где вектор
, где вектор 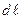 совпадает по направлению с касательной к эквипотенциальной поверхности. Это равенство означает, что поверхности равного потенциала и силовые линии электростатического поля пересекаются под прямым углом. Зная семейство эквипотенциальных поверхностей, можно построить силовые линии, и, наоборот, зная силовые линии, можно построить эквипотенциальные поверхности.
совпадает по направлению с касательной к эквипотенциальной поверхности. Это равенство означает, что поверхности равного потенциала и силовые линии электростатического поля пересекаются под прямым углом. Зная семейство эквипотенциальных поверхностей, можно построить силовые линии, и, наоборот, зная силовые линии, можно построить эквипотенциальные поверхности.
2. Граничные условия.
До сих пор рассматривалось электростатическое поле в однородном пространстве. Если имеются две (или более) разнородные среды, то для определения поля необходимо знать граничные условия для составляющих векторов Е и D и потенциала 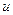 на границе раздела. Электростатическое поле является частным случаем электромагнитного поля. Поэтому граничные условия для векторов Е и D должны выполняться и для электростатического поля. Эти условия имеют вид:
на границе раздела. Электростатическое поле является частным случаем электромагнитного поля. Поэтому граничные условия для векторов Е и D должны выполняться и для электростатического поля. Эти условия имеют вид:
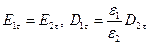 (14)
(14)
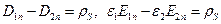 (15)
(15)
Так как при решении конкретных задач, как правило, оперируют с функцией 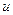 , то от условий для векторов Е и D нужно перейти к граничным условиям для потенциала
, то от условий для векторов Е и D нужно перейти к граничным условиям для потенциала 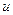 . Используя соотношение (3)
. Используя соотношение (3) 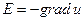 следующее равенство:
следующее равенство:
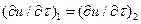 (16)
(16)
где оператор 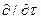 означает дифференцирование по любому направлению в плоскости, касательной к поверхности раздела в рассматриваемой точке. Интегрируя равенство (16) по
означает дифференцирование по любому направлению в плоскости, касательной к поверхности раздела в рассматриваемой точке. Интегрируя равенство (16) по 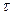 , получаем
, получаем
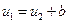 (17)
(17)
|
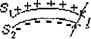
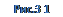 где
где 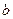 - произвольная постоянная, а
- произвольная постоянная, а 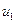 и
и 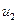 - значения потенциала и на поверхности раздела в первой и второй средах соответственно. Постоянную
- значения потенциала и на поверхности раздела в первой и второй средах соответственно. Постоянную 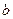 в большинстве случаев можно считать равной нулю. Действительно, потенциал и, созданный объемными или поверхностными зарядами, является непрерывной функцией. При этом из равенства (17) следует, что
в большинстве случаев можно считать равной нулю. Действительно, потенциал и, созданный объемными или поверхностными зарядами, является непрерывной функцией. При этом из равенства (17) следует, что
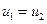 (18)
(18)
Соотношение (18) нарушается, если на поверхности раздела имеется двойной заряженный слой.
Переходя в формулах (3.14) 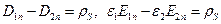 к функции и, получаем второе граничное условие для электростатического потенциала:
к функции и, получаем второе граничное условие для электростатического потенциала:
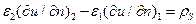 (19)
(19)
где оператор 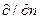 означает дифференцирование по нормали к поверхности раздела, направленной из второй среды в первую.
означает дифференцирование по нормали к поверхности раздела, направленной из второй среды в первую.
Если одна из сред является проводником, то граничные условия принимают более простой вид. В самом деле, при анализе макроскопических свойств поля проводник можно рассматривать как замкнутую область, внутри которой возможно свободное перемещение зарядов. Плотность потока зарядов, т.е. плотность тока проводимости в проводнике, пропорциональна напряженности электрического поля: 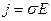 . В электростатике перемещение зарядов отсутствует:
. В электростатике перемещение зарядов отсутствует: 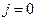 . Так как
. Так как 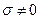 , то напряженность электростатического поля внутри проводника должна быть равна нулю. Это - одна из особенностей электростатического поля. Известно, что переменное электромагнитное поле не проникает в идеальный металл. Электростатическое поле равно нулю внутри любого реального проводника.
, то напряженность электростатического поля внутри проводника должна быть равна нулю. Это - одна из особенностей электростатического поля. Известно, что переменное электромагнитное поле не проникает в идеальный металл. Электростатическое поле равно нулю внутри любого реального проводника.
Внутри проводника grad и = 0. Откуда и = const. Следовательно, в электростатике все точки проводника имеют один и тот же потенциал. Это позволяет говорить о потенциале проводника. Потенциалы изолированных друг от друга проводников могут, конечно, иметь разные значения.
Найдем граничные условия на поверхности проводника для составляющих векторов Е и D. Пусть первая среда - диэлектрик, а вторая - проводник. Тогда, полагая 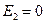 и
и 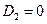 , получаем
, получаем
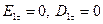 (20)
(20)
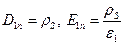 (21)
(21)
Условия (3.19) и (3.20) можно переписать в векторной форме:
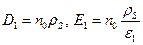 (22)
(22)
Подчеркнем, что в случае переменного поля аналогичные условия выполняются лишь на поверхности идеального проводника, а в электростатике условия (20)—(22) справедливы при любой отличной от нуля удельной проводимости второй среды.
Граничные условия для потенциала 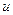 на поверхности проводника получаются из формул (20) и (21):
на поверхности проводника получаются из формул (20) и (21):
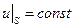 (23)
(23)
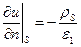 (24)
(24)
Нормаль 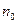 считается внешней по отношению к проводящей среде.
считается внешней по отношению к проводящей среде.
Из условия (23) следует, что поверхность проводника всегда эквипотенциальна.
3. Энергия электростатического поля.
Как известно из курса физики, энергия 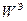 электростатического поля, сосредоточенного в объеме
электростатического поля, сосредоточенного в объеме 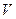 , определяется формулой (1.131)
, определяется формулой (1.131) 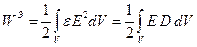 . Эту формулу можно преобразовать таким образом, чтобы энергия
. Эту формулу можно преобразовать таким образом, чтобы энергия 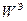 была выражена через заряды. Заменяя вектор Е через
была выражена через заряды. Заменяя вектор Е через 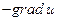 и используя тождество
и используя тождество 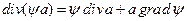 , где
, где 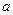 и
и 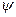 - произвольные векторная и скалярная функции, имеющие первые производные, получаем
- произвольные векторная и скалярная функции, имеющие первые производные, получаем
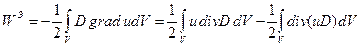 (25)
(25)
Последний интеграл в (25) преобразуем по теореме Остроградского-Гаусса:
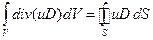 (26)
(26)
где 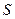 -поверхность, ограничивающая объем V.
-поверхность, ограничивающая объем V.
Предположим, что заряды, создающие электростатическое поле, сосредоточены в ограниченной области 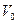 , и распространим интегрирование в формуле (26) на все пространство. Таким образом, интеграл (26) при
, и распространим интегрирование в формуле (26) на все пространство. Таким образом, интеграл (26) при 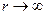 убывает как
убывает как 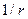 и в пределе равен нулю. Учитывая, что
и в пределе равен нулю. Учитывая, что 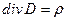 , получаем окончательное выражение для энергии электростатического поля:
, получаем окончательное выражение для энергии электростатического поля:
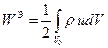 (27)
(27)
Если электростатическое поле создается поверхностными зарядами, распределенными по поверхности 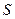 с плотностью
с плотностью 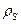 , то выражение для энергии электростатического поля принимает вид
, то выражение для энергии электростатического поля принимает вид
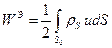 (28)
(28)
В случае распределения зарядов вдоль контура 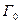 с плотностью
с плотностью 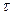 (заряженная нить):
(заряженная нить):
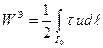 (29)
(29)
В общем случае при наличии зарядов всех трех типов
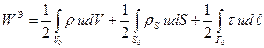
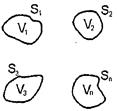
Рассмотрим частный случай, когда электростатическое поле создается зарядами, расположенными на проводниках. Пусть имеется 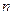 проводников (рис. 11), потенциалы которых равны соответственно
проводников (рис. 11), потенциалы которых равны соответственно 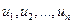 . Так как потенциал проводника имеет одинаковые значения во всех его точках, а заряды распределены по его поверхности, то, применяя формулу (28), получаем
. Так как потенциал проводника имеет одинаковые значения во всех его точках, а заряды распределены по его поверхности, то, применяя формулу (28), получаем
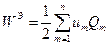 (30)
(30)
 где
где 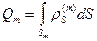
- полный заряд 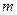 -го проводника, a
-го проводника, a 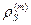 - плотность поверхностных зарядов, с которой заряд
- плотность поверхностных зарядов, с которой заряд 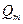 распределен по поверхности
распределен по поверхности 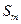
рассматриваемого проводника.
 Выражение для энергии уединенного проводника, т.е. бесконечно удаленного от других тел и зарядов, находится из формулы (30) как частный случай. Полагая в (30)
Выражение для энергии уединенного проводника, т.е. бесконечно удаленного от других тел и зарядов, находится из формулы (30) как частный случай. Полагая в (30) 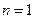 , получаем
, получаем
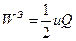 (31)
(31)
На энергию электростатического поля не распространяется принцип суперпозиции. Поэтому энергия системы проводников не равна суммарной энергии уединенных проводников. Представим потенциал 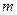 -го проводника в виде суммы:
-го проводника в виде суммы:
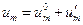 (32)
(32)
где 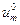 - потенциал уединенного проводника, а
- потенциал уединенного проводника, а 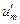 -потенциал, создаваемый действием всех остальных проводников. Подставляя (32) в (30), получаем
-потенциал, создаваемый действием всех остальных проводников. Подставляя (32) в (30), получаем
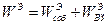 ,
,
где
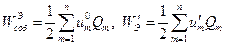
Величину 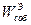 принято называть собственной энергией системы проводников, a
принято называть собственной энергией системы проводников, a 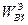 - взаимной энергией.
- взаимной энергией.
Можно показать, что заряды, находящиеся на системе заданных проводников, расположенных в диэлектрике, распределяются по поверхности этих проводников таким образом, что энергия получающегося в результате электростатического поля минимальна. Это важное утверждение известно под названием теоремы Томсона.
4. Емкость
Потенциал уединенного проводника зависит от его размеров и формы, а также от величины имеющегося на нем заряда. При равных потенциалах уединенные тела разной формы или размеров обладают зарядами разной величины. Отношение величины заряда к потенциалу при условии, что потенциалы бесконечно удаленных точек считаются равными нулю, называется емкостью уединенного проводника;
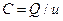 (33)
(33)
Емкость измеряют в фарадах (Ф = Кл/В). С учетом формулы (33) выражение для энергии электростатического поля уединенного заряженного проводника (31) принимает вид
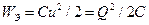 (34)
(34)
Если проводник не уединен, то потенциал, приобретаемый им при сообщении ему какого-либо заряда, существенно зависит от формы и расположения других проводников. Заряженные тела создают электрическое поле, под действием которого заряды на всех соседних проводящих телах перераспределяются. Перераспределение продолжается до тех пор, пока суммарное электрическое поле внутри каждого проводника не станет равным нулю.
Рассмотрим систему из 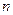 проводников с зарядами
проводников с зарядами 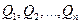 соответственно. Потенциал каждого проводника линейно зависит от величины зарядов
соответственно. Потенциал каждого проводника линейно зависит от величины зарядов 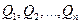 , т.е. должно выполняться п соотношений вида
, т.е. должно выполняться п соотношений вида
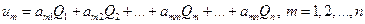 (35)
(35)
где 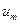 -потенциал т-го проводника, а
-потенциал т-го проводника, а 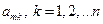 -некоторые постоянные, называемые потенциальными коэффициентами, зависящие от размеров, формы и взаимного расположения проводников. Коэффициент
-некоторые постоянные, называемые потенциальными коэффициентами, зависящие от размеров, формы и взаимного расположения проводников. Коэффициент 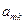 численно равен потенциалу
численно равен потенциалу 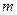 -го проводника, наведенному зарядом
-го проводника, наведенному зарядом 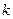 -го проводника при условии, что заряд последнего равен 1 Кл. а заряды остальных - нулю. Например,
-го проводника при условии, что заряд последнего равен 1 Кл. а заряды остальных - нулю. Например, 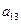 численно равен потенциалу проводника 1, наведенному единичным зарядом проводника при отсутствии зарядов на остальных проводниках.
численно равен потенциалу проводника 1, наведенному единичным зарядом проводника при отсутствии зарядов на остальных проводниках.
Система уравнений (35) определяет потенциалы проводников через заряды Q и потенциальные коэффициенты 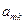 . Если потенциалы
. Если потенциалы 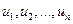 проводников и потенциальные коэффициенты
проводников и потенциальные коэффициенты 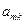 известны, то система (35) позволяет однозначно определить заряды проводников
известны, то система (35) позволяет однозначно определить заряды проводников
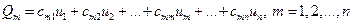 (36)
(36)
Постоянные коэффициенты 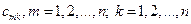 однозначно определяются потенциальными коэффициентами
однозначно определяются потенциальными коэффициентами 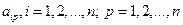 , и находятся при решении системы (35) относительно зарядов
, и находятся при решении системы (35) относительно зарядов 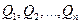 . Из уравнений (36) следует, что коэффициент
. Из уравнений (36) следует, что коэффициент 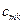 численно равен заряду
численно равен заряду 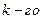 проводника, если потенциал с-го проводника равен единице, а потенциалы остальных проводников - нулю.
проводника, если потенциал с-го проводника равен единице, а потенциалы остальных проводников - нулю.
Отметим, что потенциальные коэффициенты 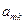 и коэффициенты
и коэффициенты 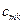 удовлетворяют правилу взаимности:
удовлетворяют правилу взаимности:
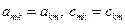 (37)
(37)
Обычно систему уравнений (36) записывают в несколько иной форме. Прибавим к правой части т-го уравнения системы равное нулю выражение 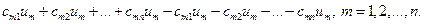 В результате получим следующую систему
В результате получим следующую систему 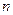 уравнений:
уравнений:
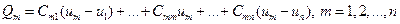
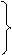 где
где
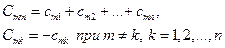 (38)
(38)
Коэффициенты 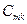 называют частичными емкостями. Иногда вводят различные названия для коэффициентов с одинаковыми и разными индексами: коэффициент
называют частичными емкостями. Иногда вводят различные названия для коэффициентов с одинаковыми и разными индексами: коэффициент 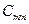 называют собственной емкостью
называют собственной емкостью 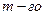 проводника, а
проводника, а 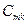 - взаимной емкостью
- взаимной емкостью 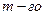 и
и 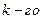 проводников. Отметим, что собственные емкости уединенных проводников могут отличаться от коэффициентов
проводников. Отметим, что собственные емкости уединенных проводников могут отличаться от коэффициентов 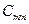 . Аналогично взаимные емкости двух проводников, отделенных от остальных, могут отличаться от соответствующих коэффициентов
. Аналогично взаимные емкости двух проводников, отделенных от остальных, могут отличаться от соответствующих коэффициентов 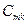 , так как частичные емкости
, так как частичные емкости 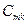 и
и 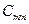 определяются не только рассматриваемыми проводниками, но и всеми остальными проводниками системы.
определяются не только рассматриваемыми проводниками, но и всеми остальными проводниками системы.
Из формул (3.36) и (3.37) следует, что частичные емкости также удовлетворяют правилу взаимности: 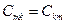 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|