
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Ранг матрицы.
Ранг матрицы.
Пусть дана прямоугольная матрица A(m 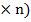 , имеющая m строк и n столбцов. Обозначим столбцы матрицы
, имеющая m строк и n столбцов. Обозначим столбцы матрицы 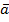 1,
1, 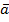 2,…,
2,…, 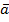 n, где
n, где 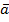 1 =
1 = 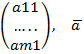 2 =
2 = 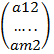 ,…,
,…, 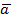 n =
n = 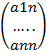
Система из n столбцов одной и той же размерности называется линейно зависимой, если существуют такие числа β1, β2, … , βn, не все одновременно равные нулю, что β1∙ 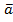 1 + β2 ∙
1 + β2 ∙ 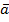 2 + … + βn ∙
2 + … + βn ∙ 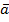 n =
n = 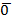 , где
, где 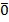 - нулевой столбец той же размерности.
- нулевой столбец той же размерности.
Система из n столбцов одной и той же размерности называется линейно зависимой, если равенство β1 ∙ 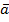 1 + β2 ∙
1 + β2 ∙ 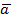 2 + … + βn ∙
2 + … + βn ∙ 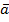 n =
n = 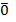 возможно только при β1 = β2 =…. = βn=0.
возможно только при β1 = β2 =…. = βn=0.
Перечислим свойства, связанные с понятиями линейной зависимости и линейной независимости.
1.Система из n столбцов (n>1) линейно зависима, если один из столбцов есть линейная комбинация остальных.
Замечание: это свойство можно рассматривать как второе определение линейной зависимости.
2.Если в систему столбцов входит нулевой столбец, или два пропорциональных столбца, то система линейно зависима.
3.Если часть столбцов составляет линейно зависимую подсистему, то и вся система из n столбцов – линейно зависима.
4.Если система столбцов линейно независима, то и любая ее подсистема тоже линейно независима.
Аналогично формулируются утверждения о линейной комбинации строк одной и той же размерностью. Определение важного в линейной алгебре понятия ранг матрицы – наиболее характерная задача при проверке на совместность системы алгебраических уравнений.
Рангом матрицы(rang A, rg A) называется максимальное число линейно независимых строк (столбцов) матрицы A. Рангом матрицы A, размерностью (m  n), является порядок r базисного минора, если минор отличен от нуля, а все миноры порядка (r + 1) равны нулю или вовсе не существуют. Ранг матрицы A равен нулю, если все элементы матрицы aij = 0. Любой элемент aij ≠ 0 матрицы A(m
n), является порядок r базисного минора, если минор отличен от нуля, а все миноры порядка (r + 1) равны нулю или вовсе не существуют. Ранг матрицы A равен нулю, если все элементы матрицы aij = 0. Любой элемент aij ≠ 0 матрицы A(m  n) является минором 1-ого порядка.
n) является минором 1-ого порядка.
Строки (столбцы) матрицы, содержащие базисный минор, линейно независимы, а остальные строки (столбцы) матрицы являются их линейной комбинацией. Базисных миноров может быть несколько, но все они имеют одинаковый порядок. Ранг матрицы можно находить методом окаймляющих миноров или методом элементарных преобразований матрицы.
Метод окаймляющих миноров. Вычисление ранга матрицы с помощью этого метода надо вести от миноров низшего порядка к минорам более высокого порядка. Если хотя бы один элемент матрицы не равен нулю, то он уже является минором 1-ого порядка. Вычисляем окаймляющие его миноры 2-ого порядка, пока не получим среди них отличный от нуля. Затем рассматриваем миноры 3-ьего порядка, окаймляющие минор 2-ого порядка и т.д. Метод подходит для определения ранга матрицы небольшой размерности.
Примеры. A =  , минор
, минор 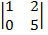 ≠ 0 – может являться базисным минором, а все миноры 3-ьего порядка равны нулю, следовательно, rang A = 2.
≠ 0 – может являться базисным минором, а все миноры 3-ьего порядка равны нулю, следовательно, rang A = 2.
A = 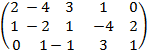 начнем вычисление ранга матрицы с элемента a11 = 2 ≠ 0, т.е. с минора 1-ого порядка. Рассмотрим минор 2-ого порядка, окаймляющий элемент a11 = 2.
начнем вычисление ранга матрицы с элемента a11 = 2 ≠ 0, т.е. с минора 1-ого порядка. Рассмотрим минор 2-ого порядка, окаймляющий элемент a11 = 2. 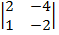 = - 4 + 4 = 0, рассмотрим другой минор 2-ого порядка
= - 4 + 4 = 0, рассмотрим другой минор 2-ого порядка 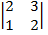 = 2 – 3 = -1 ≠ 0, т.е. rang A = 2. Рассмотрим теперь минор 3-ьего порядка
= 2 – 3 = -1 ≠ 0, т.е. rang A = 2. Рассмотрим теперь минор 3-ьего порядка 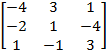 = = (-4∙1∙3 + 1∙(-2)∙(-1)+3∙(-4)∙1) – (1∙1∙1+3∙(-2)∙3 - 4∙(-4)∙(-1)) = -22 + 33 = 11 ≠ 0. Итак, rang A=3.
= = (-4∙1∙3 + 1∙(-2)∙(-1)+3∙(-4)∙1) – (1∙1∙1+3∙(-2)∙3 - 4∙(-4)∙(-1)) = -22 + 33 = 11 ≠ 0. Итак, rang A=3.
Замечание. Если в матрице A все миноры порядка rравны нулю, то равны нулю и все миноры более высокого порядка (если таковые существуют).
Нахождение ранга матрицы методом элементарных преобразований. Элементарными преобразованиями матрицы являются следующие.
1.Перестановка строк (столбцов) матрицы.
2.Умножение всех элементов некоторого столбца (строки) на число, отличное от нуля.
3.Прибавление ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Теорема. При элементарных преобразованиях ранг матрицы не меняется.
Задачи на вычисление ранга матрицы с помощью метода элементарных преобразований.
Задача 1. Определить ранг матрицы:
A = 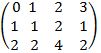 - размерность матрицы (3
- размерность матрицы (3  4), наибольший возможный ранг матрицы равен 3. Начнем элементарные преобразования матрицы: из элементов 3-ьей строки вычтем элементы 2-ой строки (
4), наибольший возможный ранг матрицы равен 3. Начнем элементарные преобразования матрицы: из элементов 3-ьей строки вычтем элементы 2-ой строки (  - знак эквивалентных преобразований)
- знак эквивалентных преобразований) 
 - получили 3-ью строку нулевую, следовательно, если какой-либо минор 2-ого порядка окажется не равным нулю, то ранг будет равен двум. Действительно минор
- получили 3-ью строку нулевую, следовательно, если какой-либо минор 2-ого порядка окажется не равным нулю, то ранг будет равен двум. Действительно минор 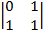 = -1 ≠ 0, т.е. rang A = 2.
= -1 ≠ 0, т.е. rang A = 2.
Задача 2. Вычислить ранг матрицы.
A = 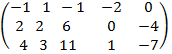 , т.к. матрица содержит часть элементов, отличных от нуля, то rang A
, т.к. матрица содержит часть элементов, отличных от нуля, то rang A 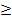 1, но размерность матрицы (3
1, но размерность матрицы (3 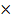 5), следовательно rang A≤3.
5), следовательно rang A≤3. 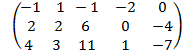
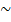
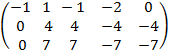 - умножили 1-ю строку на два и сложили со второй, а затем 1-ю строку умножили на четыре и сложили с 3-ьей строкой. Строки 2-я и 3-ья оказались линейно зависимыми, следовательно, в матрице A две линейно независимые строки. Rang A = 2.
- умножили 1-ю строку на два и сложили со второй, а затем 1-ю строку умножили на четыре и сложили с 3-ьей строкой. Строки 2-я и 3-ья оказались линейно зависимыми, следовательно, в матрице A две линейно независимые строки. Rang A = 2.
Задача 3. Найти ранг матрицы и определить количество линейно независимых строк (столбцов).
A = 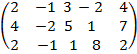 , матрица содержит элементы отличные от нуля, но размерность матрицы (3
, матрица содержит элементы отличные от нуля, но размерность матрицы (3 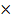 5), следовательно 1
5), следовательно 1 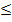 rang A
rang A 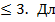 я вычисления ранга матрицы воспользуемся элементарными преобразованиями. Вычтем из элементов 2-ой строки элементы 1-ой строки, умноженные на два, а из элементов 3-ьей строки вычтем элементы 1-ой строки.
я вычисления ранга матрицы воспользуемся элементарными преобразованиями. Вычтем из элементов 2-ой строки элементы 1-ой строки, умноженные на два, а из элементов 3-ьей строки вычтем элементы 1-ой строки.
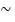
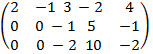
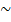
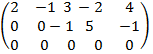 - вторая и третья строки содержали пропорциональные элементы, следовательно, матрица содержит две линейно независимые строки. Ранг матрицы равен количеству линейно независимых строк (столбцов), т.е. rang A= 2.
- вторая и третья строки содержали пропорциональные элементы, следовательно, матрица содержит две линейно независимые строки. Ранг матрицы равен количеству линейно независимых строк (столбцов), т.е. rang A= 2.
Задача 4. Проверить является ли система арифметических векторов а1 = (2, -3, 1), а2 = (3, -1, 5), а3 = (1, -5, -3) линейно зависимой или линейно независимой.
Запишем матрицу А, вектор-столбцами которой являются вектора а1, а2, а3. A = 
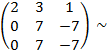
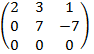 - воспользовались методом элементарных преобразований: к 2-ой строке, умноженной на два прибавили 1-ю строку, умноженную на три; из 3-ьей строки, умноженной на два вычли 1-ю строку. В результате две последние строки оказались с одинаковыми элементами. Rang A = 2, система векторов оказалась линейно зависима. Минор M2 =
- воспользовались методом элементарных преобразований: к 2-ой строке, умноженной на два прибавили 1-ю строку, умноженную на три; из 3-ьей строки, умноженной на два вычли 1-ю строку. В результате две последние строки оказались с одинаковыми элементами. Rang A = 2, система векторов оказалась линейно зависима. Минор M2 = 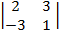 = 2∙(-1) – (-3)∙3 = -2 + 9 = 7 ≠ 0, следовательно, этот минор может быть принят как базисный. Вектора а1 и а2 образуют базис исходной системы.
= 2∙(-1) – (-3)∙3 = -2 + 9 = 7 ≠ 0, следовательно, этот минор может быть принят как базисный. Вектора а1 и а2 образуют базис исходной системы.
Замечание. Базой данной системы векторов называется такая ее подсистема, которая обладает следующими свойствами: а) эта подсистема линейно независима; б) любой вектор всей системы линейно выражается через векторы этой системы.
Теорема о базисном миноре. Ранг матрицы равен рангу ее столбцов (строк), при этом система столбцов (строк) матрицы, содержащая базисный минор, образует базис в системе всех столбцов (строк) этой матрицы.
Задача 5. Найти все значения β, при которых вектор b = (7, -2, β) линейно выражается через векторы а1 = (2, 3, 5), а2 = (3, 7, 8), а3 (1, -6, 1). Составим матрицу A, вектор-столбцами которой являются четыре вышеуказанных вектора. Методом элементарных преобразований будем искать ранг матрицы.
A = 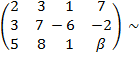
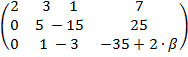
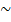
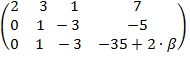 – из 2-ой и 3-ьей строк, умноженных на два вычитали 1-ю строку, умноженную соответственно на три и на пять. -35 + 2 ∙ β = -5, 2∙ β = 30, при β = 15 система векторов линейно зависима и вектор b можно выразить через векторы а1, а2, а3.
– из 2-ой и 3-ьей строк, умноженных на два вычитали 1-ю строку, умноженную соответственно на три и на пять. -35 + 2 ∙ β = -5, 2∙ β = 30, при β = 15 система векторов линейно зависима и вектор b можно выразить через векторы а1, а2, а3.
Задача 6. Найти все значения 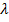 , при которых вектор x = (1, 3,
, при которых вектор x = (1, 3, 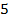 ) линейно выражается через векторы а1 = (3, 2, 5), а2 = (2, 4, 7), а3 = (5, 6,
) линейно выражается через векторы а1 = (3, 2, 5), а2 = (2, 4, 7), а3 = (5, 6, 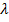 ). Составим матрицу A =
). Составим матрицу A = 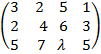
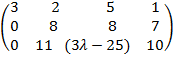 , если (3
, если (3 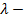 25) ≠ 11, т.е.
25) ≠ 11, т.е. 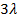 ≠ 36, и
≠ 36, и 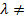 12, то вектор x - может являться линейной комбинацией векторов а1, а2, а3.
12, то вектор x - может являться линейной комбинацией векторов а1, а2, а3.
Задача 7. Найти все базы системы векторов: а1 = (1, 2, 3), а2 = (2, 3, 4), а3 = (3, 2, 3), а4 = (4, 3, 4), а5 = (1, 1, 1). Составим матрицу системы векторов A = 
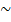 ранг матрицы будем искать методом элементарных преобразований: из 2-ой и 3-ьей строк вычтем 1-ю строку соответственно умноженную на два и на три;
ранг матрицы будем искать методом элементарных преобразований: из 2-ой и 3-ьей строк вычтем 1-ю строку соответственно умноженную на два и на три; 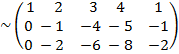
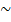
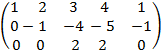 , в следующем преобразовании из элементов 3-ьей строки вычитали элементы 2-ой (новой) строки, умноженной на два. В результате получили, что базами могут быть векторы: а1, а2, а3, т.к. определитель 3-ьего порядка, составленный из этих векторов не равен нулю; а также система векторов а2 , а3, а4, т.к.
, в следующем преобразовании из элементов 3-ьей строки вычитали элементы 2-ой (новой) строки, умноженной на два. В результате получили, что базами могут быть векторы: а1, а2, а3, т.к. определитель 3-ьего порядка, составленный из этих векторов не равен нулю; а также система векторов а2 , а3, а4, т.к. 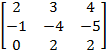 = (2∙(-4)∙2 + (-1)∙2∙4 + 0∙3∙4)-(0∙(-4)∙4 + 3∙(-1)∙2 + 2∙2∙(-5))=8+26=34≠0 Системы векторов а1, а2, а5 и векторов а3, а4, а5, не могут образовывать базу, т.к. определители 3-ьего порядка составленные из этих векторов равны нулю. Следовательно, любые три других вектора образуют базу.
= (2∙(-4)∙2 + (-1)∙2∙4 + 0∙3∙4)-(0∙(-4)∙4 + 3∙(-1)∙2 + 2∙2∙(-5))=8+26=34≠0 Системы векторов а1, а2, а5 и векторов а3, а4, а5, не могут образовывать базу, т.к. определители 3-ьего порядка составленные из этих векторов равны нулю. Следовательно, любые три других вектора образуют базу.
Упражнения для самостоятельной работы.
1.Найти все значения 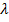 , при которых вектор b = (
, при которых вектор b = ( 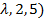 линейно выражается через векторы а1 = (3, 2, 6), а2 = (7, 3, 9), а3 = (5, 1, 3). (Ответ: ни при каких
линейно выражается через векторы а1 = (3, 2, 6), а2 = (7, 3, 9), а3 = (5, 1, 3). (Ответ: ни при каких  ).
).
2.Найти ранг и все базы системы векторов: а1 = (1, 2, 0, 0), а2 = (1, 2, 3, 4), а3 = (3, 6, 0, 0). Ответ: rang = 2, базы – а1 и а2, а2 и а3.
3.Найти все базы системы векторов: а1 = (2, 1, -3, 1), а2 = (4, 2, -6, 2), а3 = (6, 3, -9,3), а4 = (1, 1, 1, 1). Ответ: а1 , а4 ; а2 , а4 ; а3 , а4.
4.Найти какую-нибудь базу системы векторов: а1 = (5, 2, -3, 1), а2 = (4, 1, -2, 3), а3 = (1, 1, -1, -2), а4 = (3, 4, -1, 2), и все векторы системы, не входящие в данную базу, выразить через векторы базы. Ответ: базу могут образовать, например, векторы а1, а2, а4, в этом случае вектор а3 = а1 – а2.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|