
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример решения домашнего задания по теме «Векторная алгебра»
Пример решения домашнего задания по теме «Векторная алгебра»
5. Для данных в пространстве точек 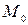 ,
, 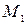 ,
,  ,
, 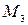 :
:
а) найти координаты и модули векторов 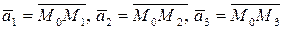 ;
;
б) найти единичный вектор, являющийся ортом вектора 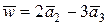 ;
;
в) найти угол между векторами 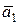 и
и 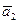 ;
;
г) найти площадь треугольника, построенного на векторах 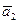 и
и 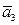 ;
;
д) найти объём пирамиды, построенной на векторах 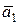 ,
, 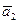 и
и 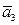 ;
;
е) определить, являются ли векторы 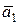 ,
, 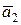 и
и 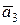 компланарными, а также попарно коллинеарными, перпендикулярными.
компланарными, а также попарно коллинеарными, перпендикулярными.
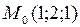 ,
, 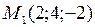 ,
, 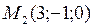 ,
, 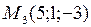 .
.
а) найти координаты и модули векторов 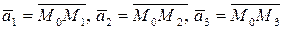 ;
;
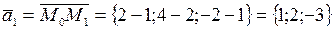 ;
;
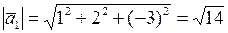 .
.
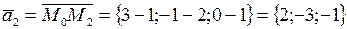 ;
;
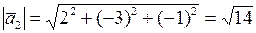 .
.
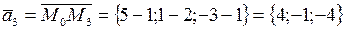 ;
;
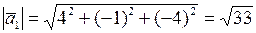 .
.
б) найти единичный вектор, являющийся ортом вектора 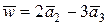 ;
;
Найдём координаты вектора 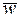 :
:
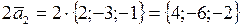 ;
;
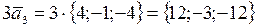 ;
;
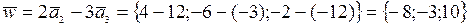 ;
;
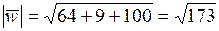 .
.
Орт вектора 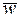 :
:
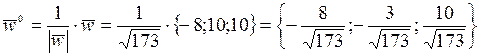 .
.
в) найти угол между векторами 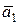 и
и 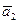 ;
;
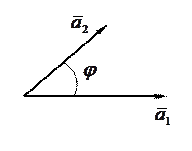 Пусть
Пусть 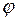 - угол между векторами
- угол между векторами 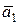 и
и 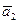 ; тогда
; тогда 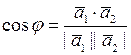 .
.
Так как 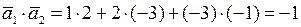 ,
,
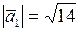 ,
, 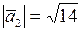 , то
, то
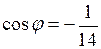 ,
, 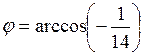 .
.
г) найти площадь треугольника, построенного на векторах 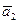 и
и 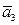 ;
;
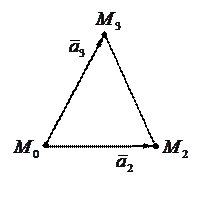
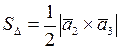 .
.

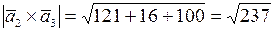 ;
;
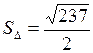 .
.
д) найти объём пирамиды, построенной на векторах 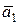 ,
, 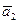 и
и 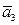 ;
;
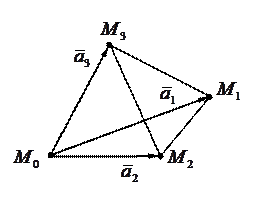
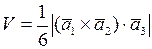 ,
,
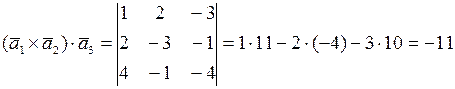 ;
;
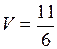 .
.
е) определить, являются ли векторы 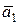 ,
, 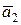 и
и 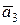 компланарными, а также попарно коллинеарными, перпендикулярными.
компланарными, а также попарно коллинеарными, перпендикулярными.
Так как 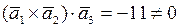 , то векторы
, то векторы  ,
, 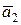 и
и 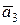 не компланарны.
не компланарны.
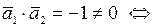
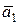 и
и 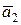 не перпендикулярны;
не перпендикулярны;
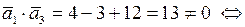
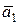 и
и 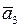 не перпендикулярны;
не перпендикулярны;
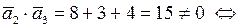
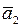 и
и 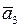 не перпендикулярны.
не перпендикулярны.
Векторы 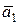 и
и 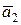 не коллинеарны так как
не коллинеарны так как 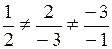 ;
;
векторы 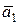 и
и 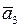 не коллинеарны так как
не коллинеарны так как 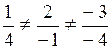 ;
;
Векторы 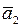 и
и 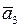 не коллинеарны так как
не коллинеарны так как 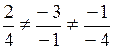 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|