Тема: Площадь поверхности призмы

Тема: Площадь поверхности призмы

Задание:

1.Записать примеры 1-2;

2.Решить 3 задачи.

3.Решенные задачи сфотографировать и отправить на почту nastyusha_sergeevna_91@list.ru

Пример №1.

Основанием прямой призмы является равнобедренная трапеция с основаниями 21см и 9 см и высотой 8 см (рис. 1). Найдите площадь боковой поверхности, если боковое ребро равно 10 см.

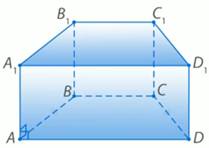
Рис. 1

Дано:

АД ∥ ВС, АВ = СД,

AД = 21см, ВС = 9см, ВН = 8 см,

АА_! ⊥ АВС, АА₁ = 10 см. (рис. 4)

Найти: s_бок

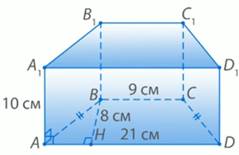
Рис. 2

Решение:

Рассмотрим трапецию АВСД (рис. 3). ВН и СД – высоты трапеции. AД = 21см, bВС = 9см. Так как трапеция АВСДравнобокая, то НД =В С = 9

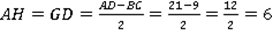см

(см).

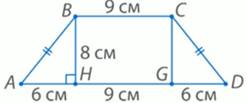
Рис. 3

Рассмотрим треугольник ∆авн и найдем сторону ав по теореме пифагора:

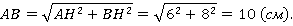
Найдем периметр основания.

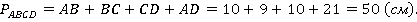
Применяем формулу для площади боковой поверхности:

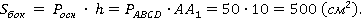
Ответ: 500 см²

Пример №2.

Докажите, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Комментарий к решению: доказательство проведём на пример №е треугольной призмы.

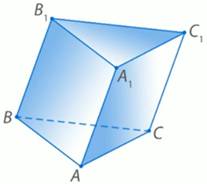
Рис. 4

Рассмотрим треугольную призму АВСА₁В₁С₁. Построим плоскость перпендикулярного сечения. На ребре ВВ₁ выберем точку К (рис. 4). Через точку К можно проведём перпендикуляр КL в плоскости этой грани АА₁В₁В к ребру ВВ₁. Этот перпендикуляр будет перпендикуляром и к АА₁, так как прямые АА₁ и ВВ₁ параллельны..

Теперь проведём перпендикуляр КМ перпендикулярно ребру ВВ₁ в плоскости грани ВВ₁С_1С.

Получаем, что боковое ребро ВВ₁ перпендикулярно двум пересекающимся прямым КL и КМ плоскости КLМ . Значит, ВВ₁ - перпендикуляр к плоскости КLМ .

То есть, построенное сечение КLМ перпендикулярно боковому ребру. Надо доказать, что площадь боковой поверхности равняется произведению периметра перпендикулярного сечения КLМ на боковое ребро ВВ₁. То есть, имеем следующую задачу.

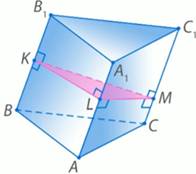
Рис. 5

Дано: АВСА₁В₁С₁ – наклонная призма,

ВВ₁ ⊥ . КLМ

Доказать: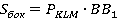

Доказательство:

Любая боковая грань призмы – это параллелограмм. Рассмотрим грань АВВ₁А₁. KL – это высота параллелограмма АВВ₁А₁.. Поэтому площадь параллелограмма АВВ₁А₁. записывается следующим образом:

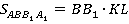
Аналогично, , .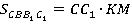

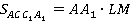В призме все боковые ребра равны, АА₁ = ₁ = сс₁. Запишем, чему равна площадь боковой поверхности.

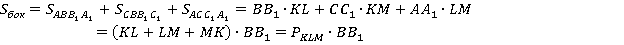
Мы показали, что 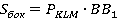. Задача доказана.

Задания:

1.Основание прямой призмы – прямоугольный треугольник, диагонали боковых граней призмы 8 см, 14 см, 16 см. Найдите высоту призмы.

2.Основание прямой призмы – прямоугольный треугольник с катетами 15 и 20 см. Большая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.

3.Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота – 8.