
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Матрицы и определители. Теоретический материал
Матрицы и определители
Теоретический материал
Матрицейназывается прямоугольная таблица чисел, состоящая из m строк и n столбцов:
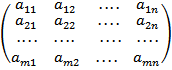
aij - элементы матриц. Индекс i -номер строки; Индекс j-номер столбца.
Числа mи nуказывают размерность матрицы.
Например: 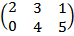 в матрице две строки и три столбца.
в матрице две строки и три столбца.
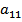 =2;
=2; 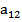 =3;
=3; 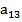 =1;
=1; 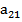 =0;
=0;  =4;
=4; 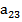 =5.
=5.
Если m = n, то матрица называется квадратной.
Например: 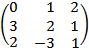 Квадратная матрица размерности 3.
Квадратная матрица размерности 3.
Сложение матриц:
Сложение матриц (вычитание матриц) одинакового размера осуществляется поэлементно:
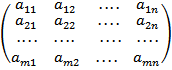 +
+ 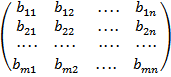 =
= 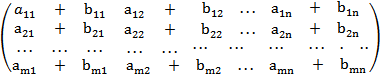
Умножение матрицы на число:
Каждый элемент матрицы умножается на число.
A= 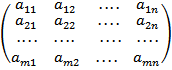 λ-число
λ-число
λA= 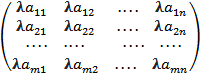
Умножение матриц:
Умножение матрицы A на матрицу B определено, если число столбцов первой матрицы
равно числу строк второй. Тогда произведением матрицы 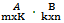 называется матрица C
называется матрица C
размерностью m x n, где каждый элемент Cij равен сумме произведений элементов i строки, матрицы A на соответствующие элементы j столбца матрицы B.
Пример:
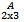 =
= 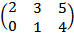
 =
= 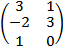
A·B= 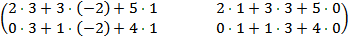 =
= 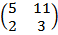
Транспонирование матрицы:
Матрица  называется транспонированной к матрице A, если столбцы матрицы A являются строками матрица
называется транспонированной к матрице A, если столбцы матрицы A являются строками матрица  .
.
A= 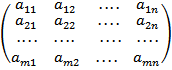

Матрица E= 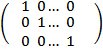 называется единичной матрицей.
называется единичной матрицей.
Матрица 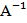 называется матрицей, обратной квадратной матрице А, если
называется матрицей, обратной квадратной матрице А, если 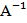 ·А=А·
·А=А· 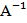 =Е
=Е
Для квадратных матриц вводится понятие определителя
A= 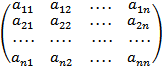 |A|=
|A|= 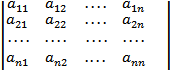 - определитель
- определитель
Определитель |A| находится по следующему правилу:
- Если А содержит только один элемент 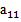 , то|
, то| 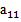 |=
|= 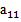 , т.е. определитель совпадает с данным элементом;
, т.е. определитель совпадает с данным элементом;
- Если размерность матрицы А равна n, то ее определитель можно вычислить в виде линейной комбинации n определителей (n-1) порядка
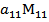 -
- 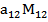 +
+ 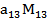 -...+
-...+ 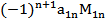 ,где
,где
M1j - определитель матрицы, которая получается, если из матрицы А вычеркнуть первую строку и j-ый столбец.
Например:
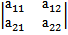 =
= 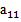 ·|
·|  -
-  ·|
·| 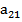 |=
|=  -
- 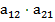
Для определителя третьего порядка :
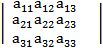 =
= 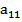
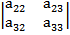 -
- 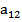
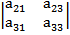 +
+ 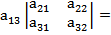
= 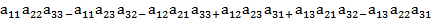
Эти выражения можно получить по следующим схемам:
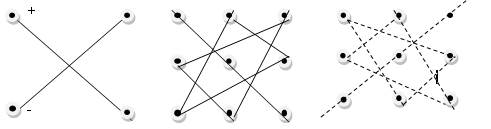
а11а22а33 + а31а12а23 + а13а21а32 – а13а22а31 – а11а23а32 – а33а12а21
Практическое задание
1). Для данных матриц А и В выполнить действия: А∙В; В∙А; АТ∙В
| Вариант | |||||
А
В
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)