
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вычислите самостоятельно, а на стр. 2и 3, я размещу решения для самопроверки.
Ребята, здравствуйте!
Сегодня мы с вами будем повторять производную. Вычисление производных.
Я надеюсь, вы посмотрели небольшой видеоурок, посвященный данной теме.
Рассмотрим несколько заданий, которые будут предложены в контрольной работе.
1. Пользуясь правилами и формулами нахождения производных, найдите производную функции:
а) у = 2х7; б) у = 8; в) у = 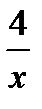 ; г) у = 13 + 6х; д) у = 5
; г) у = 13 + 6х; д) у = 5 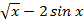 ;
;
е) у = 2 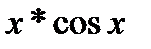 ; ж) у =
; ж) у = 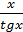 ;
;
Вычислите самостоятельно, а на стр. 2и 3, я размещу решения для самопроверки.
2. Решите уравнение: f / (x) = 0,если f(x) = x3 – x4
3. Решите неравенство: f / (x)< 0, если f(x) = 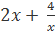
Попробуйте тоже самостоятельно разобрать его, а решение на стр.2
1. Пользуясь правилами и формулами нахождения производных, найдите производную функции:
а) у = 2х7; б) у = 8; в) у = 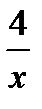 ; г) у = 13 + 6х; д) у = 5
; г) у = 13 + 6х; д) у = 5 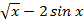 ;
;
е) у = 2 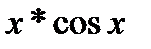 ; ж) у =
; ж) у = 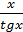 ;
;
Решение:
а) у/ = 7*2 x6 = 14 x6
б) y/ = 0
в) y/ = 4 * 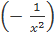 = -
= - 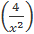
г) y/ = 0 + 6 = 6
д) y/ = 5 * 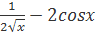
е) y/ = (2x)/ * cos x + (cos x)/ * 2x = 2cos x – 2x * sin x
ж) y/ =  =
= 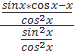 =
= 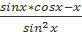
2. Решите уравнение: f / (x) = 0,если f(x) = x3 – x4
Решение: Найдем производную данной функции: f / (x) = 3 х2 – 4 х3
Составим уравнение: 3 х2 – 4 х3 = 0
х2 (3 – 4 х) = 0. Произведение двух множителей равно нулю тогда и только тогда, когда ….
х2 = 0 или 3 – 4х = 0
х = 0 или 4х = 3. Следовательно х = 
Ответ: 0; 
3. Решите неравенство: f / (x)< 0, если f(x) = 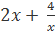
Решение: Найдем производную данной функции:
f / (x) = 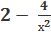
Составим неравенство: 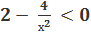
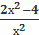

Решаем дробно – рациональное неравенство. Приравниваем к нулю и числитель дроби, и знаменатель:
2х2 – 4 = 0
х2 – 2 = 0
х2 = 2
х = 
Знаменатель дроби должен быть отличен от нуля.
х 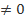
+ ___ ___ +
-  0
0 
Ответ: (- 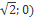 U (0;
U (0; 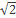 )
)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|