Практическое занятие №64. Декартовы координаты в пространстве

Сведения из теории:

Длиной отрезка АВ называется расстояние между точками А и В при заданном масштабе (отрезке единичной длины). Длину отрезка АВ будем обозначать как .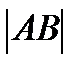

Расстояние между двумя точкамиA₁(x₁; y₁) и A₂(x₂; y₂) в прямоугольной системе координат выражается формулой:

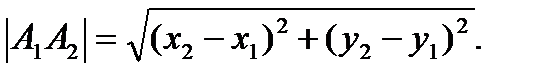
Точка С называется серединой отрезка АВ, если она лежит на отрезке АВ и находится на одинаковом расстоянии от его концов, т. е.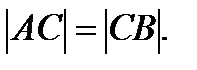

Координаты середины отрезка на плоскости

Введем прямоугольную декартову систему координат Оxy на плоскости. Пусть нам даны две точки А(х_А; у_А) и В(х_В; у_В) и известно, что точка С – середина отрезка АВ. Найдем координаты х_С и у_С точки С.

Рассмотрим случай, когда точки А и В не совпадают и не лежат одновременно на одной из координатных осей или на прямой, перпендикулярной одной из координатных осей.

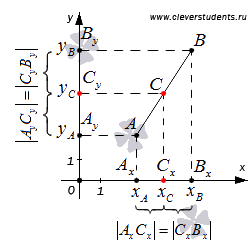
. Координаты середины отрезка

По построению:

.

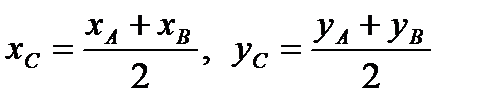Т. о., середина отрезка АВ на плоскости с концами в точках А(х_А; у_А) и В(х_В; у_В) имеет координаты .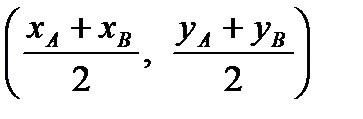

Пример

На плоскости заданы координаты двух точек А(-7; 3), В(2; 4). Найдите координаты середины отрезка АВ.

Решение:

пусть точка С – середина отрезка АВ. Ее координаты равны полусуммам соответствующих координат точек А и В:

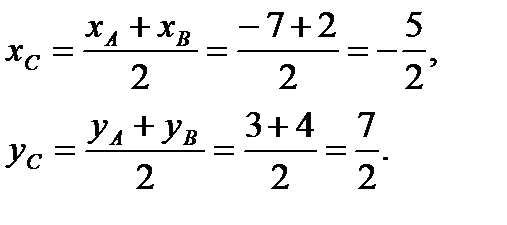
Т. о., середина отрезка АВ имеет координаты .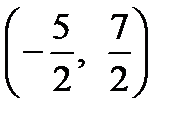

Часто с нахождением координат середины отрезка связаны задачи, в которых фигурирует термин «медиана».

Пример

Найдите длину медианы АМ в треугольнике АВС, если известны координаты его вершин А(-1; 0), В(3; 2), С(9; -8).

Решение:

т. к. АМ – медиана, то точка М является серединой стороны ВС. Найдем координаты середины этого отрезка по известным координатам его концов:

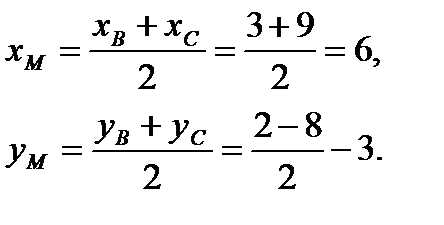
Т. о., М(6; -3).

Осталось воспользоваться формулой для вычисления расстояния между точками А и М:

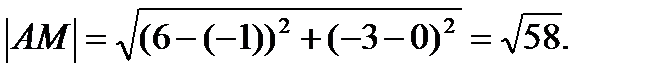
Существуют различные задачи, в которых известны координаты середины отрезка и одного из его концов, а требуется найти координаты другого конца. Рассмотрим решение одной из них.

Пример

В прямоугольной системе координат трехмерного пространства дан параллелепипед ABCDA₁B₁C₁D₁. Известно, что C₁(1; 1; 0), а М(4; 2; -4) – середина диагонали BD₁. Найдите координаты точки А.

Решение:

диагонали параллелограмма пересекаются в одной точке, и эта точка является серединой каждой из этих диагоналей. Таким образом, мы можем утверждать, что точка М является серединой отрезка AC₁ . Из формул для нахождения координат середины отрезка имеем:

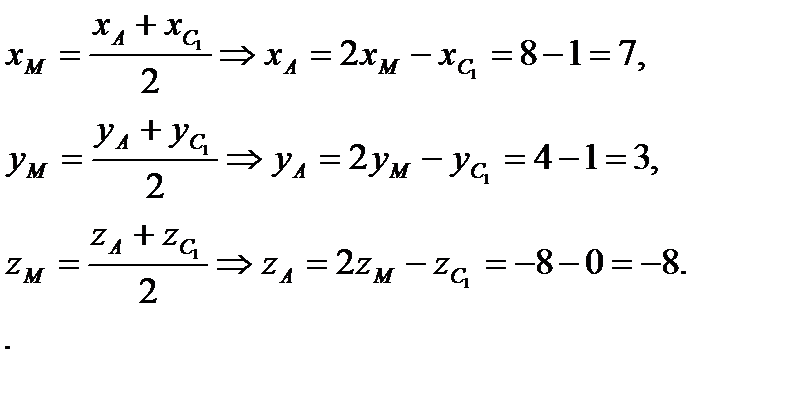
Итак, точка А имеет координаты (7; 3; -8).

Задания для самостоятельного решения:

1) Вычислите периметр треугольника АВС, если А(4; 0), В(12; -2), С(5; -9).

2) Вычислите длину медианы АМ треугольника АВС, вершины которого имеют координаты А(0; 1), В(1; -4), С(5; 2).

3) Докажите, что треугольник АВС – равнобедренный и вычислите его площадь, если вершины которого имеют координаты А(-4; 1), В(-2; 4), С(0; 1).

4) Докажите, что четырехугольник АBCD является параллелограммом, и вычислите его диагонали, если А(1; 1), B(6; 1), C(7; 4), D(2; 4).

5) Докажите, что четырехугольник АBCD является прямоугольником, и вычислите его площадь, если А(-3; -1), B(1; -1), C(1; -3), D(-3; -3).

Контрольные вопросы:

1. Запишите формулу для вычисления координат середины отрезка.

2. Запишите формулу для вычисления расстояния между двумя точками