
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие №65. Векторы
Практическое занятие №65
Векторы
Цель работы:
обучающийся должен:
знать:
- правила сложения векторов;
уметь:
- строить сумму векторов по правилу треугольника, параллелограмма;
- вычислять координаты суммы векторов.
Сведения из теории:
Линейные операции над векторами
Суммой двух векторов 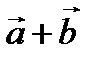 называется вектор, который идет из начала вектора
называется вектор, который идет из начала вектора 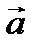 в конец вектора
в конец вектора 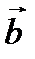 при условии, что вектор
при условии, что вектор 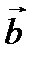 приложен к концу вектора
приложен к концу вектора 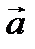 (правило треугольника).
(правило треугольника).
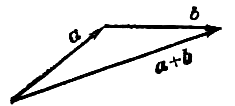
. Правило треугольника
Наряду с правилом треугольника часто пользуются (равносильным ему) правилом параллелограмма: если векторы 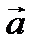 и
и 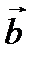 приведены к общему началу и на них построен параллелограмм, то сумма
приведены к общему началу и на них построен параллелограмм, то сумма 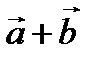 есть вектор, совпадающий с диагональю этого параллелограмма, идущей из общего начала
есть вектор, совпадающий с диагональю этого параллелограмма, идущей из общего начала 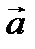 и
и 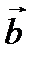 . Отсюда сразу следует, что
. Отсюда сразу следует, что 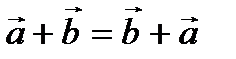 .
.
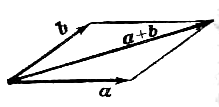
. Правило параллелограмма
Сложение многих векторов производится при помощи последовательного применения правила треугольника, построим сумму четырех векторов 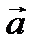 ,
, 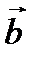 ,
, 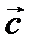 ,
, 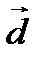 .
.
. Правило многоугольника
Разность двух векторов 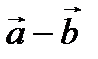 называется вектор, который в сумме с вектором
называется вектор, который в сумме с вектором 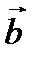 составляет вектор
составляет вектор 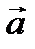 . Если два вектора
. Если два вектора 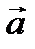 и
и 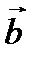 приведены к общему началу, то разность их есть вектор, идущий из конца
приведены к общему началу, то разность их есть вектор, идущий из конца 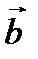 («вычитаемого») к концу
(«вычитаемого») к концу 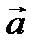 («уменьшаемого»).
(«уменьшаемого»).
Два вектора равной длины, лежащие на одной прямой и направленные в противоположные стороны, называются взаимно обратными: если один из них обозначен символом 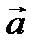 , то другой обозначается символом -
, то другой обозначается символом - 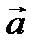 . Легко видеть, что
. Легко видеть, что 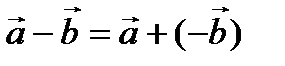 . Т. о., построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».
. Т. о., построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».
 Три вектора в пространстве можно складывать по правилу параллелепипеда: если на трех векторах
Три вектора в пространстве можно складывать по правилу параллелепипеда: если на трех векторах 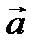 ,
, 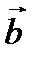 ,
, 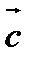 , как на ребрах, построить параллелепипед, то его диагональ, выходящая из общего начала данных векторов, и будет их суммой
, как на ребрах, построить параллелепипед, то его диагональ, выходящая из общего начала данных векторов, и будет их суммой 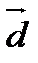 =
= 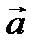 +
+ 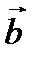 +
+ 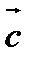 :
:
Рисунок 84. Правило параллелепипеда
Задания для самостоятельного решения:
1) По данным векторам 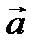 и
и 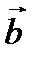 построить каждый из следующих векторов: 1)
построить каждый из следующих векторов: 1) 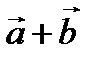 , 2)
, 2) 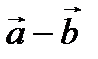 , 3)
, 3) 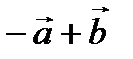 , 4)
, 4) 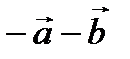 .
.
При сложении векторов складываются их соответствующие координаты, при вычитании вычитаются соответствующие координаты, т.е. если даны координаты векторов 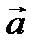 и
и 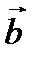 ,
, 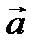 =(х1, у1, z1),
=(х1, у1, z1), 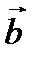 =(х2, у2, z2) и
=(х2, у2, z2) и 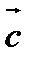 =
= 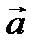 +
+ 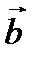 ;
; 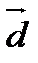 =
= 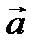 -
- 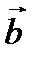 , то координаты векторов
, то координаты векторов 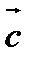 и
и 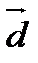 вычисляются по формулам:
вычисляются по формулам:
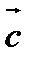 =(х1+х2; у1+у2; z1+z2),
=(х1+х2; у1+у2; z1+z2),
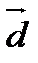 =(x1-x2; y1-y2; z1-z2).
=(x1-x2; y1-y2; z1-z2).
Пример
Вычислить координаты векторов 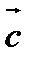 =
= 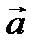 +
+ 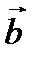 ;
; 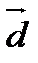 =
= 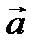 -
- 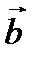 , если
, если 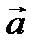 =(-3; 5; 1),
=(-3; 5; 1), 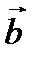 =(4; -2; 8).
=(4; -2; 8).
Решение:
по формулам
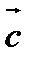 =(х1+х2; у1+у2; z1+z2),
=(х1+х2; у1+у2; z1+z2),
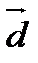 =(x1-x2; y1-y2; z1-z2),
=(x1-x2; y1-y2; z1-z2),
имеем
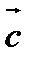 =(-3+4; 5+(-2); 1+8)=(1; 3; 9),
=(-3+4; 5+(-2); 1+8)=(1; 3; 9),
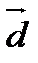 =(-3-4; 5-(-2); 1-8)=(-7; 7; -7).
=(-3-4; 5-(-2); 1-8)=(-7; 7; -7).
Задания для самостоятельного решения:
Вычислить координаты векторов 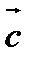 =
= 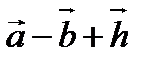 ;
; 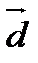 =
= 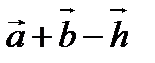 , если
, если 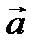 =(4; -3; 10),
=(4; -3; 10), 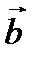 =(-4; 12; -1),
=(-4; 12; -1), 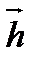 =(3; -7; -11).
=(3; -7; -11).
Контрольные вопросы:
1. Сформулируйте правило треугольника для сложения векторов.
2. Сформулируйте правило параллелограмма для сложения векторов.
3. Запишите формулы сложения (разности) векторов в координат
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|